Journal
of Vectorial Relativity, 2008, Vol. 3, No 3, 30 - 35.
МАССА, ИМПУЛЬС И ЭНЕРГИЯ ГРАВИТАЦИОННОГО ПОЛЯ
С.Г. Федосин
Пермский государственный университет
Вычисляется энергия гравитационного поля и связанная с
ним масса. Определяется импульс гравитационного поля движущегося тела и
соответствующая масса поля. Сравнение данных масс показывает их различие.
Обсуждаются причины нарушения принципа эквивалентности.
Ключевые слова: Гравитация; Энергия поля; Масса поля
PACS: 03.50.Kk ; 04.90.+e ; 95.30
Sf ;
Согласно общей теории относительности (ОТО), энергии
всех видов вносят свой вклад в гравитационную массу тела. В лоренц-инвариантной
теории гравитации (ЛИТГ) плотность гравитационной энергии равна согласно [1],[2]:
![]() , (1)
, (1)
где ![]() – гравитационная
постоянная,
– гравитационная
постоянная,
![]() – гравитационное ускорение,
– гравитационное ускорение,
![]() – скорость
распространения гравитации,
– скорость
распространения гравитации,
![]() – гравитационное
кручение.
– гравитационное
кручение.
Найдём гравитационную энергию ![]() для покоящегося
круглого тела, когда
для покоящегося
круглого тела, когда ![]() . При однородной плотности вещества
. При однородной плотности вещества ![]() для ускорения
для ускорения ![]() внутри и снаружи тела
можно записать:
внутри и снаружи тела
можно записать:
![]() ,
, ![]() ,
,
где ![]() – текущий радиус,
– текущий радиус,
![]() – масса тела.
– масса тела.
Подставляем данные ускорения в (1) и интегрируем по
объёму:
 , (2)
, (2)
здесь ![]() – радиус тела.
– радиус тела.
В (2) основной вклад в гравитационную энергию ![]() даёт энергия поля за
пределами тела. В силу взаимосвязи между массой и энергией следует ожидать, что
энергии (2) соответствует отрицательная
масса:
даёт энергия поля за
пределами тела. В силу взаимосвязи между массой и энергией следует ожидать, что
энергии (2) соответствует отрицательная
масса:
![]() , (3)
, (3)
где ![]() – скорость света.
– скорость света.
За счёт массы ![]() должно происходить
уменьшение гравитационной массы тела по отношению к исходной массе
должно происходить
уменьшение гравитационной массы тела по отношению к исходной массе ![]() .
.
Рассмотрим теперь случай движения тела с постоянной
скоростью ![]() вдоль оси
вдоль оси ![]() . Поскольку тело движется, то
. Поскольку тело движется, то ![]() и существует не равный
нулю вектор плотности импульса гравитационного поля:
и существует не равный
нулю вектор плотности импульса гравитационного поля:
![]() .
(4)
.
(4)
Удобно находить ![]() и
и ![]() через скалярный
через скалярный ![]() и векторный
и векторный ![]() потенциалы
гравитационного поля. В ЛИТГ принято,
что:
потенциалы
гравитационного поля. В ЛИТГ принято,
что:
![]() ,
, ![]() . (5)
. (5)
В свою очередь, потенциалы поля за пределами тела
задаются с учётом запаздывания гравитационного воздействия и потому имеют лоренц-инвариантный
вид:
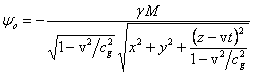 ,
, ![]() . (6)
. (6)
Подставляя (6) в (5), находим:
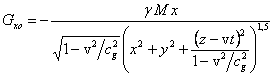 ,
, 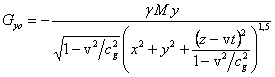 ,
,
 ,
, ![]() ,
, ![]() ,
, ![]() .
.
Видно, что ![]() . Из всех компонент вектора
. Из всех компонент вектора ![]() из (4) важна только одна компонента,
направленная вдоль оси
из (4) важна только одна компонента,
направленная вдоль оси ![]() :
:
![]() . (7)
. (7)
Проинтегрируем ![]() по всем точкам поля в
пространстве за пределами тела в момент времени
по всем точкам поля в
пространстве за пределами тела в момент времени ![]() . Будем считать скорость
. Будем считать скорость ![]() малой, чтобы можно
было пренебречь лоренцевским фактором. Поскольку круглое тело движется, оно
кажется сплющенным в направлении движения и превращается в эллипсоид. В случае
малых скоростей этим изменением формы можно пренебречь. Удобно воспользоваться
сферическими координатами:
малой, чтобы можно
было пренебречь лоренцевским фактором. Поскольку круглое тело движется, оно
кажется сплющенным в направлении движения и превращается в эллипсоид. В случае
малых скоростей этим изменением формы можно пренебречь. Удобно воспользоваться
сферическими координатами:
![]() ,
, ![]() ,
, ![]() .
.
Тогда для импульса поля вне тела имеем:
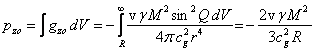 . (8)
. (8)
Внутри тела в системе отсчёта ![]() , связанной с телом, получается следующее:
, связанной с телом, получается следующее:
![]() ,
, ![]() ,
, ![]() ,
,
здесь символом ![]() обозначаются все
величины внутри тела.
обозначаются все
величины внутри тела.
Потенциалы
гравитационного поля ![]() и
и ![]() образуют 4-вектор
образуют 4-вектор 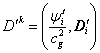 , который можно с помощью матрицы лоренцевского
преобразования
, который можно с помощью матрицы лоренцевского
преобразования ![]() (учитывая ещё движение
тела в нашем случае не вдоль оси
(учитывая ещё движение
тела в нашем случае не вдоль оси ![]() , а вдоль оси
, а вдоль оси ![]() ) перевести в 4-вектор потенциала
) перевести в 4-вектор потенциала ![]() в системе отсчёта
в системе отсчёта ![]() , в которой тело движется со скоростью
, в которой тело движется со скоростью ![]() :
:
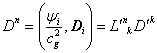 ,
, 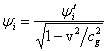 ,
, 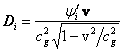 .
.
Как ![]() , так и
, так и ![]() зависят от координат
системы отсчёта
зависят от координат
системы отсчёта ![]() через
через ![]() . Эти координаты можно выразить через координаты системы
отсчёта
. Эти координаты можно выразить через координаты системы
отсчёта ![]() , используя лоренцевские преобразования, и учитывая движение
тела только вдоль оси
, используя лоренцевские преобразования, и учитывая движение
тела только вдоль оси ![]() :
:
![]() ,
, ![]() ,
, 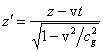 ,
, ![]() .
.
С помощью (5) находим компоненты напряжённостей поля
внутри тела:
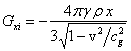 ,
, 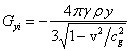 ,
,
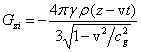 ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для суммарного импульса поля внутри тела вдоль оси ![]() с учётом (4), интегрирования
по объёму тела в начальный момент времени при
с учётом (4), интегрирования
по объёму тела в начальный момент времени при ![]() , и в пределе малых скоростей получается:
, и в пределе малых скоростей получается:
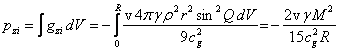 . (9)
. (9)
Сумма импульсов поля внутри и снаружи тела с учётом (2)
и (3) даёт:
![]() , (10)
, (10)
если считать, что ![]() .
.
Коэффициент перед скоростью ![]() в (10) естественно
трактовать как массу передвигающегося гравитационного поля, связанного с телом:
в (10) естественно
трактовать как массу передвигающегося гравитационного поля, связанного с телом:
![]() . (11)
. (11)
Масса поля ![]() по абсолютной величине
оказывается больше, чем масса
по абсолютной величине
оказывается больше, чем масса ![]() гравитационного поля
неподвижного тела.
гравитационного поля
неподвижного тела.
Обсуждение
Поскольку масса поля ![]() входит в импульс
гравитационного поля, то её можно считать инертной массой. Масса поля
входит в импульс
гравитационного поля, то её можно считать инертной массой. Масса поля ![]() связана с энергией
неподвижного потенциального гравитационного поля и относится к гравитационной
массе тела. Неравенство масс
связана с энергией
неподвижного потенциального гравитационного поля и относится к гравитационной
массе тела. Неравенство масс ![]() и
и ![]() означает
неприменимость принципа эквивалентности инертной и гравитационной масс в
отношении массы-энергии гравитационного поля.
означает
неприменимость принципа эквивалентности инертной и гравитационной масс в
отношении массы-энергии гравитационного поля.
С другой стороны, мы уточняем наше понимание
традиционного принципа относительности. Действительно, пока наблюдатель
неподвижен относительно тела, он фиксирует потенциальную энергию
гравитационного поля и соответственно массу поля ![]() . Как только наблюдатель начинает двигаться относительно
тела, он наблюдает изменённую массу тела вследствие наличия импульса тела в его
системе отсчёта. При этом эффективная масса тела плавно зависит от скорости
движения наблюдателя по отношению к телу, что учитывается лоренцевским фактором.
Но ничего такого нет в отношении массы
. Как только наблюдатель начинает двигаться относительно
тела, он наблюдает изменённую массу тела вследствие наличия импульса тела в его
системе отсчёта. При этом эффективная масса тела плавно зависит от скорости
движения наблюдателя по отношению к телу, что учитывается лоренцевским фактором.
Но ничего такого нет в отношении массы ![]() – она сразу
увеличивается в 4/3 раз по отношению к
– она сразу
увеличивается в 4/3 раз по отношению к ![]() . Всё вышесказанное можно повторить и в отношении
массы-энергии электромагнитного поля для тела, имеющего электрический заряд.
. Всё вышесказанное можно повторить и в отношении
массы-энергии электромагнитного поля для тела, имеющего электрический заряд.
Может быть, принцип эквивалентности должен выполняться
только для суммарной массы-энергии тела, включающей в себя энергию покоя его
составных частиц и энергии связи полей? Но тогда мы должны отказаться от
принципа суперпозиции потенциалов поля и его напряжённостей, от возможности
независимого сложения энергий различных видов и соответствующих им масс.
Неравенство масс ![]() и
и ![]() было получено нами на
основе уравнений ЛИТГ. Эти уравнения имеют следующий вид:
было получено нами на
основе уравнений ЛИТГ. Эти уравнения имеют следующий вид:
![]()
![]() (12)
(12)
![]() ,
, ![]() ,
,
где ![]() – вектор напряжённости
гравитационного поля или гравитационное ускорение,
– вектор напряжённости
гравитационного поля или гравитационное ускорение,
![]() – вектор напряжённости кручения
гравитационного поля или просто кручение,
– вектор напряжённости кручения
гравитационного поля или просто кручение,
![]() – гравитационная
постоянная,
– гравитационная
постоянная,
![]() – плотность массы
вещества,
– плотность массы
вещества,
![]() – вектор плотности тока массы, зависящий от скорости движения
– вектор плотности тока массы, зависящий от скорости движения![]() элемента массы.
элемента массы.
Уравнения (12) с точностью до знаков совпадают с
уравнениями Максвелла для электромагнитного поля. Плотность энергии поля в
электромагнетизме равна:
![]() , (13)
, (13)
где ![]() – электрическая
постоянная,
– электрическая
постоянная,
![]() – напряжённость
электрического поля,
– напряжённость
электрического поля,
![]() – индукция магнитного
поля,
– индукция магнитного
поля,
![]() – скорость света.
– скорость света.
Из сравнения (13) и (1) видно, что эти выражения также
имеют одинаковую форму.
Напомним, что в ЛИТГ гравитационное поле является
реальным физическим полем фундаментального типа, аналогичным электромагнитному
полю. Согласно ЛИТГ, ОТО несёт функцию описания явлений в неинерциальных
системах отсчёта. С целью правильного нахождения метрики искривлённого полями
пространства-времени, в уравнения ОТО следует добавлять тензор плотности
энергии-импульса гравитационного поля. Этот тензор определятся в ЛИТГ в
общековариантном виде. Найденная таким образом метрика задаёт не гравитационное
поле, а степень отклонения от плоского пространства-времени Минковского.
Между тем, в стандартной ОТО гравитационное поле
заменяется на метрическое поле, имеющее геометрический смысл. Тогда, быть может
в стандартной ОТО не будет разницы между ![]() и
и ![]() ? Однако, как было уже показано в ряде работ, например в [3],
[4], уравнения ОТО в пределе слабого поля совпадают с уравнениями ЛИТГ (12).
Следовательно, проблема остаётся и в ОТО.
? Однако, как было уже показано в ряде работ, например в [3],
[4], уравнения ОТО в пределе слабого поля совпадают с уравнениями ЛИТГ (12).
Следовательно, проблема остаётся и в ОТО.
По всей видимости, неравенство масс гравитационного
поля не связано ни со специальной теорией относительности, ни с ОТО. Вероятно,
причина скрывается в самой сущности гравитационного поля. Будем считать, что
гравитация между телами создаётся за счёт действия потоков гравитонов. Тот
факт, что для сопутствующего наблюдателя сила гравитации и масса тел не зависят
от их движения с постоянной скоростью относительно потоков гравитонов, мы
фиксируем в виде принципа относительности. В то же время, неравенство масс ![]() и
и ![]() может отражать тот
факт, что в инертной массе
может отражать тот
факт, что в инертной массе ![]() содержится
дополнительная масса поля. Эта дополнительная отрицательная масса, согласно (11)
равная
содержится
дополнительная масса поля. Эта дополнительная отрицательная масса, согласно (11)
равная ![]() , связана с движением тела. Она может представлять собой массу
энергии возбуждения гравитационного поля, которая необходима, чтобы перевести
тело из одного состояния относительно потоков гравитонов или относительно
наблюдателя, в другое состояние движения.
, связана с движением тела. Она может представлять собой массу
энергии возбуждения гравитационного поля, которая необходима, чтобы перевести
тело из одного состояния относительно потоков гравитонов или относительно
наблюдателя, в другое состояние движения.
Заметим, что при выводе соотношения между массами ![]() и
и ![]() мы не уточняли
первоначальное состояние тела. В силу принципа относительности, для
вычисления
мы не уточняли
первоначальное состояние тела. В силу принципа относительности, для
вычисления ![]() было несущественно, находится
ли тело в покое относительно изотропной системы отсчёта потоков гравитонов или
движется вместе с наблюдателем относительно этой системы отсчёта. Но с точки
зрения теории гравитации, основанной на концепции гравитонов, это важно. Ведь
при движении тела или наблюдателя относительно потоков гравитонов эти потоки
становятся неизотропными, что и может стать причиной как появления импульса
гравитационного поля, так и дополнительной массы поля
было несущественно, находится
ли тело в покое относительно изотропной системы отсчёта потоков гравитонов или
движется вместе с наблюдателем относительно этой системы отсчёта. Но с точки
зрения теории гравитации, основанной на концепции гравитонов, это важно. Ведь
при движении тела или наблюдателя относительно потоков гравитонов эти потоки
становятся неизотропными, что и может стать причиной как появления импульса
гравитационного поля, так и дополнительной массы поля ![]() . При этом для наблюдателя, покоящегося относительно тела,
дополнительная масса поля
. При этом для наблюдателя, покоящегося относительно тела,
дополнительная масса поля ![]() из уравнений поля не
находится (это следствие принципа относительности). Из изложенного следует, что
различие инертной и гравитационной масс гравитационного поля может быть
объяснено существованием выделенной изотропной системы отсчёта. Особенностью
такой системы отсчёта тогда является изотропность потоков гравитонов,
ответственных за гравитацию.
из уравнений поля не
находится (это следствие принципа относительности). Из изложенного следует, что
различие инертной и гравитационной масс гравитационного поля может быть
объяснено существованием выделенной изотропной системы отсчёта. Особенностью
такой системы отсчёта тогда является изотропность потоков гравитонов,
ответственных за гравитацию.
Литература
1. С.Г. Федосин. Физика и философия подобия от преонов до
метагалактик. – Пермь: Стиль-МГ, 1999 – 544 с.
2. S.G. Fedosin. Electromagnetic and Gravitational Pictures of the World. // Apeiron, Vol. 14, No. 4, P. 385-413, 2007.
3.
M. Agop, C. Gh. Buzea and B. Ciobanu. On Gravitational
Shielding in Electromagnetic Fields. – arXiv: physics / 9911011 v1,
4.
R.P. Lano. Gravitational Meissner Effect. – arXiv:
hep-th/9603077 v1,
MASS, MOMENTUM AND ENERGY OF
GRAVITATIONAL FIELD
The energy of the
gravitational field and the mass related to it are calculated. The momentum of
the gravitational field of a moving body and the appropriate mass of the field
are determined. Comparison of the given masses shows their difference. The
reasons of violation of equivalence principle are discussed.
Источник:
http://sergf.ru/mas.htm