International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp.
12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12
Equations of motion in the theory
of relativistic vector fields
Sergey G. Fedosin
PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia
E-mail: fedosin@hotmail.com
Within the
framework of the theory of relativistic vector fields, the covariant
expressions are presented for the equations of motion of the matter and the
field. These expressions can be written either in terms of the field tensors,
that is, the fields’ strengths and solenoidal vectors, or in terms the
four-potentials, that is, the fields’ scalar and vector potentials. This state
of things is due to the fact that the Lagrange function initially implied the
complementarity of description in terms of the strengths and the field
potentials. It is shown that the equation for the fields, obtained by taking
the covariant derivative in the equation for the metric, has a deeper meaning
than the ordinary equation of motion of the matter, found with the help of the
principle of least action. In particular, the above-mentioned equation for the
fields leads to the generalized Poynting theorem, and after integration over
the volume it allows us to introduce for consideration the integral vector as a
measure of the energy and the fields’ energy fluxes, associated with a system
of particles and fields.
Keywords: vector field; equation of motion; field equations.
1. Introduction
One of the most
effective ways of obtaining the equations of motion is to apply the principle
of least action [1-3]. In this case, as a rule, either
the motion of charged particles in an electromagnetic field or the motion of
particles in a potential field or in a scalar pressure field are described. As
for the gravitational field, it usually appears as a tensor field within the
framework of the general theory of relativity, including the use of modified
versions of this theory to describe the dynamic properties of matter [4-6].
The concept of
the electromagnetic field, which is a vector field, is successfully used in
science and technology for a comprehensive description of electromagnetic phenomena.
It is also possible to represent all the fields acting in macroscopic systems
as the corresponding vector fields [7-9]. This allows us to apply the well-developed mathematical apparatus of
the theory of relativistic vector fields and to describe with its help both the
equation of the matter’s motion under the action of the fields and the
propagation of the fields during the matter’s motion.
The main
purpose of this paper is to present the equations of motion of the matter and
field in a covariant form, which is suitable for use, in particular, in the
curved spacetime and in any reference frames. We will systematize the results
presented in the previous papers and will supplement them with regard to the
equations for the fields’ scalar and vector potentials.
Among a great
number of vector fields, only the four fields will be considered, including the
electromagnetic field, gravitation within the covariant theory of gravitation
[10], the acceleration field and the vector pressure field [11]. Other macroscopic
vector fields can be easily added to the presented equations, as has already
been done for the dissipation field [12] and the fields of strong and weak
interactions [13].
In our
calculations, we will use everywhere the metric signature of the form (+,–,–,–).
2. The
general forms of the equation of motion
The application
of the principle of least action, taking into account the energy gauge by means
of the cosmological constant within the framework of the covariant theory of
gravitation and the four vector fields, leads to the equation for finding the
metric tensor components [14]:
, (1)
where 
is the Ricci tensor; 
is the scalar curvature; 
is the metric tensor; 
is the speed of light, 
, where 
is the gravitational constant; 
is a certain coefficient of the order of unity
to be determined; 
, 
, 
and 
are the stress-energy tensors
of the gravitational and electromagnetic fields, the acceleration field and the
pressure field, respectively.
With the help
of the covariant derivative 
we can find the
four-divergence of both parts of (1). The divergence of the left-hand side is
equal to zero due to the equality to zero of the Einstein tensor’s divergence, 
, and also as a consequence of the fact that outside the body the scalar
curvature vanishes, 
, and inside the body it is considered to be a constant. The latter
follows from the gauge condition of the system’s energy [14]. The divergence of
the right-hand side of (1) is also equal to zero:
. (2)
Expression (2)
for the space components of the tensors with the index 
shows that the
change over time of the fields’ energy fluxes leads to the so-called fields’
tensions. As for the time components of the tensors with the index 
, for them (2) is the expression of the generalized
Poynting theorem for all the fields, both inside and outside the matter, that
determines the energy balance in the system.
The
stress-energy tensors of the gravitational field [10], [15], the
electromagnetic field, the acceleration field and the pressure field [11],
[14], presented in (2), are derived from the principle of least action:
,
.
,
. (3)
Here 
, 
, 
and 
represent the gravitational tensor,
electromagnetic tensor, acceleration tensor and pressure field tensor,
respectively; 
is the electric constant, 
is the acceleration field coefficient; 
is the pressure field coefficient.
All
the tensors in (2) and in (3) are expressed in terms of the corresponding
fields’ strengths and solenoidal vectors. For example, the electromagnetic
tensor and the stress-energy tensor of the
electromagnetic field 
are expressed in terms of the field strength 
and the magnetic field 
.
Equation
(2) inside the matter can be transformed in such a way that the field tensors
themselves would appear in it instead of the stress-energy tensors. In
particular, we can prove the following equalities [15, 16]:
, 
,
, 
. (4)
In
order to prove the validity of (4), it is necessary to substitute (3) into (4),
to apply the covariant derivatives to the products of the field tensors, and then
to use the equations of the respective field, so that the mass four-current 
and the charge four-current 
would appear in (4).
In view of (4), equation (2) inside the matter
turns into the equation of motion and takes the following form:
. (5)
The
equation of motion in the form of (5) can also be obtained directly from the
principle of least action [15], regardless of (1) and (2).
In order to reduce (5) to a more convenient form,
we should take into account the expression for the mass current 
in terms of the invariant
mass density 
and the four-velocity 
of the particles, as well as the definition of
the acceleration tensor 
, where 
is the four-potential of the acceleration
field. With this in mind, we have the following:
. (6)
In
this case, the operator of proper-time-derivative 
was used, where 
is the symbol of the four-differential in the
curved spacetime, 
is the proper time [10]. The substitution of
(6) into (5) gives the following:
. (7)
If other vector
fields are taken into account in the system, such as the dissipation field [12]
or the macroscopic vector fields of strong and weak interactions [13], then the
respective additional terms with the tensors of these fields appear on the
right-hand side of (7).
For an
arbitrary vector 
we can write:
, 
, (8)
where 
is the Christoffel symbol.
Replacement of 
by the
four-potential of the acceleration field 
in (8) gives
the following:
, 
. (9)
Let us
substitute both equalities (9) into (7):
. (10)
We will divide
equation (10) into two equations, one for the time components and the other for
the space vector components, with the index 
:
.
. (11)
In (11),
differentiation with respect to the proper time can be replaced
by differentiation with respect to the coordinate time 
as follows: 
. In this case, for the mass four-current and for the
charge four-current 
, we can write:
, 
, (12)
where 
is the invariant charge density, 
is the velocity of the matter
particles’ motion. In the Cartesian space coordinates,
the four-dimensional quantity 
is expressed in
terms of the speed of light and the components of the particles’ velocity.
Also taking
into account that the field tensors in (11) are expressed in terms of the
strengths and solenoidal vectors, and the four-potential of the acceleration
field 
is defined by
the scalar potential 
and the vector
potential 
, in view of (12), we find the following:
.
, (13)
where 
, 
and 
denote the
strengths of the gravitational field, electromagnetic field and pressure field,
respectively; and, similarly, 
is the gravitational torsion field; 
is the magnetic induction, and 
is the solenoidal vector of the
pressure field.
According to
the definition of the acceleration field tensor, its components include the
strength 
and the
solenoidal vector 
, expressed in terms of the acceleration field potentials:
, 
.
The vectors 
and can be included
in equations (13). To do this, on the left-hand side of (13) we must take into
account the operator equation 
, and on the right-hand side of (13) we must expand
the products of the four-vectors into their components, taking into account the
definitions 
and 
:
.
.
With this in
mind, it follows from (13):
.
. (14)
If in (14) we
multiply scalarly the second equation by the velocity 
, we will obtain the first equation in (14).
Equations (10),
(11), (13) and (14), written in a covariant way, do not contain Christoffel
symbols, which simplifies the solution of these equations. We should note that
equations (14) are completely symmetric with respect to all the four vector
fields. This means that, for example, if the field strengths and the velocity 
of the system’s
typical particles are known as functions of time and coordinates, then from the
first equation (14) we can find the relationship between the field
coefficients, that is, between 
, 
, 
and 
.
3. Rectilinear
motion of an ideal solid body
An ideal solid
body can be considered as the limiting case of the relativistic uniform system,
in which the system’s particles are fixed relative to each other. This means
that the Lorentz factor 
of the
particles is equal to 1, and the velocity 
of their motion
is equal to zero in the body’s center-of-momentum frame.
This fact
allows us to substantially simplify the equation of motion of the body.
We will start
with the definition of the four-potential of the acceleration field of an
arbitrary physical system. According to [11], the four-potential of any vector
field, the vector potential of which is equal to zero in its proper reference
frame, that is, in the center-of-momentum frame, in case of rectilinear motion
in the laboratory reference frame can be represented by the formula:
,
(15)
where
for the electromagnetic field and 
for the other fields; 
is the invariant energy density of the
interaction between the field’s four-potential and the corresponding
four-current; 
is the four-velocity with a covariant index
that specifies the motion of the center of momentum of the physical system in
the laboratory reference frame.
In the proper reference frame 
, and
the vector potential as the space component of 
vanishes according to (15). However, some
physical systems, even if they have their own center of momentum fixed, have
not only a scalar field potential but also a vector field potential within the
system. Therefore, a more general expression for the field’s four-potential in
the laboratory reference frame is as follows:
,
(16)
where
is a
matrix connecting the coordinates and time of the two reference frames, one of
which is laboratory reference frame and the other moves together with the center
of momentum of the physical system under consideration, so that there is the
field’s four-potential 
in it. In the special case of
the system’s motion at the constant velocity the matrix represents the Lorentz transformation matrix
[10].
Let us now assume the simplest case, when the
physical system in the form of a sphere has no general rotation, the typical
particles of the system move randomly and they also have neither proper
rotation nor their own vector potentials in the particles’ center-of-momentum frames.
In this case, we can use a simpler formula (15) instead of (16) to determine
the four-potential of the acceleration field in case of rectilinear motion.
In a fixed sphere, the energy density in the
volume of each particle 
,
and, according to (15), for the acceleration field, when the sphere moves in
the laboratory reference frame, the four-potential will equal 
. This means
that if for an observer inside the sphere with particles, within the framework
of the relativistic uniform model, the quantity 
is an invariantly defined Lorentz factor as a
certain function of coordinates and time, then for an observer in the
laboratory reference frame, in which the center of the sphere has the
four-velocity 
, the
four-potential of the acceleration field for each point inside the moving
sphere will equal 
.
By definition, the four-potential of the
acceleration field is the four-vector 
,
where 
and 
denote the scalar and vector potentials,
respectively. Taking into account (15) and the relation 
, it turns
out that in the relativistic uniform system in the form of a fixed sphere the
scalar potential will be 
. As for the
global vector potential of the acceleration field 
, it will
differ from zero only in the systems with directed fluxes of particles.
In the ideal case, when the system of particles
is not a rotating perfectly solid body and the particles inside the system are
motionless, it must be 
, and
then the four-potential of the acceleration field would coincide with the
four-velocity of the system’s center of momentum, 
.A material
point represents a miniature physical system, and if we do not go deeply into
the structure of the internal motion of its matter and if we consider this
point as a solid body, then the four-potential of the acceleration field of
such a point will also be equal to the four-velocity of its motion.
Thus, in case of rectilinear motion of an ideal
solid body in the absence of rotation, in equation of motion (7) the
four-potential of the acceleration field 
can be replaced by the four-velocity of the
body’s center of momentum 
. Taking
into account the relation 
, which
follows from the equality 
, instead of
(7) we obtain the following:
. (17)
On the
left-hand side of (17) there is the covariant four-acceleration 
, and on the right-hand side there is the sum of the
densities of the gravitational and electromagnetic forces and the density of
the pressure force. In particular, the expression 
defines the
density of the electromagnetic Lorentz force. Equations (10) and (11), in view
the relation 
, are written as follows:
.
, 
. (18)
On the left-hand
side of (18) we will use the expression for the four-velocity 
, and on the right-hand side we will express the field
tensors in terms of the strengths and solenoidal vectors.
Then, in view
of (12), equation (18) can be transformed as follows:
,
. (19)
In the flat
Minkowski spacetime 
, where 
is the Lorentz factor, the
Christoffel symbols vanish, and the metric tensor 
transforms into the metric tensor 
,
which is
independent of time and coordinates and has only the diagonal components. As a
result, equations (19) are also simplified:
,
(20)
. (21)
The
three-dimensional acceleration vector of a solid body or a particle is 
, so that 
. Substituting here the expression 
from (20) and
comparing with (21), we obtain the equation for the acceleration in the
framework of the special theory of relativity, expressed in terms of the
fields’ strengths and solenoidal vectors:
. (22)
If we denote
the force density as
,
then (20-22)
can be rewritten as follows:
, 
, 
.
The relativistic
energy and momentum of the solid body with the mass 
and charge 
are given by
the expressions 
, 
. Let us assume that the mass and charge of the body
are constant in motion. Then after multiplying equations (20) and (21) by the
mass , we can introduce the force 
and represent
the equations as follows:
,
.
In the general
case, the fields inside a solid body are non-uniform and differ in value at
different points. In this case, the body can be divided into 
parts with the masses 
, where the index 
ranges from 0
to . Multiplying equations (20) and (21) by 
, 
…, , then summing the equations, and passing from the
sums to the integrals over the whole body, we arrive at the following:
,
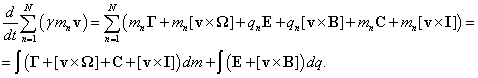
Comparison with
the previous equations gives the following:
, 
, 
,
.
In these
relations it is taken into account that in case of rectilinear motion of a
solid body without rotation of this body, the velocity 
and the Lorentz
factor 
are constant
for all the points of the body.
The case is
possible when the body does not rotate in the center-of-momentum frame, but it
does not move along a straight line. This leads to the fact that the body
rotates relative to the point located at the instantaneous radius of curvature
of the motion trajectory, and then the velocities of the points inside the body
become different. In this case, the motion of the body’s points should be
described by more general equations (14).
4.
Expression of the equation of motion in terms of the fields’ four-potentials
By definition,
the field tensors are expressed in terms of the four-curl applied to the
fields’ four-potentials. For the acceleration field, gravitational and electromagnetic
fields and pressure field, this gives the following:
, 
,
, 
, (23)
where 
is the four-potential of the acceleration
field, 
and 
denote the scalar and vector potentials,
respectively,
is the four-potential
of the gravitational field, described in terms of the scalar potential 
and the vector
potential 
of this field,
is the four-potential
of the electromagnetic field, given by the scalar potential 
and the vector
potential 
of this field,
is the four-potential
of the pressure field, containing the scalar potential 
and the vector
potential 
.
Let us
substitute (23) into (7), taking into account the expressions for the mass
current 
and for the
charge current 
, and also taking into account rule (8) for the
operator of the proper-time-derivative. We will also use the expression for the
covariant derivative for the arbitrary four-vector 
:
.
All this gives
the following equation:
. (24)
Equation of
motion (24) falls into two equations, since it can be written separately for
the time and space vector components of the fields’ four-potentials. Using the
expression 
for the time
component of the partial derivative, we have:
,
. (25)
In (25) the
three-dimensional spatial gradient operator in Cartesian coordinates has the
components 
, while the index 
in 
defines the
components, which correspond to the components 
, 
, 
and 
of the vector field potentials.
The peculiarity
of the covariant equations of motion (24) and (25) is the fact that they are
fully expressed in terms of the fields’ four-potentials or in terms of their
components in the form of the fields’ scalar and vector potentials. It is to be
recalled that, in contrast, the equations of motion in the form of (7), (10)
and (11) are expressed in terms of tensors, that is, in terms of the fields’ strengths
and solenoidal vectors, as was shown in (13) and (14).
We will use the
relation 
in equations
(25). This gives the following:
, (26)
. (27)
For the case of
rectilinear motion of an ideal solid body without rotation, the four-potential 
of the acceleration field at each
point of the body coincides with the four-velocity 
of motion of
the body’s center of momentum. In this case in (25), (26) and (27) we will have
, 
.
In the Minkowski
spacetime and the equations of motion of a solid
body are further simplified, since then in (26) and (27) 
, 
, 
. In addition, since 
, the following relations hold true:
,
.
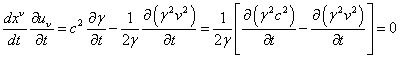Taking this
into account, instead of (26) and (27) we can write the following:
, (28)
. (29)
5.
Complementarity of description in terms of the potentials and field strengths
We will
demonstrate the equivalence of equations of motion (26), (27) and equations
(14). For this we will need expressions (23) written in a covariant vector
form. The field tensors’ components according to (23) are the strengths and
solenoidal vectors, which by definition depend on the time and space
derivatives of the corresponding scalar and vector potentials:
, 
, 
, 
,
, 
, 
, 
. (30)
We will use the
operator equation 
on the
left-hand side of equation (26), and on the right-hand side of (26), in view of
the definitions 
and 
, we will expand the products of the four-vectors into their components, so we
will obtain, for example, the following:
.
Transforming also
the remaining terms on the right-hand side of (26), we arrive at the following:
.
Now we can take
into account (30):
.
This equality
coincides with the first equality in (14).
Taking now the Cartesian
coordinates for simplifying, we will project all the terms in (27) onto the
axis 
, so that in the equation we will have 
, 
:
. (31)
In view of
(30), we will expand the products of the four-vectors into their components on
the right-hand side of (31):
, 
,
.
Substitution of
all this into (31) gives the following:
.
This equation
coincides with the projection of the second equation in (14) onto the axis . Thus, equations of motion (26) and (27) are
equivalent to equations (14), which is a consequence of the relation between
the strengths and the field potentials in (30).
In addition to
the presence of proper equations of motion, the complementarity of the
potentials and the field strengths is emphasized by the fact that for them
there are proper field equations. Thus, for the four fields used here, the
field equations for determining the strengths and the solenoidal vectors have
the following form [14]:
, 
,
,
,
, 
,
, 
. (32)
In
the first equations in (32), the field tensors can be replaced by their
expressions in terms of the four-potentials according to (23). After this, we
should use the rule for the difference of the second-order covariant
derivatives of the arbitrary four-vector 
:
.
where 
is the Ricci
tensor with the mixed indices.
With this in mind,
we arrive at the field equations for the four-potentials of the fields:
, 
.
, 
.
(33)
As a rule, the
four-potentials of the fields are gauged in such a way that their covariant
divergences are equal to zero:
, 
, 
, 
. (34)
The use of (34)
leads to simplification of (33):
, 
.
, 
. (35)
It is
interesting that the equations with the d'Alembertian 
can be obtained
not only for the four-potentials, but also for the field tensors themselves.
The derivation of one such equation is shown in Appendix A using the example of
the electromagnetic field equations in (25). According to the relation (A10),
we obtain the following:
.
Similarly, we
can write for the tensors of the gravitational field, the acceleration field
and the pressure field:
,
,
. (36)
Equations (36)
represent the wave equations for the field tensors in the curved spacetime.
In the
Minkowski spacetime, the covariant derivative becomes a four-gradient, the
covariant d'Alembertian 
is transformed into the ordinary
d'Alembertian 
, the Ricci tensor 
and the
curvature tensor 
vanish.
In this case,
equations (32) can be presented as the equations for determining the fields’
strengths and the solenoidal vectors:
, 
, 
, 
.
, 
, 
, 
.
, 
, 
, 
.
, 
, 
, 
. (37)
In (37) 
is the electric current density, 
is the Lorentz
factor, 
is the invariant
charge density, 
is the velocity of
motion of the matter’s particles, and 
is the mass current
density.
In this case,
equations (35) turn into the wave equations for the four-potentials in the
framework of the special theory of relativity. We can expand these equations
and write them separately for the scalar and vector potentials:
, 
,
, 
,
, 
,
, 
. (38)
The
inhomogeneous wave equations (36) for the field tensors are also simplified,
because the terms with curvature vanish. Since the tensor components are
expressed in terms of the fields’ strength vectors and the fields’ solenoidal
vectors, the wave equations can be written for each such vector:
, 
,
, 
,
, 
,
, 
. (39)
It follows from
(38) and (39) that in the empty space, where there are no charges and currents
and therefore 
, 
, the following relations must hold for the field
potentials, the electric field strength and the magnetic field of the
electromagnetic wave: 
, 
, 
, 
. The similar relations in the empty space, in the
absence of matter and its fluxes, must also be valid for the gravitational
field in the framework of the covariant theory of gravitation: 
, 
, 
, 
.
Although
equations (37) are of the first order, they are vector equations and for each
field they contain four separate coupled equations for the corresponding
strengths and solenoidal vectors, which makes it difficult to solve them. In contrast,
the solutions of equations (38) for the potentials have a standard form and are
called solutions with retarded potentials. As a result, we can substitute the
potentials found from (38) into the equations of rectilinear motion of the
solid body (28) and (29), and we can determine the Lorentz factor 
and the
velocity 
as functions of
the time and coordinates in the Minkowski spacetime. In practice, however, it
usually happens in a different way: first, using the potentials found, with the
help of (30) the fields’ strengths and solenoidal vectors are calculated, and
then they are substituted into the equations of rectilinear motion of the solid
body (20), (21), and (22).
Since the components
of the field tensors become known, they can be used to calculate the
stress-energy tensors of the fields in (3).
6.
Conclusion
However, the meaning of equation (2) is much broader
and it does not reduce only to the equation of motion. Indeed, equation (2) is
valid for the space outside the matter’s limits, defining there the balance of
the fields’ energy in accordance with the generalized Poynting theorem, as well
as the corresponding field strengths in the space created by the energy fluxes.
Moreover, equation (2) in the limit of the weak field and low velocities, where
the effects of spacetime curvature can be neglected, can be integrated over the
four-volume. The subsequent application of the divergence theorem reduces
integration over the four-volume to integration of the time components of the
fields’ total stress-energy tensor over the three-volume, if the instantaneous
situation is considered at a certain given time point. This leads to the
determination of the integral vector, which is conserved in closed systems. In
contrast, the equation of motion of the matter in the form of (5) cannot be
integrated over the volume and does not result in the integral vector.
The equations of motion are simplified for the ideal
solid body that does not rotate in its proper center-of-momentum frame and
moves rectilinearly, parallel to itself. In order to describe such a motion, we
can apply equations (17) and (18), where the field tensors are used, and
equations (19) with the fields’ strengths and solenoidal vectors. In the flat
Minkowski spacetime, the equations of motion are even more simplified and can
be represented in the form of equations (20), (21) and (22), which show the
rate of change of the energy density and the momentum density, respectively,
depending on the value of the strengths and solenoidal vectors inside the
matter.
In Section 4, the equation of motion in the form of
(24-27) was fully expressed in terms of the derivatives of the fields’ scalar
and vector potentials taken with respect to time and coordinates. For the
rectilinear motion of the solid body in the flat Minkowski spacetime, the
equation of motion can be written in the form of two equations (28) and (29),
equivalent to equations (20) and (21).
The fact that equations of motion (26) and (27)
coincide with equations (14) can be proved using the definitions of the
strengths and solenoidal vectors in terms of the fields’ scalar and vector
potentials indicated in (30). We provided this proof in Section 5.
Due to the relationship between the strengths and
solenoidal vectors on the one hand, and the fields’ scalar and vector
potentials on the other hand, field equations (32) for the strengths and
solenoidal vectors can be transformed into wave equations (35) for the fields’
scalar and vector potentials. For the field tensors, we also obtained wave
equations (36) in the curved spacetime. For all these equations, we provided
their expressions in the framework of the special theory of relativity.
Thus, the mutual complementarity of the field
strengths and field potentials is manifested not only in case of their presence
in the Lagrange function and their participation in the equation of motion, but
also in the corresponding equations for the fields themselves.
If we know the dependences of the mass density 
and the charge density 
, as well as the four-velocity 
of the matter’s motion at each
point of the system at any time, this is enough to determine all the
characteristics of the system. Indeed, first we find the mass four-current 
and the charge four-current 
, and then, using the equations of the corresponding fields, we
calculate the field tensors, as well as the four-potentials of the fields.
After that, we can find the stress-energy tensors of the fields, the system’s
metric, the densities of the four-forces, we can solve the equation of motion
and also calculate the energy, momentum, angular momentum, and the integral
vector of the system’s fields, which is associated with the fields’ energy
fluxes and is found by integrating equation (2) over the four-volume. In addition, we can also determine the four-acceleration of the matter
as the derivative of the four-velocity with respect to the proper time in the
curved spacetime:
.
The solution of inverse problems, in which, for
example, the dependence of the four-velocity of the matter is unknown, but the
fields’ distribution as well as the distribution of mass and charge are
specified, can be more difficult. In this case, first it is necessary to
reestablish the dependence of the four-velocity of the matter with the help of
the field equations, and then to determine the remaining characteristics of the
system, including the four-acceleration.
References
1. Landau L.D. and Lifshitz
E.M. Mechanics, 3-rd edition. Pergamon, Oxford (1974).
2. José J.V. and Saletan
E.J. Classical dynamics: a contemporary approach. Cambridge University Press
(1998).
3. Goldstein H. Classical mechanics, 2-nd
edition. Addison-Wesley, Reading (1981).
4. Yousaf Z. Spherical relativistic vacuum core models in a Λ-dominated era.
Eur. Phys. J. Plus, Vol.
132, 71 (2017). doi:10.1140/epjp/i2017-11336-9.
5. Yousaf Z. Stellar filaments with Minkowskian
core in the Einstein-Λ gravity. Eur. Phys. J. Plus, Vol. 132,
276 (2017). doi:10.1140/epjp/i2017-11547-0.
6. Yousaf Z. Structure scalars of spherically symmetric dissipative fluids
with f(G,T) gravity. Astrophys. Space Sci., Vol. 363,
226 (2018). doi:10.1007/s10509-018-3450-7.
7. Fedosin S.G. Estimation of the physical parameters of planets and
stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol.
94, No. 4, pp. 370-379 (2016). doi:10.1139/cjp-2015-0593.
8. Fedosin S.G. Two components of the
macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1,
No. 2, 1750002, 9 pages (2017). doi:10.1142/S2424942417500025.
9. Fedosin S.G. The virial theorem and the kinetic energy of particles
of a macroscopic system in the general field concept. Continuum Mechanics and
Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2016). doi:10.1007/s00161-016-0536-8.
10.
Fedosin S. The
physical theories and infinite hierarchical nesting of matter,
Volume 2, LAP LAMBERT Academic Publishing, pages: 420, ISBN-13:
978-3-659-71511-2. (2015).
11. Fedosin S.G.
The procedure of finding the
stress-energy tensor and vector field equations of any form. Advanced
Studies in Theoretical Physics, Vol. 8, pp. 771-779 (2014). doi:10.12988/astp.2014.47101.
12. Fedosin S.G.
Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid
with Regard to the Acceleration Field, Pressure Field and Dissipation Field.
International Journal of Thermodynamics, Vol. 18, No. 1, pp. 13-24, (2015). doi:10.5541/ijot.5000034003.
13.
Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. doi:10.4236/oalib.1102459.
14. Fedosin S.G. About the
cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30
(2016}. doi:10.5281/zenodo.889304.
15. Fedosin S.G. The Principle of Least Action in Covariant Theory of
Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). doi:10.5281/zenodo.889804.
16. Fock V. A. The Theory of Space,
Time and Gravitation.
Pergamon Press, London. (1959).
Appendix A. Derivation of the covariant wave
equation for the electromagnetic field tensor
The covariant
equations of the electromagnetic field for the electromagnetic tensor 
have the
following form:
, 
, (A1)
where 
is the magnetic constant, 
is the charge four-current.
Let us take in
(A1) the second equation without the field sources, and apply the covariant
derivative 
to it:
. (A2)
Next, we will
use the rule for the difference of the second-order covariant derivatives:
,
where 
is the curvature tensor.
In view of this
rule, we find:
. (A3)
. (A4)
Now we will
take into account the first equation of the electromagnetic field from (A1) and
the antisymmetry of the electromagnetic tensor:
, 
.
Consequently,
in (A3) and (A4) we will have the following:
, 
. (A5)
For the
curvature tensor, there is a rule:
.
After
multiplying this equality by 
we obtain the following:
.
Here if we
assume that index 
, then the following relation will be valid:
. (A6)
With this in
mind, the second term on the right-hand side of (A3) and the third term on the
right-hand side of (A4) are transformed as follows:
, 
. (A7)
Let us transform
the third term on the right-hand side of (A3) and the second term on the
right-hand side of (A4), in the latter case we will apply the operation of
permutation of the indices 
and 
:
,
(A8)
In view of
(A5), (A7) and (A8), for the sum of (A3) and (A4) in (A2) we find the
following:
. (A9)
The last term
on the right-hand side of (A9) can also be transformed:
In this case
for the curvature tensor we applied the rule
,
used the
operation of permutation of the indices 
and 
in one of the
tensor products, and took into account the antisymmetry of the electromagnetic
tensor 
, as well as the antisymmetry of the curvature tensor
in case of permutation of the adjacent indices in each pair of indices.
Finally, we
obtain the following:
. (A10)
In (A10), the
scalar operator 
represents the four-dimensional d'Alembertian in the
curved spacetime.
Source: http://sergf.ru/eqen.htm