Canadian Journal
of Physics, Vol. 92, No. 10, P. 1074 – 1081 (2014). http://dx.doi.org/10.1139/cjp-2013-0683
Energy, Momentum, Mass and
Velocity of a Moving Body in the Light of Gravitomagnetic Theory
Sergey G. Fedosin
Sviazeva Str., 22-79, Perm 614088, Perm Region,
Russia
Email:
intelli@list.ru
Abstract : In
the weak-field approximation of the covariant theory of gravitation the 4/3
problem is formulated for internal and external gravitational fields of a body
in the form of a uniform ball. The dependence of the energy and the mass of the
moving body on the energy of the field accompanying the body, as well as the
dependence on the characteristic size of the body are described. Additions in
the energy and the momentum of the system, defined by
the energy and momentum of the gravitational and electromagnetic fields,
associated with the body, are explicitly calculated. The conclusion is made
that the energy and the mass of the system can be described through the energy
of ordinary and strong gravitation and through the energies of electromagnetic
fields of particles that compose the body.
Key words: Energy; Momentum; Theory of Relativity; Gravitation; Field
Potentials; Gravitomagnetism.
PACS: 03.20.+i, 03.50.x,
12.10.-g
1.
INTRODUCTION
In
relativistic mechanics, there are standard formulas for the dependence of
energy and momentum of a particle with the mass 
on its velocity 
:
, 
, (1)
where 
.
If
the energy 
and momentum 
in Eq. (1) are known the mass and the velocity
of the particle can be calculated:
,
. (2)
In Eqs. (1) and
(2) the speed of light 
is included. For a particle in rest velocity
and momentum are zero, and the energy of the particle equals the rest energy:
.
(3)
Equation
(3) reflects the principle of proportionality of mass and energy. In elementary
particle physics the energy and the momentum are usually measured parameters,
and the mass and the velocity are found from Eq. (2) and are secondary
parameters.
Now,
we shall suppose that the measured parameters are the energy and the velocity
of the particle. In this case, from Eqs.
(1) and (3) we can calculate the mass and momentum:
, 
. (4)
The
case is also possible when the measured parameters are the momentum and the
velocity of the particle and the calculated quantities are the mass and energy:
, 
. (5)
If
the particle velocity 
is given, then the mass can be found either
through the energy according to Eq. (4), or through
the momentum according to Eq. (5), in both cases, the mass should be the same.
From
the above formulas it is not clear whether they contain the energy and the
momentum of fields, which are inherent in the particles and the test bodies. In
particular, the test bodies always have their proper gravitational field and
can also carry an electrical charge and the corresponding electromagnetic field.
In general theory of relativity (GTR) it is considered that
relativistic energy and mass of a body decrease due to the contribution of
gravitational energy. Although in GTR there is no unique definition of the
gravitational energy and its contribution to the integral energy [1], in the
weak-field approximation the following is assumed [2]:
, 
. (6)
where 
is the relativistic energy of system in the
gravitational field, is the energy in the absence of the field, 
is the potential gravitational energy of the
body.
Since
the energy is negative, then according to GTR the mass 
as the mass of the system consisting of the
body and its fields should decrease with increasing of the field.
The
main purpose of this paper is to incorporate explicitly in the relativistic
formulas for the energy and the momentum the additives, resulting from the
energy and the momentum of fields associated with the test bodies. All
subsequent calculations will be made in the framework of the covariant theory
of gravitation (CTG) [3]. We will apply the weak-field approximation, when CTG
is transformed into the Lorentz-invariant theory of gravitation (LITG), and it
becomes possible to compare our results with the formulas of GTR in gravitomagnetic approximation.
2. 4/3 PROBLEM FOR ENERGY – MOMENTUM OF THE INTERNAL AND EXTERNAL
ELECTROMAGNETIC FIELD OF THE CHARGED HEAVISIDE ELLIPSOID
When the
spherical charge 
with the
radius 
is moving at
the velocity 
in empty
space, its shape becomes according to the special theory of relativity an
oblate ellipsoid. In this case, one axis of the ellipsoid, which is directed
along the velocity of motion becomes shorter and equals 
, where 
. Such an ellipsoid is called the Heaviside
ellipsoid.
2.1. External Electromagnetic Field
The scalar
and vector potentials 
, the electric field strength and the magnetic
induction 
of a
uniformly moving charge, the electromagnetic energy 
and the
momentum 
of the field
outside the charged ellipsoid, the electromagnetic energy 
and the
momentum 
of the field
inside a uniformly charged ellipsoid, other electromagnetic quantities in the
case of the Heaviside ellipsoid are well studied. Relations of the special
theory of relativity allow us to determine the relationship between the quantities
for a resting spherical charge and the corresponding quantities for a moving
charge.
From
Heaviside’s works [4, 5] we know that if the center of a charged ellipsoid
passes the origin of the Cartesian coordinate system at the time
, moving at a constant velocity along the axis 
, the scalar and vector potentials of the field
at the point with the radius vector 
outside of
the ellipsoid will equal:
, 
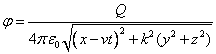, (7)
where 
is the
vacuum permittivity.
The electric
field strength 
and the
magnetic induction 
of the
Heaviside ellipsoid at the point with the radius vector are
calculated as follows:
,
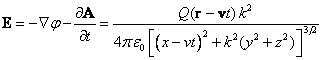. (8)
In Eq. (8) it is assumed that the velocity of the
ellipsoid’s motion is directed along the
axis and has
the components 
, 
.
Based on the
results obtained by Heaviside [4] and Searle [6], we will write the expression
for the electromagnetic energy outside the charged Heaviside ellipsoid [6, page
340, eq. (24)]:
, (9)
where
, 
is
the field energy around a stationary charged sphere; at 
the
Heaviside ellipsoid turns into this sphere.
We will
assume that Eq. (4), connecting the mass and
the energy of the particle, is also valid for the electromagnetic field. In
this case, the effective mass of the electromagnetic field associated with the
external field energy will be:
. (10)
The momentum
of the electromagnetic field outside the charged Heaviside ellipsoid was
calculated in [7]:
. (11)
From Eq. (11) similarly to Eq.
(5) we obtain the effective electromagnetic mass associated with the momentum
of the external electromagnetic field:
.
(12)
Comparing
Eqs. (10) and
(12) we obtain:
. (13)
2.2. Internal Electromagnetic Field
It is well
known that the electromagnetic energy within the charged Heaviside ellipsoid is
equal to one-fifth of the external energy [8]. Using
Eq. (9), for the electromagnetic energy and the effective mass of the
field inside the Heaviside ellipsoid we have the following:
,
(14)
, (15)
where 
is the field energy inside the fixed uniformly charged ball.
Similarly to Eq. (14) for energy, the momentum of the
electromagnetic field inside the charged Heaviside ellipsoid is five times less
than in Eq. (11):
.
(16)
From Eq. (16) we obtain the effective mass of the field
associated with the momentum of the electromagnetic field inside the charged
ellipsoid:
.
(17)
From
Eqs. (15) and
(17) we obtain the relation for the masses of the field inside the ellipsoid,
similar to the relation for the masses of the field outside the ellipsoid in Eq. (13)
. (18)
The
difference between the masses 
and 
in Eq. (13), and the masses 
and 
in Eq. (18) is the essence of the so-called 4/3
problem, according to which the field masses and , calculated through the field momentum at low
velocities are approximately 4/3 more than the corresponding field masses and , found through the field energy.
3. ENERGY – MOMENTUM OF THE EXTERNAL
AND INTERNAL GRAVITATIONAL FIELD OF THE HEAVISIDE ELLIPSOID
The
characteristic feature of the fundamental fields, which include the gravitational
and electromagnetic fields, is the similarity of their equations for the
potentials and the field strengths. This follows from the equations of
gravitomagnetism, which are the consequence of the general theory of relativity
in consideration of phenomena in a weak field. In the Lorentz-invariant theory
of gravitation [3, 9, 10] the similarity of equations for both fields is even
more apparent. Accordingly, 4/3 problem also takes place for the gravitational
field. We considered this issue previously with respect to the gravitational
field of a moving ball [11-13]. We will present here the obtained results in
order to compare them with the formulas for the effective masses of the
electromagnetic field and then to include the masses of the gravitational and
electromagnetic fields in the total mass of the system which consists of the
body and its fields.
According to
the Lorentz-invariant theory of gravitation (LITG), when a ball with the radius
is moving at the velocity in empty
space, the surface of the ball must be replaced with the Heaviside ellipsoid.
The ball becomes somewhat compressed along the velocity of motion, one axis
becomes shorter and is assumed to be 
. We will remind that in LITG in all the formulas
the gravitation propagation speed 
is used
instead of the speed of light 
. In LITG not only the theory of gravitation, but
also the theory of relativity as part of LITG is constructed so that the speed
of light everywhere is replaced by . Thus it is assumed that space-time measurements
can be carried out by means of gravitational waves in the same way as it is
done by means of electromagnetic waves.
In
gravitomagnetism, which follows from the general theory of relativity, in the
weak field limit it is assumed that the speed of gravitation is equal to the
speed of light. This leads to the fact that for the Heaviside ellipsoid one
axis along the velocity of motion is 
, as in the case of the electromagnetic field,
discussed in Section 2.
3.1.
External Gravitational Field
We will
assume that the ball with the gravitational mass 
is moving along the axis 
of some
reference frame. As in the case of the electromagnetic field, we can introduce
for the gravitational field in LITG the scalar and vector potentials 
at an
arbitrary point in space 
, which for the ball are as follows:
, 
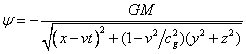, (19)
where 
–
the gravitational constant.
In Eq. (19) it is assumed that at 
the center
of the ball (the center of the Heaviside ellipsoid) is located in the origin of
the coordinate system. We can notice that the gravitational potentials in Eq. (19) are similar by their form to the potentials
in Eq. (7) of the electromagnetic field.
Further we
will consider that 
, then the subsequent results will have the same
form both in LITG and in gravitomagnetism. With the help of field potentials in
Eq. (19) it is easy to determine the
gravitational field strength and the torsion field (gravitomagnetic field),
which are the analogues of the electric field strength and the magnetic
induction, respectively. The energy of the gravitational field outside the
moving ball is written similarly to Eq. (9):
,
(20)
where 
is the field energy around the stationary
ball.
The effective
mass of the field, associated with energy, is found similarly to Eq. (10):
. (21)
The momentum
of the gravitational field outside the Heaviside ellipsoid equals:
, (22)
from
this the effective mass of the field associated with the momentum is as
follows:
. (23)
Comparing Eqs. (21) and (23) gives:
.
(24)
The
difference between the masses of the gravitational field in Eq. (24) is the same as for the masses of the
electromagnetic field in Eq. (13). This means
that the 4/3 problem takes place in case of the gravitational field.
3.2. Internal Gravitational Field
The
potentials of the gravitational field inside the uniform ball, which takes the
form of the Heaviside ellipsoid due to the motion, were calculated in [12, 13]
by adding the retarded potentials of all the point masses that made up the
ball. As a result the gravitational energy inside this Heaviside ellipsoid
equals:
,
(25)
where 
is the field energy inside a stationary ball
with radius .
The
effective mass of the field associated with energy is obtained similarly Eq. (4):
.
(26)
For the
momentum and the effective mass of the gravitational field inside the Heaviside
ellipsoid we find:
, (27)
. (28)
From
Eqs. (26) and (28) the relation follows for the effective masses of
the field, which is similar to Eq. (24) and
leads to the 4/3 problem:
.
(29)
4.
THE CONTRIBUTION OF GRAVITATIONAL FIELD IN ENERGY AND MOMENTUM OF A MOVING BODY
We
shall try to include in equation (1) the relations found above for the energy
and the momentum of the gravitational field of a moving body in the form of a
ball. We shall suppose as a first approximation that in static case instead of Eq. (3) there is the following relation
for the relativistic energy of system:
,
(30)
where 
–
the integral energy of static gravitational field inside and outside the ball
with uniform density,
– the gravitational mass
of the ball,
– the rest energy, found in such a way that it does not depend
on the energy of the macroscopic gravitational field. To determine the energy 
the ball’s
substance should be divided into pieces and spread to infinity while the
total mass of all pieces of the body is 
.
The choice of
the minus sign in front of 
in Eq. (30) will be
substantiated in Section 5, where the relativistic energy of the system is
reduced to the binding energy of the system, and all the energy components are
included in the energy expression in Eq. (45)
with negative signs. In Eq. (30) all terms must be
associated with the relativistic energy either of the system, or of the body,
or of the body field. We believe that the field energy 
is a component of the total, not the
relativistic energy. Due to the relation between the total energy and the
binding energy, which are equal in the absolute value but differ in signs, we
take with the minus sign.
Similarly
to Eqs. (1) and (4) we define the
relativistic energy of the moving system:
. (31)
On
the other hand, the gravitomagnetic energy as the integral energy of the gravitational field inside and outside the
ball, taking into account Eqs. (20) and (25) is
negative and equals:
.
For
the relativistic energy of the system in the form of the moving ball and its
field, we have as in Eq. (30):
. (32)
From Eqs. (31)
and (32) it follows:
. (33)
Since
the energy of the static field is negative: 
, then in Eq. (33) in the energy 
of the moving ball the negative additive from
field energy will appear, and the energy does not
depend on 
.
We
shall consider now the law of conservation of momentum. The momentum of the
system consists of the momentum of the ball 
and the momentum of the gravitational field, and taking into account Eq.
(22) for the field momentum outside the ball, and Eq. (27) for the momentum of
the field inside the ball, the total momentum of the field is:
.
Then
for the momentum of the system we can write down:
, (34)
where 
is the mass of moving ball as a function of
the velocity 
.
Momentum of the system
can also be expressed as in Eq. (4), taking into account Eq. (30) we find:
. (35)
From comparing Eqs. (34) and (35) it follows:
. (36)
From
Eq. (33) it follows that at 
the rest energy of the pieces of ball
at infinity does not include the field energy, but with the addition of pieces
in the ball and subsequent movement of the ball in the energy an additive appears, related with the energy of the field. The field energy also makes contribution to the mass of the moving ball in Eq. (36).
Comparing Eqs.
(31) and (35) with Eq. (1) shows that taking into account the gravitational
field the role of the total mass of the body and its field is played by the
quantity 
. If we know the energy in Eq. (31)
and the momentum 
in Eq. (35), it follows from these relations that we can express the
mass 
of the system and the velocity of the body. In case of a uniform ball with
radius we can write down:
, 
.
(37)
According to Eq. (37), the invariant system mass depends not only on the energy and momentum
of the body, but also depends on the average body size due to the contribution
of the gravitational field mass to the constant value of the mass
.
We shall note
also that the problem of 4/3 for the gravitational field (inequality of the
mass of the field, found from the energy, and the mass of the field, calculated
by the momentum of the field) was compensated by the dependence of the energy in Eq. (33) and the mass in Eq. (36)
of the moving ball on the field energy . As a result, the field energy in Eqs. (31) and (35) is included symmetrically in both the relativistic energy and momentum
of the system. In this case,
our task was not to solve the 4/3 problem as such, but to take into account the
energy and momentum components of the gravitational field associated with the
system.
5.
ANALYSIS OF THE COMPONENTS OF MASS AND ENERGY OF THE SYSTEM
5.1.
Gravitational Field
Until now we
have not specified of which components the mass of the system consists, and
whether other energies except the energy of gravitational field contribute to
it. For example, what shall happen if the body is heated? From the standpoint
of kinetic theory, an increase of temperature leads first to an increase of the
average velocity of the particles that makeup the body. In this case, according
to Eq. (1) the
average energy of each particle of the body would increase, and due to the
additivity of energy the energy 
of the system should change. For the case of
the body at rest and its gravitational field 
, and for Eqs. (31) and (35) for
moving body we can write down the following:
, 
.
(38)
Heating of
the body from an external source leads to the change of in Eq. (38), and the heat as a form of energy
is distributed between the kinetic energy of substance and the energy of the gravitational field. When heated, the mass density could decrease
and the body radius could increase.
Any interaction between particles of the
body with each other or with the environment, which changes the energy of the particles, also changes the energy 
of the system at rest. In accordance with Eq. (37) the mass of the system with the ball depends not only on , but also on the radius of the ball .
5.2.
Electromagnetic Field and Internal Kinetic Energy
Suppose that some charge 
is uniformly distributed within a stationary
ball. In this case, taking into account Eqs. (9) and (14) the total energy of the electric field is:
.
(39)
The electromagnetic energy
may include the energy of the magnetic field 
, if the
ball is magnetized or if there are electric currents. The energies 
and together constitute the total energy 
of the electromagnetic field of the body,
which should contribute to the energy of the system.
We assume that other
forms of energy (e.g. heat) can change the body mass, but can
not change the charge of the body, because it is necessary to transfer
the charged particles to the body (or from the body). This is one of the
differences between the electromagnetic and gravitational fields, in addition
to the unipolarity of gravitational charges (which are the masses) and the
bipolarity of electromagnetic charges.
The mass in Eq. (30) is the total mass of all body parts,
separated to infinity. As in [14] we can assume that in this case the substance
is at zero degrees according to Kelvin temperature scale. When integrating all
parts into a single body the substance temperature increases up to the value 
and a certain mass 
appears,
which presents the additional mass of the internal kinetic energy 
of the body. This energy includes the kinetic
energy of motion of atoms and molecules, the energy of turbulent motion of the
substance fluxes, as well as the energy of oscillations and rotations of atoms
and molecules and the energy of their additional interaction as a result of
substance heating.
If 
is the average velocity of particles in the
body at temperature , then the following approximate
relations would hold: 
, 
.
Since we intend to include
the electromagnetic energy of the ball and the kinetic energy of the
set of atoms and molecules of the ball’s substance to the total energy of the
system, we introduce new notation: will be replaced by 
, will be replaced by 
, 
will be replaced by 
. Similarly to Eq.
(30) we can then write:
.
(40)
As the energy of field, we include the
energy 
in Eq. (40) with the negative sign.
For the body that is only under influence
of its proper gravitational and electromagnetic field, the virial theorem is
satisfied, according to which the absolute value of potential energy of the
field on the average is twice as much than the kinetic energy of body particles:
, 
, (41)
here 
is the total energy excluding the rest energy
of the particles of the body.
Substituting Eq. (41) in Eq. (40)
gives the approximate equality:
. (42)
6. MASS OF THE BODY AT 00 KELVIN
We shall now consider the essence of the
mass 
related to the total mass of body particles
excluding the contribution from the mass of the internal kinetic (thermal)
energy and the energy of macroscopic fields. The contributions in mass are made by the masses of various types of
energy associated with atoms and molecules at the temperature near absolute
zero: strong interaction, binding the substance of the elementary particles and
retaining the nucleons in atomic nuclei; electromagnetic interaction of
particles; the energy of motion of electrons in atoms; rotational energy of
atoms and molecules; vibrational energy of atoms in molecules, energy of atoms
in molecules, etc.
6.1. Strong Interaction
In Standard Model it is assumed that the
strong interaction arises due to the action of the gluon field between the
quarks located in the hadrons (mesons and baryons), and the strong interaction
between leptons is absent.
There is also a hypothesis that the strong
interaction is a manifestation of strong gravitation at the level of elementary
particles and atoms [15]. According to the Lorentz-invariant theory of
gravitation, there are two components, in the form of gravitational field
strength and the torsion field, and the stability of nucleons in nuclei can be
described as the balance of forces from the attraction of the nucleons to each
other due to strong gravitation, and the repulsion of nucleons due to the
torsion field [3]. The same idea is applied to describe the structure and the
stability of a number of hadrons, considered as the composition of nucleons and
mesons [12]. Strong gravitation differs from the ordinary gravitation by replacing
of the gravitational constant 
by the constant of strong gravitation
, and acts between all particles,
including leptons. The estimation of the quantity can be obtained from the balance of four
forces acting on the electron in the hydrogen atom: 1. The
force of electric attraction between the electron and the atomic nucleus. 2.
The force of electric repulsion of the charged matter of the electron from
itself (the electron is represented as a cloud around the nucleus). 3. The
centripetal force from the rotation of the electron around the nucleus. 4. The
attraction of the electron to the nucleus under the influence of strong
gravitation. These forces are approximately equal to each other, so the
relations for the forces of attraction from strong gravitation and the electric
force are satisfied [9]:
, 
m3∙kg –1∙c –2 , (43)
where 
and 
– the mass of proton and electron,
respectively,
– the radius of
rotation of the electron cloud,
– the elementary
electric charge as the proton charge equal to the absolute value of the
negative charge of electron,
– the vacuum
permittivity.
Another way to estimate is based on the theory of similarity of matter
levels and the use of coefficients of similarity. These coefficients are
defined as follows: 
– coefficient of similarity by mass (the ratio
of the mass of neutron star to the proton mass); 
– the coefficient of similarity by size (the
ratio of the radius of neutron star to the proton radius); 
– the coefficient of similarity by speed (the
ratio of the characteristic speed of the particles of neutron star to the speed
of light as the typical speed of the proton matter). For strong gravitational
constant a formula is obtained: 
, where exponents of similarity
coefficients correspond to the dimension of gravitational constant according to the dimensional analysis.
If we understand the strong interaction as
the result of strong gravitation, the main contribution to the proton rest
energy should be made by the positive kinetic energy of its matter and the
negative energy of the strong gravitation (the electrical energy of the proton
can be neglected due to its smallness). The sum of these energies gives the
total energy of the proton, and due to the virial theorem in Eq. (41) this sum of energies is approximately
equal to half of the energy of strong gravitation. Since the energy of the strong
gravitation is negative, then the total energy of the proton is negative too.
The total energy of the proton up to the sign can be regarded as the binding
energy of its matter; the binding energy equals to the work that should be done
to spread the matter to infinity so that there total energy of the matter
(potential and kinetic) should be equal to zero. According to its meaning, the
positive proton rest energy must be equal to the binding energy or the absolute
value of the total energy of the proton. This gives the equality between the
rest energy and the absolute value of half of the energy of strong gravitation:
,
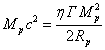(44)
where 
for the case if the proton was uniform density
ball with the radius
.
If we substitute Eq. (43) in Eq. (44), we obtain another equation, which allows estimating the radius of the
proton:
, 
,
where 
is the classical
electron radius.
In self-consistent model of the proton
[16] we find that in Eq. (44) the radius of the proton is 
m, and the coefficient 
due to a small increase in the density in the
center of the proton. At the same time, in the assumption that positive charge
is distributed over the volume of proton similar to the mass distribution and
the maximum angular frequency of the proton rotation is limited by the
condition of its integrity in the field of strong gravitation, we can find the
magnetic moment of the proton as a result of rotation of its charged matter:
,
where 
J/T is the magnetic moment of the proton,
(in the case of the uniform density and the charge of proton
it should be 
).
The fact that the rest energy of the
proton is associated with strong gravitation, also
follows from the modernized Fatio-Le Sage theory of
gravitation [17]. In this theory, based on the absorption of the fluxes of
gravitons in the matter of bodies with transfer of the momentum of gravitons to
the matter, the exact formula for Newton's gravitational force (the law of
inverse squares) is derived; the energy density of the flux of gravitons (
J/m3), the cross section of their
interaction with the substance (
m2) and other parameters are
deduced.
In the theory of infinite hierarchical nesting of
matter [3], [9] it is shown that at each main level of matter the corresponding
type of gravitation appears: there is a strong gravitation at the level of
elementary particles, but at the level of stars it is the ordinary gravitation.
The gravitation reaches a maximum in the densest objects – in nucleons and in neutron stars. In the substance
of the earth's density the range of strong gravitation is less than a meter,
and at such sizes of bodies strong gravitation is replaced by the ordinary
gravitation. This corresponds to the fact that the masses and the sizes of
objects at different levels of matter increase exponentially, and the point of
replacing of the strong gravitation by the ordinary gravitation lies near the
middle of the range of masses from nucleons to the stars on the axis of the
masses on the logarithmic scale.
In the above picture the rest energy of
proton in Eq. (44)
is approximately equal to the absolute value of the total energy of the proton
in its proper field of strong gravitation (for increased accuracy we should
also take into account the electromagnetic energy of the proton), and the
energy 
in Eq. (42) consists of the rest energy of nucleons and electrons of the matter of
the body, with the addition of the energy of their gravitational and
electromagnetic interactions and the mechanical motion in atoms and molecules.
Consequently, the energy of the body, taking into account the virial theorem
in Eq. (41)
can be reduced to the half of the absolute value of the sum of the energy of
strong gravitation 
and electromagnetic energy 
of the nucleons, electrons, atoms and
molecules involved in formation of the binding energy. As a result, the relativistic
energy of the stationary body and its fields instead of Eq. (42) can be written down as follows:
.
(45)
To understand
the meaning of energy better, we shall consider the energy balance
in the process of merging of matter, with formation of elementary particles at
the beginning, passing then to confluence of the elementary particles into
atoms and finally in the formation of a body of many atoms. Initially, the
matter is motionless at infinity and its parts do not interact with each other,
so that total energy of the system is zero (we do not consider here the rest
energy of matter in its condition when it is fragmented and was not yet
included into the composition of the elementary particles). If the matter
particles will draw together under the influence of strong then ordinary
gravitation, the negative energy of gravitational field and the positive
kinetic energy of motion of particles will appear, and due to
the energy conservation law the integral energy should not change, remaining
equal to zero. In the energy balance it is necessary to take into account the
electromagnetic energy 
and the energy 
leaving the system due to the emission of
field quanta such as photons and neutrinos:
, 
. (46)
In Eq. (46) the virial theorem in the form of Eq. (41)
is used for the components of the total energy 
of the system. According to Eq. (46), the energy of the emission that left the system equal up
to a sign to the total energy , i.e. the
energy of emission equals the binding energy of the system. By comparing Eqs.
(46) and (45) we now see
that the relativistic energy of body and its field is the same as the
energy extracted from the body by different emission during the formation of
the body.
As a rule in the
energy only those components are taken into account
that are associated with formation of elementary particles, atoms and
macroscopic molecular substance; and the binding energies of the particles of
which the matter of elementary particles is built are not taken into account
and are assumed to be constant. Heating the body due to
gravitation according to Eqs.
(46) and (45) leads to an increase of body energy . This
conclusion is based on the fact that although the internal kinetic energy of
the body is part of Eq. (40)
with the negative sign, but the change of the potential energy 
by the virial theorem compensates the
contribution of the energy. An
example is the star, which is heated and accelerates its rotation during
compression by gravitation, and the absolute value of the gravitational energy
of the star increases.
According to Eq. (45), the relativistic energy of the system consists mainly of the energies
of two fundamental fields – gravitational and electromagnetic, responsible for
the integrity of the particles of the body and for the composition of the body
of the individual particles. In this case, the strong interaction between the
particles is taken into account by the energy of strong gravitation and the electromagnetic energy
.
6.2. Weak Interaction
As for the weak interaction it is assumed
to be the result of transformation of matter, which was for a long time under the
influence of the fundamental fields. An example is the long-term evolution of a
star massive enough to form a neutron star in a supernova outburst, when the
neutrino burst is emitted with the energy of about the binding energy of the
star (the gravitational energy of the matter compression into a small-sized
neutron star is converted into the energy of neutrinos, the energy of photon
emission, the kinetic energy and the heating of the expelled shell). At the
level of elementary particles, this corresponds to the process of formation of
a neutron with the emission of neutrino.
If in the weak interaction the body at
rest emits (the body absorbs) neutrinos, photons and other particles, it leads
to a change of the relativistic
energy of the system. In
general, the energy is the function of time
and speed with which the separate particles or units of matter are emitted from
the body or absorbed by it. Due to the laws of conservation of energy and
momentum, if some particles bring into the system the energy and momentum, then
after some time they are distributed in the system and according to virial
theorem they can be taken into account through the energy and the momentum of
the fundamental fields. Therefore, we
can state that according to Eq. (45), the source of the energy of the system, and of its mass 
as the measure of inertia are the
gravitational and electromagnetic fields associated with the masses and
charges, as well as electric currents and mass flows. In Fatio-Le
Sage theory of gravitation it is supposed
that the fields are the consequence of the interaction of the masses and the
charges with the fluxes of gravitons and tiny charged particles that penetrate
the space.
If we define the
total mass of the system in the form 
, then Eq. (38) for energy and momentum of a moving body is as follows:
,
. (47)
7. CONCLUSIONS
Equations (47) look exactly the same as Eq. (1) for a small test particle. However, the
mass 
of system in Eq. (47)
takes fully into account the field energies, whereas for the mass 
of a small particle in Eq. (1) it is only expected. The
appearance in the mass of the contribution from the energy of fields
has occurred because we have used the energy of mutual interaction of many
small particles in a massive body. Hence, by induction, we should suppose that
not only the mass of body, but the mass of any isolated small particle should
be determined taking into account the contribution from the energy of proper
fundamental fields of the particle. The described concept of mass in the covariant theory of
gravitation (CTG) is confirmed by the analysis of the Hamiltonian [18] and of
the Lagrangian in the principle of least action [19].
We
should note the difference between the results of CTG and general theory of
relativity (GTR) with respect to mass and energy. In CTG the mass of system
with the uniform spherical body at rest with the radius 
including effective mass of its fields is expressed with the help of Eqs. (39) and (45):
, (48)
where the mass sets the total mass of body parts at zero
absolute temperature, excluding the potential energy of the fields, the mass 
is obtained through the density and the volume
and represents the gravitational mass, the expression for the energy is given after Eq. (30).
As
a result the relativistic mass of the system by combining the body parts into
a whole increases due to the energy of the gravitation field , and decreases due to the electric
energy 
.
In general theory of
relativity in order to determine the mass of a stationary system we can
integrate the timelike component of the stress-energy tensor of the system 
over the volume and divide the result by the
squared speed of light. According to [20] for the gravitational field
contribution and [21] with respect to the electromagnetic field, the mass of
the system in the first approximation is:
,
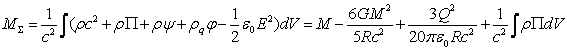(49)
where 
is the body mass, 
and 
are the density of mass and charge,
respectively, 
and 
define the scalar potentials of the
gravitational and electric field, respectively, 
is the vacuum permittivity, is the electric field intensity, 
is the elastic energy per unit mass. In this
case the mass density is associated with the scalar potential by the
Poisson equation 
and satisfies the continuity relation of the
special theory of relativity.
Since the potential is negative and the potential is positive, in Eq. (49) the substance energy in the
gravitational field reduces the mass , while the
energy of the charges in the electric field and the elastic energy increase the system mass .
In GTR the gravitational
field potentials are described by the metric tensor components, and the field
and metric always exist in the presence of masses,
therefore instead of the invariant mass density 
is used. The invariant density is part of the
continuity relation in the curved spacetime: 
, here 
is the determinant of the metric tensor, 
is the 4-velocity. In a weak field for a fixed
body we can approximately write the following:
.
If based on this we express and substitute it in (49), we will obtain for
the mass-energy of the system an expression similar to those presented in [22]
and [23] (in contrast to [20], in [23] is the invariant density and 
denotes the mass density in special theory of
relativity).
In Eq. (49) not the mass but the mass 
is used, which is expressed through the mass
density and volume and included in the formula for the gravitational
energy. As it was shown in [18], for three masses associated with the system,
the following relation holds: 
, which also follows from Eqs. (48) and (49). In our opinion, the reason of difference between Eqs.
(48) and (49) is associated with different positions
of the two theories: in CTG there is explicit stress-energy tensor of
gravitational field, included in the Lagrangian and contributing to the
spacetime metric and the energy-momentum of the considered system. This allows
us to define all the three masses 
and to find their meaning, and the mass is associated with the cosmological constant
in the equation for the metric of the system. In GTR the principle of
equivalence is used instead of this, the gravitational field is reduced to the
metric field, and correspondingly, the energy and the momentum do not form
tensor and can be found only indirectly, through the spacetime metric.
Eqs.
(48) and
(49) imply consistency of
positions CTG and GTR, as these theories determine the mass and energy from
different standpoints.
REFERENCES
1. C. W. Misner, K. S. Thorne,
and J. A. Wheeler, Gravitation (W. H.
Freeman, San Francisco, CA, 1973).
2. L. B. Okun, Nucl. Phys. B (Proc.
Suppl.). 110, 151 (2002).
3. S. G. Fedosin, Fizicheskie teorii i beskonechnaia vlozhennost’ materii (Perm, 2009).
4. O. Heaviside, The
Electrician. 22, 147 (1888).
5. O. Heaviside, Philos. Mag. Series 5. 27, 324 (1889).
6. G. F. C. Searle, Philos. Mag. Series 5. 44, 329 (1897).
7. S. Hajra, J. Mod. Phys. 3, 187 (2012).
8. S. Hajra, Ind. J. Theor. Phys. 42,
164 (1991).
9. S. G. Fedosin, Fizika i filosofiia podobiia: ot preonov
do metagalaktik (Perm, 1999).
10.
S.
G. Fedosin, Apeiron. 14, 385
(2007).
11.
S.
G. Fedosin, Journal of Vectorial Relativity. 3, 30 (2008).
12.
Comments to
the book: S. G. Fedosin, Fizicheskie teorii i beskonechnaia vlozhennost’ materii (Perm, 2009).
13.
S.
G. Fedosin, Advances
in Physics Theories and Applications. 23, 19 (2013).
14.
S.
G. Fedosin, Caspian Journal of Applied Sciences
Research. 1, 1 (2012).
15.
C.
Sivaram and K. P. Sinha,
Phys. Rev. D. 16, 1975 (1977).
16.
S.
G. Fedosin, Hadronic Journal. 35, 349 (2012).
17.
S.
G. Fedosin, Journal of Vectorial Relativity. 4, 1 (2009).
18.
S.
G. Fedosin, Advances
in Natural Science. 5, 55 (2012).
19.
S.
G. Fedosin, Hadronic Journal. 35, 35 (2012).
20.
V.
A. Fock, The Theory of
Space, Time and Gravitation (Pergamon
Press, London, 1959).
21.
L.D.
Landau and E.M. Lifshitz, The Classical Theory of Fields (Vol. 2,
4th ed. Butterworth-Heinemann, 1975).
22.
A. Papapetrou, Proc. Phys.
Soc. A. 64, 57
(1951).
23.
S. Chandrasekhar,
Ap. J. 142, 1488
(1965); Ap. J. 158, 45
(1969).
Source: http://sergf.ru/emen.htm