Progress In Electromagnetics Research C, Vol. 96, pp. 109-122 (2019). https://doi.org/10.2528/PIERC19062902
О
ковариантном представлении интегральных уравнений электромагнитного поля
Федосин Сергей Григорьевич
ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
В ковариантном виде представляются интегральные теоремы Гаусса для электрического и магнитного полей, закон электромагнитной индукции Фарадея, теорема о циркуляции магнитного поля, теоремы о потоке и циркуляции векторного потенциала, действительные в искривлённом пространстве-времени. Даются ковариантные формулы для магнитного и электрического потоков, для электродвижущей силы и для циркуляции векторного потенциала. В частности, электродвижущая сила выражается криволинейным интегралом второго рода по замкнутому контуру, при этом в интеграле кроме напряжённости вихревого электрического поля появляется ещё определитель метрического тензора. Подобно этому, магнитный поток выражается поверхностным интегралом второго рода от произведения индукции магнитного поля на определитель метрического тензора. Вводится новая физическая величина – интегральный скалярный потенциал, скорость изменения которого со временем задаёт поток векторного потенциала через замкнутую поверхность. Показывается, что обычно применяемая четырёхмерная теорема Кельвина-Стокса не позволяет в полной мере вывести интегральные законы электромагнитного поля и в ковариантной записи требует добавки определителя метрического тензора, при этом ещё действие теоремы Кельвина-Стокса ограничено случаями, когда определитель метрического тензора и площадь контура не зависят от времени. Этого недостатка лишён подход с использованием теоремы о дивергенции и уравнения для дуального тензора электромагнитного поля. Проблема интерпретации закона электромагнитной индукции и теоремы о циркуляции магнитного поля не может быть решена на основе силы Лоренца в отсутствие зарядов и потому требует более общего подхода, когда учитывается преобразование компонент полей из покоящейся в движущуюся систему отсчёта. Предсказывается новый эффект, согласно которому циркуляция магнитного поля может появиться даже в отсутствие электрического тока и при постоянном электрическом поле сквозь контур, если будет изменяться площадь этого контура. По аналогии с электромагнитной индукцией, для возникновения циркуляции магнитного поля оказывается важным изменение во времени потока электрического поля через площадь контура.
Ключевые
слова:
теорема Гаусса;
закон электромагнитной индукции; теорема о циркуляции; теорема
Кельвина-Стокса; теорема о дивергенции; магнитный поток; электрический
поток; электродвижущая сила; векторный потенциал; дуальный тензор.
On the covariant representation of integral
equations of the electromagnetic field
Sergey G. Fedosin
PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia
E-mail: fedosin@hotmail.com
Gauss integral
theorems for electric and magnetic fields, Faraday’s law of electromagnetic
induction, magnetic field circulation theorem, theorems on the flux and
circulation of vector potential, which are valid in curved spacetime, are
presented in a covariant form. Covariant formulas for magnetic and electric
fluxes, for electromotive force and circulation of the vector potential are
provided. In particular, the electromotive force is expressed by a line
integral over a closed curve, while in the integral, in addition to the vortex
electric field strength, a determinant of the metric tensor also appears. Similarly, the
magnetic flux is expressed by a surface integral from the product of magnetic
field induction by the determinant of the metric tensor. A new physical
quantity is introduced – the integral scalar potential, the rate of change of
which over time determines the flux of vector potential through a closed
surface. It is shown that the
commonly used four-dimensional Kelvin-Stokes theorem does not allow
one to deduce fully the integral laws of the electromagnetic field and in the covariant notation requires the addition
of determinant of the metric tensor, besides the validity of the
Kelvin-Stokes theorem is limited to the cases when determinant of metric tensor
and the contour area
are independent from time. This disadvantage is not present
in the approach that uses the divergence theorem and equation for the dual
electromagnetic field tensor. The problem of interpreting the law of
electromagnetic induction and magnetic field circulation theorem cannot be
solved on the basis of the Lorentz force in the absence of charges, and
therefore requires a more general approach, when transformation of the field
components from the reference frame at rest into the moving reference frame is
taken into account. A new effect is predicted, according to which the circulation of
magnetic field can appear even in the absence of electric current and with a
constant electric field through the contour, if the area of this contour would change. By analogy
with electromagnetic induction, for the magnetic field circulation to appear it
is important that electric field flux that passes through the area of the contour would change
over time.
Keywords: Gauss integral theorem; electromagnetic induction; circulation theorem; Kelvin-Stokes theorem; divergence theorem; magnetic flux; electric flux; electromotive force;
vector potential; dual electromagnetic tensor.
В классической электродинамике уравнения
электромагнитного поля записываются в виде уравнений Максвелла:
,
(1)
,
(2)
,
(3)
,
(4)
где 
и 
представляют собой трёхмерные
векторы напряжённости электрического поля и индукции магнитного поля,
соответственно; 
есть плотность заряда движущегося элемента вещества с точки зрения
неподвижного наблюдателя; 
обозначает плотность
электрического тока; 
– электрическая
постоянная; 
– магнитная
постоянная; 
– скорость света,
причём 
.
Теорема о дивергенции (Divergence
theorem) связывает
интеграл от дивергенции вектора по произвольному трёхмерному объёму 
с потоком данного
вектора через полную поверхность 
данного объёма. В
частности, для электрического поля можно записать:
,
(5)
где 
есть единичный вектор
нормали к поверхности , направленный наружу, и в декартовых координатах выражение 
задаёт компоненты
вектора напряжённости электрического поля.
Если проинтегрировать (1) по некоторому
объёму, внутри которого помещается заряд 
, и применить (5), получится интегральное уравнение в виде
теоремы Гаусса:
.
(6)
В общем случае заряды движутся и потому 
в интеграле в (6) есть
элемент объёма движущегося элемента вещества. В силу Лоренцевского сокращения
изменяется как плотность заряда , так и 
, однако комбинация 
после интегрирования
приводит к инвариантной величине заряда , а значит и к
сохранению потока через поверхность,
окружающую данный объём.
Если в (5) заменить на и учесть (2), получается
теорема Гаусса для магнитного поля:
.
(7)
Интегральное уравнение (7) говорит о
принципиальном отсутствии в любом объёме магнитных зарядов, которые в случае их
существования могли бы создавать ненулевой поток магнитной индукции через
замкнутую поверхность .
При интегрировании уравнения (3) используется теорема Кельвина-Стокса, связывающая поток ротора
векторного поля через некоторую двумерную поверхность , и циркуляцию этого поля по одномерному контуру 
, ограничивающем данную поверхность. Для электрического поля
получается следующее:
. (8)
Из (3) и (8) следует закон электромагнитной
индукции Фарадея:
.
(9)
Как правило, поверхность и контур в теореме
Кельвина-Стокса считаются неподвижными, так что согласно (9) за счёт изменения
со временем магнитного поля 
, проходящего через поверхность, в контуре возникает вихревое
электрическое поле 
. Когда имеются заряды, которые могут двигаться под действием
такого поля , говорят об электродвижущей силе 
в выбранном контуре.
Если вместо подставить в (8) и результат
использовать для интегрирования (4) по поверхности, получается выражение
интегральной теоремы о циркуляции магнитного поля по контуру :
.
(10)
В (10) 
обозначает суммарную
перпендикулярную компоненту силы тока, проходящего через поверхность , 
задаёт скорость
изменения во времени электрического поля, пересекающего поверхность. Как 
, так и поток величины
генерируют вихревое
магнитное поле в контуре 
, ограничивающем поверхность .
Представленные выше стандартные формулы (1-10)
записаны для трёхмерных векторов. Мы привели их здесь с тем, чтобы затем
сравнить с формулами для четырёхмерных векторов и тензоров, справедливыми не
только в плоском пространстве-времени Минковского, но и в искривлённом
пространстве-времени. Как будет показано далее, получение четырёхмерных
интегральных уравнений электромагнитного поля позволяет не только обобщить
трёхмерные интегральные уравнения, но и получить более точное описание явлений.
В
частности, мы покажем, как может быть решена проблема интерпретации закона
электромагнитной индукции [1]. Действительно, согласно (9) электродвижущая сила 
в неподвижном контуре
возникает за счёт изменения со временем магнитного поля через площадь внутри
контура. Однако хорошо известно и подтверждено экспериментами, что изменение
площади контура при неизменном магнитном поле также создаёт электродвижущую
силу в контуре. Таким образом, в (9) производная по времени должна быть не
внутри, а перед интегралом по площади контура. Поскольку это не учитывается в
(9), обычно используется иное объяснение, с привлечением силы Лоренца [2]. В то
же время, преимуществом четырёхмерного описания оказывается возможность учесть
в одной формуле сразу обе стороны электромагнитной индукции, включающие в себя
изменения и магнитного поля, и площади контура.
Особенностью
представленного подхода является то, что основные следствия возникают после
применения теоремы о дивергенции к четырёхмерных уравнениям электромагнитного
поля, содержащим тензор электромагнитного поля 
и
дуальный ему тензор 
. При этом становится видно, что четырёхмерная
теорема Кельвина-Стокса может быть получена путём упрощения теоремы о
дивергенции и потому не требуется для вывода четырёхмерных интегральных
уравнений электромагнитного поля.
В
последнем разделе будет проанализирована интегральная теорема о циркуляции
магнитного поля и сделан вывод о том, что при увеличении площади контура в
постоянном электрическом поле в данном контуре должны возникать магнитное поле
и его циркуляция.
Дифференциальные
и интегральные уравнения электромагнитного поля в четырёхмерном искривлённом
пространстве-времени неоднократно рассматривались ранее. Если брать недавние
работы, то, например, в [3-5] все переменные величины и уравнения для них были
представлены путём расщепления компонент в 3+1 форме с точки зрения системы
отсчёта локального наблюдателя, рядом с которым движется рассматриваемый
элемент объёма с веществом и полем. В [6] рассматриваются квантовые уравнения
электромагнитного поля.
В
отличие от этого, нашей задачей является представление всех электромагнитных
величин и интегралов от них в ковариантной векторно-тензорной форме в
произвольной системе отсчёта для макроскопических систем, без предварительного
расщепления на отдельные компоненты векторов и тензоров.
2.
Ковариантные уравнения электромагнитного поля
В четырёхмерной формулировке учитывается то,
что компоненты электромагнитного тензора зависят только от компонент векторов 
и 
. Что касается плотности заряда 
и плотности электрического тока 
, то они входят в
4-ток 
, где 
есть плотность заряда
в сопутствующей элементу вещества системе отсчёта, 
есть 4-скорость
элемента вещества. В результате уравнения (1) и (4) заменяются одним
уравнением:
.
(11)
В свою очередь, уравнения (2) и (3) могут быть
получены из уравнения:
. (12)
Для этого в (12) необходимо использовать
несовпадающие друг с другом значения индексов 
. Другой способ подразумевает использование для
псевдоевклидового пространства-времени полностью антисимметричного символа
Леви-Чивиты 
, у которого по определению 
, где 
есть определитель
метрического тензора 
. Если задать дуальный тензор электромагнитного поля
выражением
,
(13)
умножить все члены (12) на 
и просуммировать,
получится 
. Таким образом можно считать, что уравнения (2) и (3) вытекают из уравнения:
где дуальный тензор согласно (13) имеет
следующие компоненты:
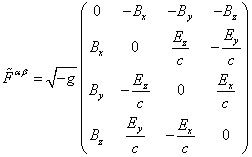. (15)
Два четырёхмерные уравнения (11) и (14) заменяют четыре трёхмерные уравнения Максвелла и являются стандартной записью уравнений электромагнитного поля в искривлённом пространстве-времени.
Так как тензор электромагнитного поля является антисимметричным тензором, его ковариантная производная может быть представлена через частную производную:
. (16)
Умножим обе части (16) на ковариантный
элемент 4-объёма 
, возьмём интеграл по объёму и используем теорему о
дивергенции в четырёхмерном виде:
, (17)
где 
есть ортонормированный
дифференциал 
трёхмерной
гиперповерхности, окружающей физическую систему в четырёхмерном пространстве, 
есть четырёхмерный
вектор нормали, перпендикулярный гиперповерхности и направленный наружу.
Умножим теперь правую часть (11) на 
и возьмём интеграл по
4-объёму:
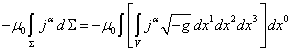. (18)
Из сравнения (11), (17) и (18) следует:
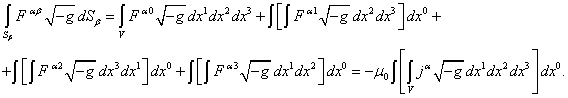
Продифференцируем
данное равенство по переменной 
, где 
– координатное время:
(19)
При 
первый член в (19)
обнуляется, так как 
. Для оставшихся членов с учётом равенства 
можно записать:
. (20)
Здесь 
есть ортонормированный элемент двумерной
поверхности, окружающей заряд 
; 
представляет собой поток электромагнитного
поля через замкнутую поверхность; трёхмерные индексы 
и не совпадают друг с
другом.
Было
также использовано соотношение из [7] для элемента объёма 
в сопутствующей
данному элементу системе отсчёта:
. (21)
Интегральное уравнение (20) является теоремой
Гаусса в ковариантной записи и обобщает уравнение (6).
Пусть теперь в (19) 
:
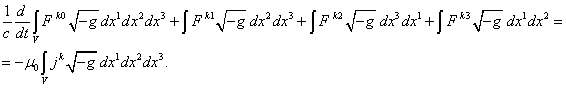
(22)
Рассмотрим (22) при 
. Так как по определению 
, то при 
, 
будет 
. Тогда в силу симметричности метрического тензора 
и антисимметричности
тензора электромагнитного поля 
получается, что в (22)
.
Предположим
теперь, что рассматриваемый объём таков, что его размер в направлении оси 
равен 
и мал по величине, так
что 
. Тогда результат интегрирования по дифференциалу 
в (22) можно
рассматривать как произведение подынтегральных выражений на 
. Так как 
, то в (22) можно будет сократить все члены на . Предварительно заменим элемент площади 
на 
, что меняет знак в соответствующем поверхностном интеграле
второго рода. Остаётся следующее:
Величину 
можно считать здесь
потоком электрического поля через поверхность в направлении оси 
, так как основной вклад в 
делает компонента 
, связанная с компонентой электрического поля 
. В общем случае каждая из компонент 
, 
и 
зависит сразу от всех
компонент тензора. Упростить ситуацию можно в рамках специальной теории
относительности, когда 
, причём компоненты метрического тензора 
пространства-времени
Минковского равны 0 либо 1 и не зависят
от времени и координат. В этом случае
будет 
, 
, 
, 
,
, и интегральное уравнение становится таким:
.
Это можно переписать подобно (10):
.
(23)
В (23) контур 
и поверхность 
находятся в плоскости 
, а циркуляция магнитного поля по этому контуру возникает за
счёт тока 
через площадь внутри контура, а
также в случае, когда имеется изменение со временем потока электрического поля
с напряжённостью 
, пересекающего площадь .
Интегральное уравнение (10) было получено с помощью теоремы Кельвина-Стокса, а уравнения (22) и (23) следуют из теоремы о дивергенции. Отсюда следует тесная связь между данными теоремами, поскольку видно, что для выполнения теоремы Кельвина-Стокса необходимо, чтобы толщина рассматриваемого объёма везде стремилась к нулю, независимо от ориентации частей этого объёма в пространстве. Существует однако различие между (23) и (10) в том, что в (23) берётся производная по времени от всего потока электрического поля по поверхности, а в (10) вместо этого присутствует только частная временная производная от электрического поля при неизменной площади поверхности. В результате интегральная теорема о циркуляции магнитного поля в виде (22) является более информативной, чем в (10), так как в (22) присутствуют интегралы по объёму и полная временная производная, а в (10) – лишь интегралы по поверхности.
3. Теорема Кельвина-Стокса в
четырёхмерном виде
Теорема
Кельвина-Стокса (8)
связывает интеграл от потока ротора трёхмерного вектора по некоторой площади с
циркуляцией этого вектора по контуру, ограничивающему указанную площадь. Четырёхмерное
обобщение теоремы
(8) можно найти,
например, в
[8]:
В интеграле по площади в (24) присутствует
4-ротор от 4-вектора 
:
.
Однако, как будет показано далее, (24)
справедливо лишь в рамках специальной теории относительности, а в искривлённом
пространстве-времени в (24) необходимо ввести определитель 
метрического тензора:
. (25)
Предполагается, что элемент площади в (25)
является антисимметрично ориентированным, так что выполняются соотношения:
, 
, 
, 
,
, 
, 
.
(26)
Рассмотрим случай, когда в (25) индексы 
, а 4-вектором является 4-потенциал
электромагнитного поля, рассматриваемый в некоторый момент времени. Тогда 
, где 
есть скалярный
потенциал, 
является векторным
потенциалом. При этом 
, и из (25) и (26) следует:
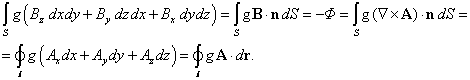(27)
В (27) было учтено, что 
. Согласно (27), поток магнитного поля 
через некоторую
фиксированную поверхность приводит к циркуляции
векторного потенциала 
по неподвижному
контуру, окружающему данную поверхность.
Возьмём частную производную по времени в (27) и переставим там члены:
. (28)
Индекс 
в (28) показывает, что
круговое электрическое поле 
и электродвижущая сила
в контуре 
возникают за счёт
изменения со временем магнитного поля, проходящего через контур, порождающего
изменение циркуляции векторного потенциала . Поскольку по определению электрическое поле возникает при
наличии градиента скалярного потенциала и изменении со временем векторного
потенциала, 
, то вихревое поле 
и электродвижущая сила
в (28) появляется в
отсутствие скалярного потенциала 
. Из сравнения (28) и (9) теперь видно, что закон
электромагнитной индукции можно представить как частный случай (25).
Запишем
(27) для практически замкнутой поверхности, когда контур 
становится настолько
мал, что его длина может считаться равной
нулю:
. (29)
Согласно (29), поток 
магнитного поля через замкнутую поверхность
равен нулю. В пределе специальной теории относительности 
и интегральное уравнение (29) переходит в
теорему Гаусса для магнитного поля в (7).
Рассмотрим теперь случай, когда в (25) с
учётом соотношения 
и (26-27) индексы пробегают все значения, 
:
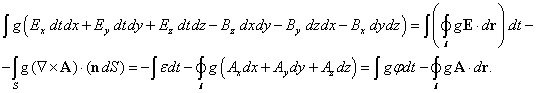
(30)
В (30)
была введена электродвижущая сила 
. Для выполнения интегрального уравнения (30) необходимо, чтобы было 
, то есть электродвижущая сила с точностью до множителя 
ведёт себя как
потенциал: 
. Отметим, что для совпадения электродвижущих сил 
и 
из (28) необходимо
выполнение соотношения 
, что возможно, если определитель 
не зависит от времени,
а вихревое поле 
в (30) порождается
лишь изменением во времени векторного потенциала .
4. Интегральные уравнения для
дуального тензора электромагнитного поля
Применим теорему о дивергенции к дуальному
тензору 
в (14), и действуя
аналогично (16) и (17), найдём:
. (31)
Распишем это интегральное уравнение по компонентам:
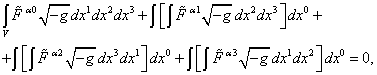
а затем возьмём производную
по переменной 
:
.
(32)
Уравнение
(32) при индексе 
с учётом компонент
дуального тензора в (15) можно записать так:
,
(33)
где есть определитель
метрического тензора 
.
Интегральное уравнение (33) как и (29)
представляет собой теорему Гаусса для магнитного поля и в пределе специальной
теории относительности переходит в (7).
Положим теперь в (32) индекс 
и используем (15):
. (34)
Предположим, что размер 
рассматриваемого объёма в направлении оси настолько мал, что
интегралы в (34) можно представить как произведения подынтегральных выражений
на 
. Тогда учитывая равенство 
, все члены в (34) можно сократить на и остаётся следующее:
.
Это можно переписать в векторном виде,
учитывая, что 
:
Для
рассмотренного выше случая , когда в (32) индекс и контур расположен в плоскости
, если контур обходится против часовой стрелки, то будет 
, а вектор 
направлен вдоль оси . При этом направление поля совпадёт с
направлением обхода контура против часовой стрелки, если поле 
будет увеличиваться со
временем и направлено против оси .
Интегральное уравнение (35) представляет собой
закон электромагнитной индукции Фарадея в ковариантной форме, где величина
есть магнитный поток
через поверхность 
, ограниченную проводящим контуром 
.
Обратим
внимание на то, что магнитный поток в (35) может меняться не только при
изменении со временем магнитного поля , но и при изменении площади поверхности 
. Таким образом, изменения как , так и могут вносить свой
вклад в циркуляцию электрического поля в контуре и в создание электродвижущей
силы 
. В отличие от этого, в интегральных уравнениях (9) и (28),
полученных из трёхмерной и четырёхмерной теорем Кельвина-Стокса соответственно, электродвижущая
сила возникает только за счёт изменения во времени векторного потенциала
магнитного поля в неподвижном контуре постоянной площади.
5. Анализ
интегральной теоремы о циркуляции электрического поля
В предыдущем
разделе было указано на ограниченность использования теоремы Кельвина-Стокса
для описания эффекта электромагнитной индукции. Полного описания данного
эффекта можно добиться путём применения теоремы о дивергенции к дуальному
тензору электромагнитного поля, приводящей к интегральному уравнению (35).
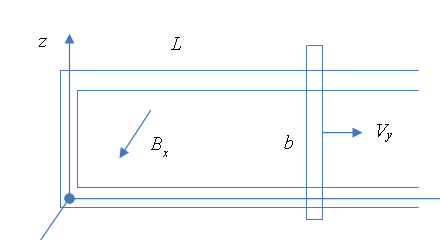
Применим (35) для описания стандартного опыта с рамкой, в которой имеется
движущаяся перекладина, позволяющая изменять площадь рамки. Конфигурация рамки
представлена на рисунке 1.
Пусть
высота перекладины равна 
, а текущее расстояние от начала координат до перекладины
равно 
, где 
есть скорость движения
перекладины вдоль оси 
. Постоянное магнитное поле 
направлено вдоль оси . В рамках специальной теории относительности определитель
метрического тензора и магнитный поток
вычисляется как интеграл от магнитного поля по площади рамки:
. (36)
Здесь мы предположили, что направление
обхода рамки на рисунке 1 происходит по часовой стрелке,
так что согласно правилу правого буравчика нормаль 
к
рамке направлена против оси и противоположно
вектору 
. При этом направление обхода должно совпадать с направлением
индукционного тока в перекладине.
Согласно (35) находим теперь электродвижущую силу как циркуляцию электрического поля на всей длине движущейся перекладины:
. (37)
В неподвижной
части рамки магнитное поле постоянно и там циркуляция электрического поля
должна быть равна нулю. Если учесть (30), то получается соотношение 
, то есть электродвижущая сила изменяется так же, как
электрический потенциал вдоль перекладины. В данном случае перекладина
становится генератором тока для всей рамки, источником энергии для которого
является сила, перемещающая перекладину в магнитном поле. Действительно, если
имеется проводящая цепь и генератор тока (например, электрическая батарея), то
внутри генератора при перемещении от катода к аноду потенциал увеличивается, а
затем падает вдоль цепи. Мы можем считать, что на рисунке 1 катод генератора индукционного
тока находится вверху, а анод – внизу перекладины.
Чтобы
подтвердить сказанное, необходимо представить, что происходит в перекладине при
её движении. Обычная интерпретация электромагнитной индукции при изменении
площади в магнитном потоке сводится к силе Лоренца, действующей в магнитном
поле на положительный заряд 
внутри перекладины:
,
. (38)
Далее
находится напряжённость электрического поля внутри перекладины, направленная против
оси 
, причём циркуляция поля совпадает с (37):
, 
, 
. (39)
Электродвижущая
сила 
положительна, так как
вектор 
в (39) направлен
внутри перекладины против оси , обходя рамку по часовой стрелки вслед за вектором 
. При этом направление обхода рамки совпадает с тем
направлением, которое было выбрано в (36) для определения направления нормали к рамке.
Рассмотренная
ситуация соответствует правилу Ленца, согласно которому возникающая за счёт
индукции электродвижущая сила порождает в проводящем контуре такой ток, что его
действие направлено противоположно тому действию, которое вызвало индукционный
ток. Эффект индукции в данном случае возникает от силы, перемещающей
перекладину с постоянной скоростью в магнитном поле, увеличивая площадь рамки.
Если вместо скорости 
подставить в (38)
скорость 
положительного заряда при
его движении в перекладине под действием напряжённости 
, то получится сила Лоренца 
, направленная против оси и противоположно силе,
перемещающей перекладину.
Если бы перекладина двигалась по
инерции в отсутствие сторонних сил, то в проводящей рамке сила 
привела бы к
торможению движения перекладины и к уменьшению её кинетической энергии. Это
связано с тем, что кинетическая энергия будет трансформироваться в энергию
индукционного тока, выделяемую в виде нагрева проводящей цепи. При разрыве
электрической цепи ток в рамке будет отсутствовать, электрическое поле создаст в перекладине
разность потенциалов, равную электродвижущей силе , и перекладина сможет двигаться с некоторой постоянной
скоростью даже в отсутствие сторонних сил.
В общем
случае рассматриваемый контур или рамка могут быть непроводящими и в них могут
отсутствовать не только свободные, но и связанные заряды. Тогда объяснение
эффекта индукции на основе силы Лоренца согласно (38-39) становится
неприменимым, хотя в движущейся перекладине всегда возникает циркуляция
электрического поля и соответствующая электродвижущая сила. Следовательно,
требуется иное, более общее объяснение, например, основанное на преобразовании
компонент электрического и магнитного полей из системы отсчёта 
, связанной с неподвижной рамкой, в систему отсчёта 
, связанную с движущейся перекладиной.
Электрическое поле 
и магнитное поле 
входят в компоненты
тензора электромагнитного поля и потому преобразуются по тензорному закону. При
движении произвольной точки на перекладине вдоль оси 
на рисунке 1
компоненты полей в данной точке в рамках специальной теории относительности
преобразуются так:
, 
, 
,
, 
, 
. (40)
Величина
есть фактор Лоренца
для скорости 
движения перекладины.
Поскольку
в 
поле 
, поле 
, то в будут только следующие
ненулевые компоненты полей: 
, 
. Следовательно, наблюдатель, движущийся в вместе с перекладиной,
должен обнаружить циркуляцию электрического поля в виде
.
(41)
Из
сравнения (37) и (41) следует, что 
. Вклад в электродвижущие силы 
и 
делают только
электрические поля 
и 
, соответственно. Это отличает электродвижущую силу от
электрического потенциала 
, поскольку в силу определения 
поле 
связано не только с , но и с векторным потенциалом 
. Однако в рассматриваемом случае магнитное поле 
не зависит от времени,
и поскольку 
, то не зависит от времени и 
, не давая вклад в электрическое поле. Именно поэтому
согласно (30) электродвижущая сила 
ведёт себя аналогично 
.
Рассмотрим
теперь, как должен преобразовываться электрический потенциал из в систему отсчёта . Если в 
имеется 4-потенциал
электрического поля 
, а движется в вдоль оси 
, то согласно преобразованиям Лоренца для 4-векторов
получится следующее:
, 
, 
, 
.
Пользуясь
свободой выбора векторного потенциала, связанной с калибровкой 4-потенциала в
виде 
в плоском
пространстве-времени Минковского, в можно
положить, что 
, 
, 
, где 
. Это для компонент 4-потенциала в даёт:
, 
, 
, 
.
Соотношение
для потенциала получается аналогичным
соотношению 
для электродвижущей силы,
полученном выше. Таким образом, проводя аналогию между электродвижущей силой и
электрическим скалярным потенциалом, можно объяснить закон электромагнитной
индукции для случая увеличения площади рамки, не используя силы Лоренца, а
опираясь на преобразование компонент полей между двумя системами отсчёта.
6.
Анализ интегральной теоремы о циркуляции магнитного поля
Поскольку
интегральная теорема о циркуляции магнитного поля по неподвижному контуру 
в (10)
доказывается с помощью
теоремы Кельвина-Стокса, то не исключено, что как и в случае с эффектом электромагнитной индукции,
доказательство может не дать полного описания явления. Уравнение (10)
утверждает, что циркуляция магнитного поля возникает при наличии
перпендикулярной компоненты электрического тока сквозь неподвижный контур, а
также в случае изменения во времени электрического поля, пересекающего контур.
Однако из теоремы о дивергенции (22) вытекает интегральное уравнение (23), более полно описывающее теорему о циркуляции магнитного поля. Это уравнение в рамках специальной теории относительности можно переписать так:
,
(42)
где
есть поток
напряжённости электрического поля через поверхность 
, ограниченную контуром 
.
Согласно (42), циркуляция
магнитного поля может появиться в отсутствие электрического тока 
и при постоянном
электрическом поле, если будет изменяться площадь контура, пересекаемого
электрическим полем. Последнее изменяет поток 
в (42). Данный вывод
не может быть предсказан с помощью
теоремы Кельвина-Стокса, ввиду ограниченности её действия.
Для
анализа ситуации снова обратимся к рисунку 1, где заменим магнитное поле 
на электрическое поле 
. Выберем направление обхода рамки против часовой стрелки,
тогда для левой части (42) можно записать:
.
Считая,
что электрический ток 
сквозь рамку равен
нулю, найдём правую часть (42):
, 
.
Как
следствие равенства левой и правой части (42), приходим к соотношению 
. Мы не можем объяснить это соотношение рассуждениями на
основе силы Лоренца, как это было для электромагнитной индукции в (38). Это тем
более справедливо тогда, когда в выбранном контуре вообще отсутствуют
электрические заряды. Единственным оставшимся способом объяснения является
преобразование компонент полей из 
в 
. Полагая 
, 
в , из (40) находим в 
следующие ненулевые
компоненты полей: 
, 
. Сравнение с выражением для 
даёт: 
. Заметим, что из (37) и (41) следует подобное равенство 
для случая
электромагнитной индукции.
У нас получается некоторое противоречие в том,
что изначально мы считали 
везде в , однако при расчёте циркуляции магнитного поля в (42)
появляется некоторое магнитное поле внутри движущейся
перекладины. Чтобы избежать противоречия, правильнее будет считать, что на
самом деле внутри перекладины в её системе отсчёта присутствует
магнитное поле 
, создающее циркуляцию в перекладине. А в системе отсчёта данная циркуляция
проявляется уже как циркуляция эффективного магнитного поля 
.
7. Что даёт калибровка
4-потенциала?
В предыдущих разделах мы рассмотрели потоки и
циркуляции электрического и магнитного полей, являющихся компонентами тензора
электромагнитного поля. Существует ещё одна величина, характеризующая
электромагнитное поле – это 4-потенциал , где компоненты 4-потенциала содержат скалярный потенциал 
и векторный потенциал . В (27) для 
была определена
циркуляции 
по неподвижному
контуру, но оказывается, что можно ещё определить поток 
через замкнутую
поверхность.
Начнём с того, что в ковариантной калибровке Лоренца
4-потенциал должен удовлетворять соотношению:
.
Умножим
данное равенство на ковариантный элемент 4-объёма 
, возьмём интеграл по 4-объёму и используем теорему о
дивергенции в четырёхмерном виде:
,
где 
есть ортонормированный
дифференциал 
трёхмерной
гиперповерхности, окружающей физическую систему в четырёхмерном пространстве, 
есть четырёхмерный
вектор нормали, перпендикулярный гиперповерхности и направленный наружу.
Последнее равенство можно записать более
подробно:
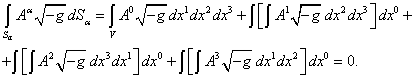
Продифференцируем
данное равенство по переменной 
, где 
– координатное время:
Здесь три интеграла по площади в сумме дают
интеграл по замкнутой двумерной поверхности, окружающей рассматриваемый
трёхмерный объём:
,
(43)
где 
есть ортонормированный
элемент двумерной поверхности; 
представляет собой
поток потенциалов электромагнитного поля через замкнутую. поверхность; индексы 
и не совпадают друг с
другом; величина 
есть интеграл по
объёму от скалярной компоненты 4-потенциала и может быть названа интегральным
скалярным потенциалом.
Так как 
, 
, то компоненты 
4-потенциала являются
функциями скалярного и векторного потенциалов электромагнитного поля.
В пределе специальной теории относительности 
, для декартовых координат будет 
, 
, и (43) упрощается:
.
(44)
В этом случае видно, что 
становится потоком
векторного потенциала 
по замкнутой
поверхности. Поток 
может появляться по
двум причинам – если меняется во времени распределение скалярного потенциала внутри
рассматриваемого объёма, либо если меняется величина самого объёма. Согласно
(44), изменение во времени может привести
к появлению в пространстве векторного потенциала , и если будет зависеть от
времени, то от этого появляется ещё дополнительное электрическое поле согласно
определения 
.
8. Заключение
С помощью теоремы о дивергенции мы получили четырёхмерное уравнение (19), из которого следует
интегральная теорема Гаусса (20) в ковариантной форме. Поток
электромагнитного поля через замкнутую поверхность в (20) определяется
следующим образом: 
, где индексы 
и не совпадают друг с
другом. В пределе специальной теории относительности поток 
переходит в поток
электрического поля без добавок от компонент магнитного поля.
Из (19) также получается интегральная
теорема о циркуляции магнитного поля в виде (22). При этом показывается, что
если толщина рассматриваемого объёма стремится к нулю, то (22) переходит в
интегральное уравнение (23), обобщающее трёхмерную теорему Кельвина-Стокса.
Аналогично из четырёхмерного ковариантного
уравнения (32) следуют интегральная теорема Гаусса для магнитного поля (33) и
интегральный закон электромагнитной индукции Фарадея (35). В отличие от
трёхмерного подхода, ковариантное выражение для магнитного
потока через поверхность 
включает в себя
определитель 
метрического тензора: 
.
Меняется
и выражение для электродвижущей силы: 
. Согласно (30), электродвижущая сила с точностью до
множителя 
ведёт себя как
потенциал: 
.
Сравнение (29) и (33), (28) и (35) показывает,
что четырёхмерная теорема Кельвина-Стокса (24) представлена в рамках специальной теории
относительности и её следует заменить на выражение в ковариантной записи (25).
Однако для согласования уравнений (28) и (35) необходимо предполагать, что в
(25) определитель 
метрического
тензора не зависит от времени. Кроме того, уравнение (28) представляет закон электромагнитной индукции лишь для неподвижного
контура с постоянной площадью. Получается, что четырёхмерная теорема Кельвина-Стокса даже в виде (25) не позволяет
описать полностью закон электромагнитной индукции – для этого требуется
применение теоремы о дивергенции к дуальному тензору электромагнитного поля,
которое приводит к (35). Таким образом, теорема Кельвина-Стокса оказывается излишней при
выводе интегральных уравнений электромагнитного поля.
Однако положительной стороной теоремы
Кельвина-Стокса является то,
что из неё непосредственно получается уравнение (27), в котором поток
магнитного поля 
через некоторую
фиксированную поверхность 
приводит к циркуляции векторного потенциала по неподвижному
контуру, окружающему данную поверхность. Кроме того, становится видно, что
изменение потока магнитного поля через контур с постоянной площадью приводит к
вихревому электрическому полю в контуре вследствие изменения во времени
векторного потенциала.
Кроме
циркуляции, векторный потенциал имеет и поток
согласно интегральным уравнениям (43-44). При этом поток потенциала сквозь замкнутую
поверхность появляется лишь тогда, когда возникает изменение во времени новой
физической величины – интегрального скалярного потенциала 
.
Полученные интегральные уравнения были
применены для описания стандартного опыта с рамкой, в которой имеется
движущаяся перекладина, позволяющая изменять площадь рамки и поток магнитного
или электрического поля через рамку. Как правило, в подобных опытах знаки
потоков полей по площади контура и циркуляции полей по контуру определяются
правилом правого буравчика и правилом Ленца, соответственно. Если же исходить
из четырёхмерного подхода и уравнений (19) и (32), то знаки потоков и
циркуляции устанавливаются автоматически.
Анализ опыта в отношении электромагнитной
индукции при изменении площади в магнитном потоке показывает неполноту подхода,
опирающегося на силу Лоренца для объяснения возникновения электродвижущей силы.
Такой подход оказывается вообще неприменимым в случае, когда в рамке при
изменении площади меняется поток электрического поля, приводя к циркуляции
магнитного поля в контуре. Единственным подходом, позволяющим одновременно
объяснить опыты с изменением потоков магнитного и электрического полей при
изменении площади контура, оказывается пересчёт компонент тензора
электромагнитного поля из неподвижной системы отсчёта 
в систему отсчёта 
,
связанную с движущейся стороной контура (с движущейся перекладиной в случае
рамки на рисунке 1). При этом появляющаяся в 
циркуляция магнитного или электрического поля
проявляется в 
как циркуляция
некоторого эффективно действующего поля, как манифестация соответствующего
эффекта в 
.
Так, в ситуации на рисунке 1 изначально нет
электрического поля и имеется только постоянное магнитное поле. Но как только
перекладина начинает движение, в ней с
точки зрения появляется вихревое электрическое поле 
, приводящее к циркуляции этого поля. Фактически же в перекладине
в её системе отсчёта возникает поле 
и соответствующая
циркуляция, а также электродвижущая сила 
, которая в выглядит как 
. Отсюда следует вывод, что эффекты от вихревых электрических
и магнитных полей в движущейся части контура с точки зрения имеют своей причиной
аналогичные эффекты в данной части контура, когда они имеют место с точки
зрения сопутствующей системы отсчёта .
Если исходить из (10), циркуляция магнитного
поля в контуре может возникать при изменении во времени потока электрического
поля за счёт изменения величины самого электрического поля. Это является
следствием применения теоремы Кельвина-Стокса к неподвижному контуру. Однако
применение четырёхмерного подхода с помощью теоремы о дивергенции согласно
(22-23) приводит к новому эффекту в (42), согласно которому циркуляция
магнитного поля в контуре может возникать ещё при изменении во времени потока
электрического поля за счёт изменения величины площади, ограниченной контуром.
Список использованных источников
1. Feynman R.P., Leighton R.B. and Sands M.L. The Feynman Lectures on
Physics. San Francisco: Pearson/Addison-Wesley (2006). Vol. 2. ISBN 0805390499.
2.
Simonyi K.
Theoretische Elektrotechnik (5th ed.). Berlin: VEB Deutscher Verlag der
Wissenschaften (1973).
3. Thorne K.S., Macdonald D. Electrodynamics in curved space-time: 3+1 formulation. Monthly Notices of the Royal Astronomical Society, Vol. 198, pp. 339-343 (1982). https://doi.org/10.1093/mnras/198.2.339.
4. Tsagas C.G. Electromagnetic fields in curved spacetimes. Class. Quantum
Grav. Vol. 22 (2), pp. 393-407 (2005). https://doi.org/10.1088/0264-9381/22/2/011.
5. Cabral F., Lobo F.S.N. Electrodynamics and Spacetime Geometry:
Foundations. Foundations of Physics, Vol. 47(2), pp. 208-228 (2017). http://dx.doi.org/10.1007/s10701-016-0051-6.
6. Sorkin R. The quantum electromagnetic field in multiply connected space.
Journal of Physics A: Mathematical and General, Vol. 12, No. 3, pp. 403-422
(1979). https://doi.org/10.1088/0305-4470/12/3/016.
7. Landau L.D.,
Lifshitz E.M. The Classical Theory of Fields. Pergamon Press (1951). ISBN 7-5062-4256-7.
8. Дирак
П. А. М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с. Dirac P. A. M. General Theory of Relativity,
Princeton University Press (1975). ISBN
0-691-01146-X.
Источник: http://sergf.ru/cr.htm