Уравнения гравитационного поля в теории относительности

Федосин С.Г., Ким А.С.

intelli@list.ru

В отличие от аксиоматики общей теории относительности гравитация в инерциальных системах отсчёта рассматривается как реальное поле, характеризующееся соответствующими потенциалами, ковариантными уравнениями поля и лоренц-инвариантностью. При переходе к неинерциальным системам отсчёта за счёт присутствия вещества и плотности энергии поля метрический тензор становится отличным от метрического тензора пространства Минковского, а физические явления меняют свой вид. В этом случае тяготение как воздействие на расстоянии можно представить как интегральный эффект взаимодействия тел друг с другом посредством гравитационного и электромагнитного полей.

В соответствии с устоявшейся традицией считается, что пространство-время вблизи гравитирующих тел искривлено, является неевклидовым и описывается с помощью общей теории относительности (ОТО), в то время как специальная теория относительности (СТО) имеет дело с плоским пространством-временем Минковского. В ОТО все системы отсчёта по определению являются неинерциальными, поскольку каждая масса как бы генерирует вокруг себя поле, меняющее свойства пространства-времени от точки к точке. Решение основного уравнения ОТО для метрики, уравнения Эйнштейна-Гильберта, в случае слабого поля вблизи тяготеющего тела даёт поправку к компоненте метрического тензора, которая интерпретируется как скалярный гравитационный потенциал. Гравитационное ускорение получается как градиент этого потенциала, взятый с обратным знаком, в результате мы приходим к классическому закону Ньютона. В отличие от гравитационного электромагнитное поле является несколько более фундаментальным – оно лоренц-инвариантно, преобразуется по известным законам в любых системах отсчёта, всегда обладает определёнными скалярным и векторным потенциалами и даёт свой собственный вклад в метрику. Целью данной работы является построение лоренц-инвариантной теории гравитационного поля (ЛИТГ) как настоящего физического поля, участвующего наравне с веществом и другими полями в образовании метрических свойств пространства-времени.

Как известно, явления в неинерциальных системах отсчёта можно рассматривать и из инерциальных систем отсчёта, вводя силы инерции или соответствующие гравитационные силы. В противоположность подходу, принятому в ОТО, будем считать потенциал поля первичным понятием, а плотности энергии и импульса вещества и поля – ответственными за отклонение наблюдаемой метрики пространства- времени от метрики пространства Минковского.

Скалярный гравитационный потенциал в инерциальной системе отсчёта _, связанной с телом, имеет вид:

где координаты задают точку, где измеряется потенциал, M - масса гравитирующего тела, - гравитационная постоянная. Расчёт скалярного потенциала этого же гравитационного поля в инерциальной системе отсчёта S , в которой тело движется со скоростью V, может быть осуществлён двумя способами. По одному из них используется общее решение Льенара и Вихерта [1] для запаздывающего поля, что даёт следующее:

(1)

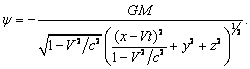
Формулу (1) можно получить и с помощью лоренцевского преобразования из системы отсчёта в S с помощью 4-вектора потенциала , в котором кроме скалярного потенциала находится гравитационный векторный потенциал :

.

Векторный потенциал согласно [2] дополняет потенциал до 4-вектора и учитывает изменение гравитационного поля за счёт любого движения массы и запаздывания гравитационного взаимодействия. Точно также векторный потенциал в электродинамике ответственен за возникновение электромагнитного поля даже в том случае, когда скалярный потенциал равен нулю из-за компенсации положительных и отрицательных зарядов [3].

Приравнивая дивергенцию контравариантного 4-потенциала к нулю, с помощью метрического тензора находим калибровочное условие для потенциалов в СТО:

Антисимметричный тензор гравитационного поля можно построить из ковариантного 4-потенциала :

.

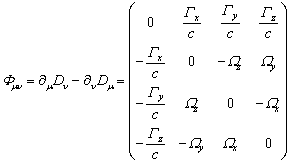Компонентами тензора являются напряжённость гравитационного поля и поле кручения , выражающиеся через потенциалы следующим образом:

Умножая плотность массы в покоящейся системе отсчёта на 4-вектор скорости , получим массовый 4-ток:

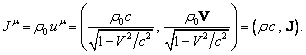
Действие четырёхмерного даламбертиана на 4-потенциал даёт вектор, пропорциональный 4-току :

(2) □²

Уравнения (2) являются волновыми уравнениями для потенциалов и гравитационного поля, а их решения имеют вид:

здесь потенциалы в точке 1 в момент времени t находятся путём интегрирования распределения масс (массовых токов) в области с объёмом в более ранний момент времени - текущее расстояние между точкой 1 и элементами объёма в момент времени , c - скорость распространения гравитационного воздействия.

Уравнения гравитационного поля получаются путём дифференцирования тензора :

(3)

В раскрытом виде уравнения (3) содержат векторы и :

,

(4)

,

Если определить гравитационную силу выражением , где m - инвариантная масса частицы, то уравнение движения частицы в гравитационном поле в рамках СТО можно записать так:

здесь и - контравариантный и ковариантный 4-импульсы частицы соответственно,

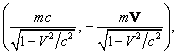
- дифференциал собственного времени частицы, - интервал.

Как показывает расчёт в [2], при параллельном движении двух масс за счёт векторного потенциала и соответствующего ему поля кручения между массами возникает сила отталкивания. Данная сила при большой скорости движения масс вычитается из силы гравитационного притяжения таким образом, что при достижении скорости света суммарная сила между массами стремится к нулю: , здесь - сила притяжения между покоящимися массами. Одновременно интервалы времени движущихся относительно лабораторной системы отсчёта часов согласно СТО будут длиннее: 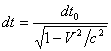. Приращения поперечных относительно движения импульсов масс в лабораторной и сопутствующей системах отсчёта оказываются одинаковыми: , что как раз и следует из СТО.

На основе тензора и метрического тензора можно построить тензор плотности энергии-импульса гравитационного поля:

(5)

Компонента в тензоре (5) представляет собой плотность энергии гравитационного поля:

а компоненты , умноженные на скорость c , дают вектор плотности потока энергии поля . Плотность энергии поля и вектор связаны между собой:

Смысл этого соотношения заключается в том, что поток энергии в некоторый объём через его поверхность приводит к увеличению гравитационной энергии в этом объёме и (или) к совершению работы по ускорению вещества.

Приведённые расчёты показывают, что в инерциальных системах можно построить самосогласованную лоренц-инвариантную теорию гравитационного поля, в соответствии с уравнениями (4) справедливую вплоть до релятивистских скоростей движения тел. Следовательно, уравнения гравитационного поля с помощью метрического тензора можно записать и в ковариантном виде. Так, согласно [4] в уравнении для метрики в тензор плотности энергии-импульса рассматриваемой физической системы следует включить тензор , содержащий согласно (5) не только напряжённость поля , но и поле кручения гравитационного поля :

(6)

здесь - тензор Риччи, R - скалярная кривизна, - некоторая константа порядка единицы, - тензоры плотности энергии-импульса поля ускорений, поля давления, электромагнитного поля и гравитационного поля соответственно. Решениями уравнений (6) являются зависимости компонент метрического тензора от координат и времени, показывающие отклонение от метрического тензора пространства Минковского.

Уравнения движения частиц вещества находятся из равенства нулю ковариантной производной от тензора плотности энергии-импульса рассматриваемой физической системы:

(7)

Поскольку в (7) в тензоре находится кручение , то решения этого уравнения приобретают некоторые добавки, существенные при больших скоростях. Однако в условиях Солнечной системы и обычных скоростях движения тел поправки к метрическому тензору оказываются весьма незначительными. В [2] рассмотрена метрика внутри и за пределами однородного по плотности массивного сферического тела с учётом вклада от гравитационного поля. Было найдено, что в дополнение к метрике Шварцшильда, содержащей члены вида , появляются также члены второго порядка малости, содержащие в знаменателе с⁴ . Практически все тесты ОТО – смещение перигелия Меркурия, искривление лучей света и задержка их распространения в гравитационном поле Солнца, изменение частоты света при распространении между точками с разными гравитационными потенциалами и другие аналогичные опыты подтверждены только на уровне первого порядка. По-видимому, увеличение точности измерений со временем позволит повести проверку как ОТО, так и предлагаемого нами подхода.

Обычно полагают, что в ОТО тяготение описывается как воздействие материи на свойства пространства-времени, которые в свою очередь влияют на движение тел. В свете вышеизложенного данное положение переформулируется в том смысле, что изменение количества вещества, электромагнитного и гравитационного полей изменяет как свойства пространства-времени, отмечаемые наблюдателем, так и видимые траектории движения тел. Таким образом, хотя тяготение формально можно сводить к искривлению пространства-времени и метрики под действием всевозможных источников энергии вещества и поля, но в то же время гравитацию следует считать самостоятельным физическим полем, которое вместе с движущимся веществом и электромагнитным полем задаёт метрику в заданной точке и определяет движение тел. Отличие гравитации от тяготения тогда заключается в том, что последнее есть интегральный эффект от действия гравитационных и электромагнитных полей, связанных соответственно с тяготеющими массами и заряженными телами.

Литература

[1] Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Том 6.

М.: Мир, 1977. / перевод с англ. Feynman R., Leighton R., Sands M. The Feynman

lectures on physics. V.2. Addison-Wesley Publishing Company, Inc. Reading,

Massachusetts, Palo Alto. London. 1964.

[2] Федосин С. Физика и философия подобия от преонов до метагалактик. Пермь:

Стиль-МГ, 1999.

[3] Ландау Л. Д. , Лифшиц Е. М. Теоретическая физика. Т.2. Теория поля. М.: Наука,

1988.

[4] Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. vixra.org, 5 Mar 2014.

Источник: http://sergf.ru/ur.htm

На научный сайт