Известия вузов. Физика, 2002, Т. 45, №. 5, С. 93 – 97.
http://www.ntl.tomskinvest.ru/article_2002.html
УДК 539.12
С.Г. Федосин, А.С. Ким
Момент импульса и
радиус протона
С помощью теории ядерной гравитации вычисляется момент импульса гравитационного поля протона и сравнивается с соответствующим результатом для момента импульса электромагнитного поля. В результате делается оценка радиуса протона и устанавливается соотношение для момента импульса поля, совпадающее по форме с теоремой вириала для энергии.
Протон как квантовый объект обладает присущими ему магнитным моментом, электрическим зарядом, спином, массой и другими характеристиками, которые с большой точностью измеряются во множестве экспериментов физики элементарных частиц. Очевидно, что многие параметры протона могут быть связаны друг с другом какими-либо соотношениями, вытекающими из физической природы взаимодействий. Характерными примерами являются пропорциональность между магнитным моментом, спином и удельным зарядом, наблюдаемая для большинства элементарных частиц, и пропорциональность между спином и квадратом массы частиц на траекториях Редже. В квантовой хромодинамике предполагается, что целостность протона осуществляется благодаря сильному взаимодействию между тремя составляющими его кварками и квантами поля – глюонами. Другой подход вводит в рассмотрение ядерную гравитацию [1] по аналогии с обычной гравитацией, когда целостность космических объектов оказывается следствием баланса притягивающих гравитационных сил и электромагнитных сил отталкивания частиц вещества. В данной работе с помощью теории гравитационного поля накладывается условие на момент импульса протона и делается оценка его радиуса.
Скалярный гравитационный потенциал внутри протона для случая однородного по плотности распределения вещества с учётом граничных условий имеет вид:
при условии,
что 
здесь 
- постоянная ядерной гравитации,
-
плотность вещества протона,
r - текущий радиус,
R, M - радиус и масса протона соответственно.
Ускорение вещества G под действием поля в статическом случае определяется через градиент потенциала:
(1)
где M(r) - масса вещества внутри радиуса r .
При вращении протона гравитационное поле приобретает момент импульса, объёмная плотность которого согласно [1] находится по формуле:
(2)
где W - кручение гравитационного поля.
Для оценки кручения внутри протона произведём мгновенное лоренцевское преобразование тензора гравитационного поля, компонентами которого являются компоненты векторов G/c и W, из покоящейся системы отсчёта S¢ в движущуюся со скоростью V вдоль оси x систему отсчёта S . Поскольку кручение W в S¢ равно нулю, то пренебрегая лоренцевским фактором, для системы отсчёта S находим:
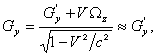
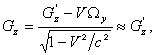(3)
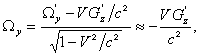
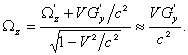
В силу относительности движения в системе отсчёта S протон также движется со скоростью V, но в обратном направлении. Если
сделать преобразование из системы отсчёта
S¢ в S
в каждой точке внутри протона, то линейную скорость V можно выразить через
угловую скорость вращения w и сферические координаты r , q , j в виде соотношения 
, а (1) и (3) переписать следующим образом:
(4)
При не очень больших скоростях можно не учитывать добавки в компоненты поля (4),
которые возникают из-за того, что
на самом деле надо
делать преобразования не в локально инерциальных, а во вращающихся вдоль
оси z системах отсчёта. Согласно
(4) при вращении протона против часовой стрелки внутреннее кручение 
везде направлено
против оси z , а проекции кручения W на плоскости z = const направлены от
оси z
наружу. С помощью (2) находим компоненты вектора плотности импульса
гравитационного поля внутри протона:
Вектор g направлен в ту же сторону, что и линейная скорость
вращения единичных объёмов вещества протона. Для того,
чтобы подсчитать момент импульса гравитационного поля внутри протона, нужно
модуль вектора g умножить
на расстояние до оси z , то есть на величину 
, а затем проинтегрировать по объёму протона:
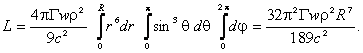
Учитывая выражения для массы протона 
и его спина 
для случая однородного
распределения вещества,
величину L можно записать в таком
виде:
(5)
причём вектор L направлен вдоль спина I .
Будем считать, что в каждом гравитационном поле есть только один тип вырожденных объектов, имеющих максимальную плотность вещества и соответственно наибольшие напряжённости гравитационного и электромагнитного полей. Для ядерной гравитации такими объектами являются нуклоны, для обычной гравитации – нейтронные звёзды. Тогда следует ожидать, что в (5) момент импульса L гравитационного поля равняется спину протона I . В самом деле, если бы оказалось, что L > I , то тогда само гравитационное поле стало бы раскручивать протон, увеличивая его спин. Аналогично электромагнитное давление на вещество направлено вдоль вектора плотности импульса электромагнитного поля и пропорционально энергии поля, поглощённой веществом. Сокращая величины L и I в (5), можно оценить радиус протона:
(6)
Постоянная ядерной гравитации в (6)
находится из условия равенства гравитационной и электростатической сил в
атоме водорода на радиусе Бора 
:
(7)
причём 
-
элементарный электрический заряд,
-
электрическая постоянная,
-
массы протона и электрона соответственно.
Для сравнения с результатом (6) приведём другие способы определения радиуса протона из [1]. Нейтрон и протон составляют вместе изотопический дублет и очень близки друг к другу по своим свойствам. Разницу масс между электрически нейтральным нейтроном и протоном, имеющим заряд e , можно приписать массе-энергии от электрического поля протона:
Принимая K = 0,6
как для однородно заряженного шара, подставляя массу нейтрона 
и скорость света c , находим радиус протона 
При объяснении
волн де Бройля, сопровождающих движущиеся частицы, через внутренние колебания
электромагнитного поля, было найдено соответствующее условие на размеры частиц.
Для протона получается: 
здесь h -
постоянная Планка.
Экспериментально определённые значения радиуса протона
достаточно близки к величине (6). При этом как правило
определяется среднеквадратичный зарядовый радиус 
, который может быть больше, чем R .
Так, в опытах по рассеянию электронов на протонах [2] нашли 
Согласно [3],
установившееся при энергиях более 10 Гэв сечение
взаимодействия нуклонов друг с другом составляет 38 мбарн.
В классическом пределе можно считать, что это сечение близко к геометрическому
сечению сталкивающихся частиц, то есть к величине 
. Тогда 
Равенство (7) позволяет установить определённое соотношение между гравитационной и электромагнитной энергиями в протоне. Для энергий можно записать:
где 
-
коэффициенты, зависящие от распределения массы или заряда соответственно; для
случая однородного распределения 
. Полагая 
, с помощью (7) получаем:
,
то есть отношение гравитационной энергии к электростатической энергии приблизительно равно отношению масс протона и электрона.
Вернёмся теперь назад к соотношению (5) с тем, чтобы
подкрепить вывод о равенстве момента импульса гравитационного поля внутри
протона и его спина. Предположим, что
заряд протона равномерно распределён по объёму радиуса R ,
а магнитный момент 
сосредоточен в центре
и направлен вдоль оси z. Для расчёта плотности импульса
электромагнитного поля за пределами протона при
r
> R используем следующие
обычные выражения:
где E - напряжённость электрического поля,
B - индукция магнитного поля,
-
магнитная постоянная.
Вектор 
везде лежит в
плоскостях z = const
, перпендикулярен оси z и вращается против
часовой стрелки, а для его модуля в сферических координатах можно записать:
Момент импульса электромагнитного поля за пределами протона
определяется интегралом по объёму от 
до бесконечности:
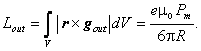
Напряжённость электрического поля внутри однородно заряженного протона, модуль вектора плотности импульса и момент импульса поля будут иметь вид:
, 
,
где e(r) - заряд внутри радиуса r .
Мы получили, что момент импульса электромагнитного поля внутри протона в 2 раза меньше момента импульса вне объёма протона:
.
(8)
Кроме этого, закон сохранения момента импульса связывает
механический момент импульса 
движущихся внутри
протона зарядов, создающих его магнитное поле, и суммарный момент импульса
электромагнитного поля 
:
(9)
Если считать, что магнитный момент протона сосредоточен в
его центре и направлен вдоль оси z , то из (8), (9)
следует, что направление 
противоположно 
, а магнитное поле протона как будто образуется от движения
отрицательных зарядов по часовой
стрелке относительно оси z . При этом должно выполняться равенство
.
В другом противоположном случае магнитный момент расположен не в самом центре протона, а равномерно распределён по всему его объёму. Среди известных объектов ближайшим аналогом протона является нейтронная звезда, магнитное поле которой, плотность вещества и степень его вырождения ненамного слабее, чем у протона. В нейтронной звезде магнитное поле должно быть вморожено в вещество, поддерживаясь упорядоченным состоянием магнитных моментов нейтронов, у которых магнитный момент и спин направлены противоположно. Представим мысленно, что магнитный момент протона, который ранее мы считали расположенным в центре, теперь занимает весь объём таким образом, чтобы оставить без изменения амплитуды магнитного поля и внутри и снаружи протона. Тогда картина магнитного поля за пределами протона не изменится, однако внутри магнитное поле поменяет знак и вместо (8), (9) получится:
(10)
Независимо от характера распределения магнитного момента в объёме протона его полный магнитный момент оказывается противоположным по направлению механическому моменту импульса частиц, создающих магнитный момент. Это же справедливо и для нейтронных звёзд, так что протон и нейтронная звезда приобретают ещё один признак подобия.
Если попарно сопоставить электрические и гравитационные
величины и I , 
и L , то из (10) как раз
вытекает равенство момента импульса вращающихся масс протона или его спина величине момента импульса
гравитационного поля внутри
протона: I = L , что и было использовано в (5) для оценки радиуса протона.
Поскольку аналогично (9) сумма момента импульса вращающегося протона и полного момента
импульса его гравитационного поля должна быть равна нулю, то каждая передача
вращательного момента при взаимодействиях должна сопровождаться и
соответствующей передачей момента импульса поля.
В соответствии с вышеизложенным,
для случая однородного распределения источников магнитного поля или массы
внутренний момент импульса электромагнитного или соответственно гравитационного
поля с точностью до знака равен половине момента импульса поля за пределами
объекта. Соотношение (10) замечательным образом перекликается с известной
теоремой вириала, согласно которой работа сторонних сил по созданию объекта
осуществляется таким образом, что половина затраченной энергии переходит в
кинетическую энергию частиц объекта, а другая половина переходит в энергию поля
и обычно уносится излучением.
Список литературы
1. Федосин С. Физика и философия подобия от преонов до метагалактик.- Пермь: Стиль-МГ, 1999. -544 с.
2. Хофштадтер Р.// Сб.: Физика атомного ядра. - М.: ГИФМЛ, 1962. - С.72-86.
3. Барашенков В.С. Сечения взаимодействия элементарных частиц. - М.: Наука, 1966. -531 с.
Пермский государственный университет Ноябрь 2000 г.
Источник:
http://sergf.ru/mo.htm