На русском языке

OALib Journal, Vol. 3, P. 1-15 (2016). http://dx.doi.org/10.4236/oalib.1102459

 

The concept of the general force vector field

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Russia

E-mail: intelli@list.ru

 

A hypothesis is suggested that the fields associated with macroscopic bodies, such as classical electromagnetic and gravitational fields, acceleration field, pressure field, dissipation field, strong interaction field and weak interaction field, are the manifestations of a single general field. Using the generalized four-velocity as the four-potential of the general field, with the help of the principle of least action it is shown that each of these seven fields contributes linearly to the formation of the total four-force density. The general field equations, equation of the particles’ motion in this field, equation for the metric and the system’s energy are determined. It should be noted that the stress-energy tensor of the general field includes not only the stress-energy tensors of these seven fields, but also the cross terms with the products of various field strengths. As a result, the energy and momentum of the system with several fields can differ from the classical values, not taking into account such cross terms in the general field energy and momentum.

Keywords: general field; generalized velocity; acceleration field; pressure field; dissipation field.

PACS Nos.: 03.50.x, 12.10.–g.

 

1. Introduction

Many scientists believe that there is generality between the fields known in physics which is not fully understood so far. So in the “Grand unified theory” in order to describe elementary particles in unified quantum-field formalism an attempt is made to combine strong, weak and electromagnetic interactions [1]. In the “Theory of everything” gravitational interactions are also taken into account. However, so far there is incompatibility between the general theory of relativity, describing gravitation at the macroscopic level, and the quantum field theory, describing interaction of particles at the microscopic level [2].

One of the well-known models of unification of gravitation and electromagnetism is the Kaluza-Klein theory [3-4]. This theory uses five-dimensional spacetime and some scalar field, and the theory’s consequences are the equations equivalent to Maxwell equations and the equations of general theory of relativity.

Besides fundamental interactions, there are other fields that influence directly the matter particles and transfer energy and momentum. These fields include the acceleration field and pressure field [5], as well as the field of energy dissipation due to viscosity [6]. Under the influence of these fields almost uniform spatial and temporal distribution of velocities, pressure, energy dissipation, potentials and field strengths takes place in bodies, which arises from the wave equation of a standard form. Similarity of distribution of physical functions indicates a single mechanism of their generation.

In connection with this, we introduce a concept of a macroscopic general force vector field, in which we include the electromagnetic and gravitational fields, acceleration field, pressure field, dissipation field, strong interaction field, weak interaction field and other vector fields. This general field is assumed to be the main source of acting forces, energy and momentum, as well as the basis for calculation of the system’s metric from the standpoint of non-quantum classical field theory. Including the macroscopic fields of strong interaction and weak interaction in the general field is most necessary in those cases, when reactions of radioactive decay or nuclear fusion take place in massive bodies, as it happens in stars.

 

2. The structure of fields

Table 1 and Table 2 show the notation for the basic functions of each field that we use, including potentials, strengths, energy flux densities and field tensors. The last column of Table 2 shows the notation for the functions of the general field. In the following sections we will provide definitions of each function of the general field, while the definitions of other fields were provided in [5] and [6].

 

Table 1. Field functions

Field

Electromagnetic field

Gravitational field

Acceleration field

Pressure field

Field function

4-potential

Scalar potential

Vector potential

Field strength

Solenoidal vector

Field tensor

Stress-energy tensor

Energy-momentum flux vector

 

Table 2. Field functions

Field

Dissipation field

Strong interaction field

Weak interaction field

General field

Field function

4-potential

Scalar potential

Vector potential

Field strength

Solenoidal vector

Field tensor

Stress-energy tensor

Energy-momentum flux vector

 

In Table 1  is the Poynting vector,  is the Heaviside vector. The stress-energy tensor of the acceleration field  describes the energy and momentum of directed motion of the large-scale substance fluxes, as well as the motion of bodies relative to an arbitrary reference frame or rotation of bodies around a fixed pole. The small-scale and random motion of the matter particles are described by the stress-energy tensor of the dissipation field . We can assume that this tensor characterizes the quantity and flux of internal energy in the form of heat and energy of phase transitions that occur in the system as a result of viscosity. Because of viscosity the directed substance fluxes are decelerated by the surrounding stationary medium and transfer part of their energy to this medium.

The general field is characterized by three three-dimensional vectors and one scalar function: the field strength  and the solenoidal vector  are the components of the tensor , and the scalar potential  and the vector potential  are the components of the 4-potential .

Table 3 shows what field functions and 4-currents are included in these or those equations. It is assumed that the mass 4-current  and the charge 4-current  represent the matter properties, and the properties of fields are specified by the corresponding 4-potential. The field equations are usually divided into two four-dimensional equations – one of them reflects the field’s symmetry and does not contain 4-currents, and the other includes the divergences of field tensors and the 4-currents as the sources that generate the fields.

 

Table 3. Connection between equations, field functions and 4-currents

Field equations and relations

Field functions, 4-currents

Field equations

Divergences of field tensors, 4-currents

Motion equation

Products of field tensors and 4-currents or divergences of fields’ stress-energy tensors

Energy, Lagrangian, Hamiltonian

4-potentials, field tensors and 4-currents

Equation for the metric

The Ricci tensor, scalar curvature, fields’ stress-energy tensors

Gauge of 4-potentials

Divergences of 4-potentials

Continuity equations

Divergences of 4-currents, field tensors, the Ricci tensor

 

We will note that according to Table 3 the stress-energy tensors of fields are present only in the equation for the metric and the equation of the matter motion, but they do not allow us to calculate the system’s energy. As it was shown in [7], the volume integral of the sum of stress-energy tensors of fields gives the integral 4-vector of the system’s field energy-momentum equal to zero. Therefore, the system’s energy is calculated in another way – not as an invariant of the motion equation, but as an invariant conserved over time in the system, in which the Lagrangian does not depend on time [8].

The gauge of 4-potentials allows us to simplify the field equations, especially it is noticeable in the flat spacetime of the special theory of relativity. The continuity equations are obtained as a result of applying the divergence to the field equations with the sources in the form of 4-currents.

 

3. The action function and its variation

Since we are planning to replace all the fields existing in the matter with one general field, the action function will include only the 4-potential of the general field, the tensor of this field and the mass 4-current:

 

                      (1)

 

where  is the Lagrange function or Lagrangian,

 is the scalar curvature,

 is the cosmological constant,

 is the 4-vector of mass (gravitational) current,

 is the mass density in the reference frame associated with the particle,

 is the 4-velocity of a point particle,  is the speed of light,

 is the 4-potential of the general field, described with the scalar potential  and the vector potential  of this field,

 is the general field tensor,

 and  are assumed to be constant coefficients.

 

The 4-potential of the general field is calculated as the sum of 4-potentials of the seven fields and at the same time as a generalized 4-velocity:

 

.                                    (2)

 

Here  is the charge density in the reference frame associated with the particle and we assume that the ratio of the charge density to the mass density is constant. From (2) and the definition of  it follows that the scalar  and vector  potentials of the general field are the sums of the respective scalar and vector potentials of the fields under consideration.

The general field tensor is defined as a 4-curl of the 4-potential :

 

.                                          (3)

 

Assuming that , we substitute (2) into (3):

 

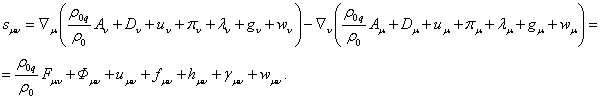
(4)

 

 

In (4) the general field tensor is obtained as the sum of the seven field tensors.

The action function with the terms similar to the terms in (1) was varied in [5]. Using the results obtained there, we will make the appropriate conclusions regarding the general field. For the variation of the action function we can write the following:

 

,                                                  (5)

 

,

 

 

,

 

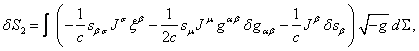
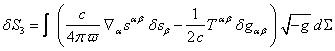where  is the Ricci tensor,

 is the metric tensor variation,

 is an invariant 4-volume, expressed in terms of the time coordinate differential , the product  of the space coordinate differentials, and the square root  of the determinant  of the metric tensor, taken with a negative sign,

 is the variation of coordinates, due to which the variation of the mass 4-current  takes place,

 is the variation of the 4-potential of the general field.

 

The stress-energy tensor of the general field is given by expression:

 

.                                   (6)

 

 

We present some characteristics of the general field in Appendix A.

 

4. The general field equations

Substituting ,  and  in (5) and summing up the terms with identical variations, we obtain the corresponding equations as a consequence of the principle of least action. For example, for the variation  we can write the following:

 

,

 

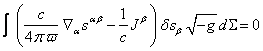          or        .                             (7)

 

Since the general field tensor is defined in (3) using a 4-curl, this tensor is antisymmetric and the following relations hold for it:

 

         or        .                           (8)

 

Equation (8) is the equation of the general field without sources, and equation (7) is the general field equation with the source in the form of mass 4-current.

If we apply the covariant derivative  to (7) we obtain:

 

.                                                    (9)

 

In the flat spacetime the Ricci tensor  becomes zero, the covariant derivative becomes the partial derivative, and the continuity equation acquires its standard form in the special theory of relativity:

 

.                                                           (10)

 

The gauge condition of the 4-potential of the general field:

 

.                                                   (11)

 

We will substitute (2) into (11):

 

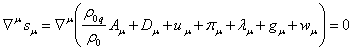.                       (12)

 

If we assume, as in [5-10], that all the fields appear and exist independently of each other, then the gauges of 4-potentials of the fields could also be independent of each other:

 

,                ,              ,          (13)

 

,     ,     ,     .

 

Relations (13) are completely consistent with (12), especially if we assume that the ratio  is constant. But the opposite statement is false in general, since (13) does not follow directly from (12).

We can express (12) in terms of scalar and vector potentials, which are part of the fields’ 4-potentials. In the flat spacetime  can be used instead of , in which case the result is significantly simplified:

 

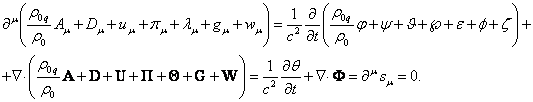
(14)

 

 

 

The gauge of the general field (14) implies a connection between the time derivative of the sum of the scalar potentials and the divergence of the sum of the vector potentials of the seven fields.

 

5. The equation of motion

The term with variation  is present only in  in (5):

 

.

 

Since , then in order to conform to the principle of least action the equation must hold: . This can be written in more detail, if we take into account (4):

 

.                (15)

 

The charge 4-current can be defined with the mass 4-current as follows: , and the tensor product  can be expressed in terms of the 4-acceleration  with the help of the operator of proper-time-derivative:

 

.

 

With this in mind, (15) turns into the four-dimensional equation of motion of viscous compressible substance, which was introduced and analyzed in [6], with addition of the density of 4-forces, arising due to strong and weak interactions:

 

.                        (16)

 

Another way to define the equation of motion is to equate the divergence of the stress-energy tensor of the general field to zero, since the following relation is valid:

 

.                                                  (17)

 

To prove (17) we should expand the tensor  with the help of definition (6), apply the covariant derivative  to the tensor products and then use equations (7) and (8).

If we substitute  from (3) into the left side of (17), the equation of motion could be expressed in terms of the 4-potential  of the general field:

 

.                               (18)

 

On the other hand, we have the relation:

 

.

 

Combining it with the previous equation, we find an equivalent definition of (18):

 

.

 

6. The equation for the metric

After substituting ,  and  in (5) we can distinguish the terms containing the metric tensor variation:

 

.

 

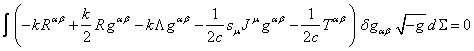Since , the equation for the metric is obtained by equating the expression in brackets inside the integral to zero :

 

.                       (19)

 

Let's contract equation (19) by multiplying by the metric tensor, given that , ,  :

 

.                                                 (20)

 

In [5] we assumed the gauge of the cosmological constant , which according to (2) corresponds to the following expression:

 

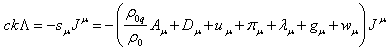.                   (21)

 

Gauge (21) means that the cosmological constant is not an arbitrary quantity. For each substance unit the value  can be chosen so as to equal the total rest energy of all the particles of the substance unit, including the energy of these particles in the potentials of their own internal fields and excluding the energy of the particles’ interaction. The latter can be achieved only when all the particles are separated and scattered at infinity.

With gauge (21), it follows from (20):

 

.                                                            (22)

 

Outside the matter  in (21), then , and the scalar curvature is equal to zero: .

Let us substitute (21) and (22) into (19):

 

.                                             (23)

 

We will obtain the same if we multiply (20) by  and divide by 4 and then substitute in (19).

The equation for the metric (23) coincides with the equivalent equation in [5] and [6], with the difference that in (23) the stress-energy tensor of the general field , due to its definition (6) with regard to (4), contains not only the stress-energy tensors of the seven fields, but also additional cross terms with the products of strengths and solenoidal vectors of these fields.

If we apply the covariant derivative  to (23), the right side becomes zero, as a consequence of the equation of motion in the form of (17). We can apply in the left side of (23) the equality  as the property of the Einstein tensor. We will obtain the equality  or the equivalent equality . If we take into account (21-22), this leads to the following equation, which must hold inside the matter:

 

.

 

The same expression will be obtained in case when the covariant derivative  is applied directly to (19).

 

7. The energy

The energy of the system, consisting of the matter and the fields, can be calculated by the same method as in [5]. If the Lagrangian does not depend on time, the system’s energy will be equal to the Hamiltonian of this system. Taking into account the gauge (21-22), for the energy we obtain the following:

 

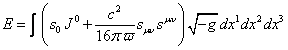.                               (24)

 

The energy (24) depends on the time components of the 4-potential of the general field  and the mass 4-current , and does not depend on the product , where the index  specifies the space components of the 4-vectors. For the 4-momentum of the system we obtain: , where  and  denote the system’s momentum and the velocity of the center of mass.

 

8. Conclusions

Let us compare our approach to unifying the electromagnetic and gravitational fields, acceleration field, pressure field, dissipation field, strong interaction field and weak interaction field with another attempt of unifying the electromagnetic, gravitational and other arbitrary vector fields, which was undertaken by Науменко [11]. His “Unified theory of vector fields” (UTVF) is formulated in the framework of the special theory of relativity. We present here a quote from [11]:

“Let us assume that there are  fields:  each of which has its corresponding charge: .

 It is suggested to consider these fields as manifestations of a single field that conforms to the equations:

 

           ,                 ,                   (25)

 

where  ,  take values from a set of symbols

  () is a matrix of “elrctric constants”,

  () is a matrix of “magnetic constants”,

  () is a matrix of “electrodynamical” constants,

    denotes charge densities,

              denotes current densities.”

 

To these equations Науменко adds the conditions of charge conservation for each field: . As we can see, the equations of UTVF represent extended Maxwell equations. In these equations any field (for example, the electric or magnetic field) can influence the divergence or curl of another field (for example, the gravitational field, torsion field or gravitomagnetic field) or even influence this field’s own divergence or curl.

Науменко also introduces a vector of this unified field:  or , consisting of the sum of strengths and solenoidal vectors of all the fields with the corresponding coefficients. Multiplying equations (25) by the coefficients  and summing over the index , he obtains additional equations:

 

.                              (26)

.                                     (27)

 

In (26) the source of the unified field  is the sum of products of the fields’ charge densities and some coefficients. In (27) the sum of the products of currents and some coefficients gives the curl and the time derivative of the unified field strength . It turns out that the unified field’s divergence is formed of a multitude of available charge densities, and the currents define the curl of the unified field.

The analysis of (25-27) shows that as the basis of the unified field equations of UTVF the idea is taken about the full symmetry of Maxwell-like equations relative to the contribution of charges and currents in the unified field, which is conceived as linear combination of strengths and solenoidal vectors of a set of vector fields.

Our approach differs by the fact that as a basis the 4-potential of the general field  is taken, consisting of the sum of 4-potentials of the seven vector fields. With the help of , by means of antisymmetric covariant differentiation we define the general field tensor  and its invariant . These quantities are substituted into the Lagrangian, and the subsequent use of the principle of least action allows us to derive the necessary equations, including the general field equations, the equation of matter motion in the general field, the equation for calculation of the metric, the stress-energy tensor of the general field. The source of the general field is the mass 4-current , and the contribution of the charge 4-current  in the motion equation or in the energy is revealed when the general field tensor  or the 4-potential  is multiplied by .

According to the method of construction of the 4-potential and the general field tensor, the scalar (vector) potential of the general field consists of the sum of the scalar (vector) potentials of the seven fields. The same can be said about the strength and solenoidal vector of the general field – according to (A12) they consist of the sums of the corresponding vectors of the seven fields.

As we can see in (24), the energy of the system of matter and seven fields in our approach appears to be dependent not only on the stress-energy tensors of these seven fields, but also on the sum of the cross terms with the products of different strengths and solenoidal vectors of the fields.

We remind that the Lorentz-invariant equations of the gravitational field, coinciding by their form with Maxwell equations for the electromagnetic field, first appeared in the works by Heaviside [12]. Subsequently, these equations were derived in a covariant form and became the basis of the covariant theory of gravitation [13]. Later, based on the principle of least action the covariant equations of the acceleration field, pressure field [5] and energy dissipation field [6] were derived. All these equations in the weak field limit have the form of Maxwell equations. According to [7-8], the potentials and strengths of these fields have the same dependence on the coordinates and time, obeying the wave equation. Thus, there is every reason to acknowledge the existence of a single general field, for which the above mentioned seven fields are the particular forms.

In our opinion, this situation is closely connected with the theorem of equipartition of energy. Usually this theorem is interpreted as follows: when the system is in equilibrium, the kinetic energy is distributed between all those degrees of freedom that appear in the energy as quadratic functions. Apparently, this definition should be expanded so that the energy of the general field tends to be distributed also among the degrees of freedom in the form of strengths and solenoidal vectors of individual fields. Indeed, these field degrees of freedom are included in the expressions for the field energy as quadratic functions.

In turn, division of the general field into separate fields occurs because new degrees of freedom are released by means of physical analysis, which are characterized by their own fields. We can also say that the 4-potential of the general field can be divided to the 4-potentials of separate fields, and therefore it consists of them. The tendency to distributing the energy of interactions between the fields and substance is a consequence of the energy exchange between the fields and matter particles, and the difference between the fields arises due to different types of interaction.

As it is shown in [14], the gravitational 4-potential of an arbitrary small particle can be presented as the product of the particle’s 4-velocity and the gravitational potential of this particle in its rest system, divided by the square of the speed of light. In this case, the gravitational field of a system of moving particles can be precisely calculated taking into account the superposition principle of potentials and field strengths of a multitude of particles, taking into account the propagation delay of the gravitational effect by using the method of retarded potentials and Lorentz transformations. Although the vector potential of a single particle can be considered proportional to the scalar potential, it is not so for a system of particles, which is the consequence of different rules of summation of scalars and vectors. The scalar and vector potentials of a system of particles become independent of each other.

Exactly the same applies to the electromagnetic field of a system of charged particles. The acceleration field, pressure field and dissipation field were introduced by multiplying the 4-velocity of an arbitrary system’s particle by the potential of the corresponding field at the location of the particle, divided by the square of the speed of light [15]. This approach is suitable for describing the strong interaction field and weak interaction field. In this case the scalar potentials of these fields are proportional to the density of the energy, accumulated by the matter during the reactions of strong and weak interactions per unit mass of the matter.

This is why the 4-potential of the general field  is the sum of the 4-potentials of constituent fields and at the same time it can characterize the interaction of all the fields with the matter. This interaction is described by the product  in the action function (1), while  denotes the mass 4-current.

In [16], gravitation is seen as a consequence of the pressure gradient of the quantum vacuum, which occupies the entire space within and between the bodies. In this static picture for the emergence of gravitation gravitons are not required.

From the classical point of view the universal character of the equations of such fundamental fields as electromagnetic and gravitational fields, is most naturally explained in the Fatio-Le Sage’s theory of gravitation. This theory provides a clear physical mechanism of the gravitational force origination [17-18], as a consequence of the influence of ubiquitous fluxes of gravitons in the form of tiny particles like neutrinos or photons on the bodies. This mechanism also allows us to explain the electromagnetic interaction [13], if we assume the presence of tiny charged particles in graviton fluxes. These graviton fluxes penetrate all bodies and perform electromagnetic and gravitational interaction by means of the field even between distant particles. The particles can also exert direct mechanical action on each other, which can be represented by the pressure field. An inevitable consequence of the action of these fields is deceleration of fast particles in the surrounding medium, which is described by the dissipation field. Finally, the acceleration field is introduced for kinematical description of the motion of particles, the forces acting on them, the energy and momentum. As a result, the general field can be represented as a field, in which neutral and charged particles in the fluxes of neutral and charged gravitons exchange energy and momentum with each other and with gravitons. The energy and momentum of the general field can be associated with the energy and momentum, acquired by the fluxes of gravitons during interaction with the matter; and in order to take into account the system’s energy and momentum we need to add the matter’s energy and momentum from its interaction with gravitons.

We should add to the above-mentioned, that the strong interaction in our opinion can be reduced to strong gravitation, acting at the level of atoms and elementary particles [13], [19-20], with replacement of the gravitational constant by the strong gravitational constant. As for the weak interaction, from the standpoint of the theory of infinite nesting of matter, it is reduced to the processes of matter transformation under the action of fundamental fields, taking into account the action of strong gravitation. Similarly, the pressure field and dissipation field could be reduced to fundamental fields, if we would know all the details of interatomic and intermolecular interactions. Due to the difficulties with such detailed information, we assume the existence of own 4-potentials in the pressure field, energy dissipation field, strong interaction field and weak interaction field, and approximate the action of these fields in the matter using these 4-potentials.

On the other hand, Abdus Salam, Sheldon Glashow and Steven Weinberg have combined with one formalism the weak and electromagnetic interactions in the quantum field theory. This implies that such combination is also possible in the classical description of fields and their action in massive bodies, and we make it based on the same procedure that was used in [5-6], [15]. As for the reactions of strong and weak interactions, we should take into account that they change the energy of massive objects in the macroscopic gravitational and electromagnetic fields. These reactions take place due to emission or absorption of the energy of strong microscopic fields, acting on the atomic level, lead to thermonuclear reactions and are the main source of stellar radiation.

The existence of additional thermonuclear energy sources inside the stars shifts significantly the standard spatial distribution of physical quantities. For example, the estimate of the temperature in the center of the Sun in [7] in general corresponds to the formula of temperature decrease proportionally to the square of the radius, as it follows from the wave equation for the potential of the acceleration field. However, the pressure in the center of the Sun is 58 times less than in the standard Sun model. This deviation occurred because we did not take into account the pressure effect from the energy and momentum acquired by the particles in nuclear reactions due to strong and weak interactions.

If we assume that each of the seven fields under consideration is a special manifestation of the general field, then in case of equilibrium and steady distribution of parameters for the fields of strong and weak interactions we can expect the field equations, similar in the form to the equations for other fields. These equations can be obtained from (7-8) and from equations (A1-A11) in Appendix, with replacement of the potentials and strengths of the general field by similar quantities from Table 2 for the strong interaction field and weak interaction field, respectively. In this case the coefficient  in (6), in formulas (A4) and further on must be replaced by other constant coefficients to be determined for each field. In particular, for the scalar potential of the strong interaction field in the framework of the special theory of relativity we expect the wave equation similar to equation (A10):

 

,                                              (28)

 

where  is a certain coefficient.

 

In stationary case, the potential does not depend on time, and the solution, that follows from (28), is similar to the solution for the pressure field in [7] for a spherical massive body:

 

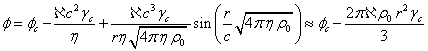,                 (29)

 

where  is the scalar potential of the strong interaction field in the center of the body,  is the Lorentz factor for the particles in the center,  is the coefficient of the acceleration field.

 

We can express the scalar potential by a formula , where  denotes the volume energy density or the pressure, arising from reactions in the matter including strong interaction. Nuclear reactions occur mainly in the stellar core, on the core surface the rate of reactions is low, and at  we can assume that . Then, from (29) we can estimate  in the center of the stellar core:

 

.

 

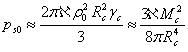Assuming for simplicity that the solar energy is produced mainly in reactions involving strong interaction, equating  to the pressure in the center of the Sun equal to Pa in the standard model [21], and substituting the core mass  equal to 0.34 Solar masses and the core radius  equal to 0.2 Solar radii, we obtain the estimate of the constant: m3/(kg·s2). For comparison, in the formula for the scalar potential of the pressure field, the same as in (29), a similar coefficient in the absence of the strong interaction field equals m3/(kg·s2). According to [7], for the acceleration field the corresponding coefficient also equals , where  is the gravitational constant.

 

References

1.    Georgi, H. and Glashow, S.L. (1974) Unity of All Elementary Particle Forces. Physical Review Letters, 32, 438-441.

2.    Carlip, S. (2001) Quantum Gravity: a Progress Report. Reports on Progress in Physics, 64, 885-942. doi:10.1088/0034-4885/64/8/301.

3.    Kaluza, T. (1921) Zum Unitätsproblem in der Physik. Sitzungsber. Preuss. Akad. Wiss. Berlin. (Math. Phys.): 966–972.

4.    Klein, O. (1926) Quantentheorie und fünfdimensionale Relativitätstheorie. Zeitschrift für Physik  A, 37, 895-906.

5.    Fedosin, S.G. (2016) About the cosmological constant, acceleration field, pressure field and energy. Accepted by Jordan Journal of Physics. http://vixra.org/abs/1403.0023.

6.    Fedosin, S.G. (2015) Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics, 18, 13-24. doi:10.5541/ijot.5000034003.

7.    Fedosin, S.G. (2014) The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics, 3, 152-167. doi:10.11648/j.ajmp.20140304.12.

8.    Fedosin, S.G. (2015) Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics, 8, 1-16.

9.    Fedosin, S.G. (2012) The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, 35, 35-70.

10.              Fedosin, S.G. (2012) The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, 5, 55-75. doi:10.3968%2Fj.ans.1715787020120504.2023.

11.              Науменко Ю. В. (2006) Единая теория векторных полей (от электродинамики Максвелла к единой теории поля). Армавирское полиграф-предприятие, Армавир. http://www.etvp.narod.ru/.

12.              Heaviside, O. (1893) A Gravitational and Electromagnetic Analogy, Part I. The Electrician, 31, 281-282.

13.              Fedosin, S. (2015) The physical theories and infinite hierarchical nesting of matter, Vol. 2. LAP LAMBERT Academic Publishing, Saarbrücken.

14.              Fedosin, S.G. (2013) 4/3 Problem for the Gravitational Field. Advances in Physics Theories and Applications, 23, 19-25.

15.              Fedosin, S.G. (2014) The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, 8, 771-779. doi:10.12988/astp.2014.47101.

16.              Caligiuri, L.M. and Sorli A. (2014) Gravity Originates from Variable Energy Density of Quantum Vacuum. American Journal of Modern Physics, 3, 118-128. doi:10.11648/j.ajmp.20140303.11.

17.              Fedosin, S.G. (2009) Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, 4, 1-24.

18.              Michelini, M. (2007) A flux of Micro-quanta explains Relativistic Mechanics and the Gravitational Interaction. Apeiron Journal, 14, 65-94.

19.              Fedosin, S. G. (1999) Fizika i filosofiia podobiia ot preonov do metagalaktik. Style-Mg, Perm.

20.              Fedosin, S.G. (2012) The radius of the proton in the self-consistent model. Hadronic Journal, 35, 349-363.

21.              Christensen-Dalsgaard et al. (1996) The current state of solar modeling. Science, 272, 1286-1292. doi:10.1126/science.272.5266.1286.

 

Appendix. The characteristics of the general field

The antisymmetric tensor components of the general field are obtained from relation (3). Let us introduce the following notations:

 

,                 ,                    (A1)

 

where the indices  form triplets of non-recurrent numbers of the form 1,2,3, or 3,1,2, or 2,3,1; the 3-vectors  and  can be written by components: ;   .

 

Using these notations the tensor  can be represented as follows:

 

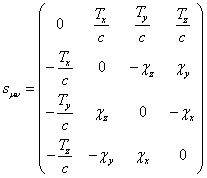.                                                   (A2)

 

 

 

 

The same tensor with contravariant indices equals: . In Minkowski space the metric tensor does not depend on the coordinates, and in this case for the general tensor field we have the following:

 

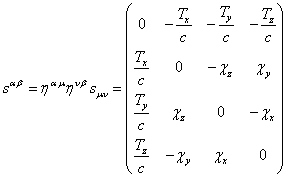.                                       (A3)

 

 

 

 

The general field equation (7) can be expressed in Minkowski space in terms of the vectors  and  using the 4-vector of mass current: , where . Substituting in (7) the covariant derivatives  with the partial derivatives , we find:

 

,     ,     ,     .        (A4)

 

If we multiply scalarly the second equation in (A4) by , and multiply scalarly the fourth equation by  and sum up the results, we will obtain the following:

 

.                            (A5)

 

Equation (A5) contains the Poynting theorem applied to the general field, it is written in a covariant form as the time component of equation (17):

 

.

 

If we substitute (A2) in (17), we can obtain one scalar and one vector relation:

 

,                .                  (A6)

 

The first relation in (A6) is the time component of the motion equation (16) and the second relation is the space component of (16).

The vector  has the dimension of an ordinary 3-acceleration, and the dimension of the vector  is the same as that of the frequency.

Let us substitute the 4-potential of the general field  in the definition (A1):

 

,                           .                                  (A7)

 

The vector  is the general field strength and it is expressed in terms of scalar and vector potentials of the seven fields. The vector  is the solenoidal vector of the general field, depending on the vector potentials of fields.

We can substitute the tensors (A2) and (A3) in (6) and express the stress-energy tensor of the general field  in terms of the vectors  and . Let us write here the expressions for the tensor invariant  and the time components of the tensor :

 

,         ,        .       (A8)

 

The component  defines the energy density of the general field in the given volume, and the vector  defines the energy flux density of the general field.

If we substitute  from (A7) in the first equation in (A4), and take into account the gauge of the 4-potential (14) as follows:

 

,                                              (A9)

 

we will obtain the wave equation for the scalar potential:

 

.                                           (A10)

 

From (A7), (A9) and the second equation in (A4) the wave equation follows for the vector potential of the general field:

 

.                                          (A11)

 

Let us now substitute in (A7) the general field potentials  and , expressed in terms of the potentials of the seven fields, according to (14), provided :

 

 

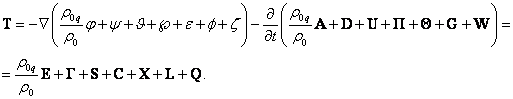
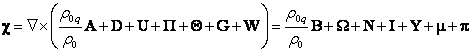.                                (A12)

 

In (A12) we used definitions of the field strengths, such as ,  for the electromagnetic field, and similar definitions for other fields. According to (A12), the strength  and the solenoidal vector  of the general field are expressed in terms of the sums of the corresponding strengths and solenoidal vectors of the seven fields.

If we substitute (A12) in (A2), we will obtain the relation, which coincides with (4) for the general field tensor:

 

.

 

The vectors  and  in (A12) are represented as the sums of the corresponding vectors of the seven fields. Therefore, after substituting (A12) in the general field equations (A4), these equations could be divided into seven sets with four equations in each set, separately for each field. As a result, we could assume that the fields and the equations for these fields are relatively independent of each other. But in general case, such division of the general field equations to separate equations for each field is not always possible. Probably division of equations and independence of fields can take place when energy and momenta distribution between all the fields is completed in the system.

As we can see from (A8), the stress-energy tensor of the general field  includes the vectors products of the vectors  and , as well as the squares of these vectors. If we take into account (A12), then we can see that in the tensor  cross terms appear, containing the products of strengths and solenoidal vectors of all the seven fields. This means that the fields tend to interact with each other, introducing additional cross terms into the energy and momentum of the general field. This does not apply to the force action of the fields on the matter, since there are no cross terms in the equation of motion, according to (16) and (A6).

Source: http://sergf.ru/koen.htm

Scientific site