УДК
523; 524.3
О квантовании и дискретности некоторых параметров у планет и звёзд
С. Г.
Федосин*, А. С. Ким
Пермский
государственный университет, г. Пермь, Россия
* Email
: intelli@list.ru
Показано, что удельные орбитальные механические моменты вращения планет
Солнечной системы могут быть описаны с помощью квантовой формулы Бора для атома
водорода. Выведена соответствующая
квантовая формула и для спина планет. Приведены оценки экстремальных значений
масс и размеров планет, белых карликов и
нейтронных звёзд. Открываемые в последнее время в большом количестве
L-карлики хорошо описываются моделями водородных белых карликов и являются звёздами минимальной массы. Как
следствие делается вывод о том, что квантование и дискретность свойств всех космических объектов, включая и такие малые, как
элементарные частицы, вытекают из их сложной структуры и зависят от степени
вырождения составляющего их вещества.
Понятия
квантования и дискретности достаточно редко применяются в отношении массивных
космических объектов, тогда как современная физика микромира, квантовая
механика, целиком основана на этих понятиях. Тем более интересным оказывается
то, что некоторые результаты квантовой механики можно перенести и на планеты и
звёзды, учитывая свойства подобия атомных и звёздных систем. В каждой из этих
систем можно найти массивный центральный объект, окружённый спутниками - атомное ядро и электроны, звезда и её
планеты. Если найти отношения массы ядра атома к массе электрона, среднего
радиуса орбиты электрона к размеру ядра и энергии ядра к энергии электрона в
атоме, то можно показать, что существуют соответствующие звёздные системы, в
которых выполняются такие же отношения. В результате между всеми атомными и
звёздными системами можно установить однозначные соотношения подобия. Это позволяет,
в частности, применить простейшую квантовую формулу Бора к планетам Солнечной
системы и оценить дискретность их параметров.
Для
объяснения свойств квантования и дискретности,
присущих объектам различной природы, мы используем универсальный энергетический
подход. Исследуются экстремальные значения параметров планет и звёзд и
определяются области существования этих объектов. Анализ результатов
показывает, что равновесные состояния объектов полностью определяются их
внутренней структурой, составом и количеством вещества. Чем более точно
вещество объектов подчиняется квантовым законам, тем более вероятны
дискретность параметров и состояний этих объектов и квантованность при их
взаимодействиях друг с другом.
Характеристики вращения планет
Рассмотрим
орбитальные вращения планет в Солнечной системе с точки зрения квантовой теории
Бора. Сама возможность такого подхода диктуется тем, что график зависимости
орбитальных радиусов от номера планеты ![]() оказывается весьма
гладкой кривой, как и зависимость состояний электрона в атоме водорода. Лишь
Юпитер вследствие своей большой массы несколько выпадает из общей зависимости.
По формуле Бора для атома водорода орбитальный момент электрона квантуется и
равен:
оказывается весьма
гладкой кривой, как и зависимость состояний электрона в атоме водорода. Лишь
Юпитер вследствие своей большой массы несколько выпадает из общей зависимости.
По формуле Бора для атома водорода орбитальный момент электрона квантуется и
равен: ![]() , где
, где ![]() – целое число,
– целое число, ![]() – постоянная Планка.
Для того, чтобы исключить влияние большого разброса
масс у планет, используем эту формулу для расчёта не целых, а удельных
орбитальных моментов планет:
– постоянная Планка.
Для того, чтобы исключить влияние большого разброса
масс у планет, используем эту формулу для расчёта не целых, а удельных
орбитальных моментов планет:
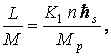 (1)
(1)
где
![]() – орбитальный момент,
масса и номер планеты соответственно,
– орбитальный момент,
масса и номер планеты соответственно,
![]() = 0,5 – коэффициент пропорциональности,
= 0,5 – коэффициент пропорциональности,
![]() Дж·с
– характерный момент импульса для звёздных систем,
Дж·с
– характерный момент импульса для звёздных систем,
![]() кг – масса планеты-аналога электрона.
кг – масса планеты-аналога электрона.
Величины ![]() определены с помощью
теории подобия в [1]. Заметим, что спин Солнца согласно [2] равен
определены с помощью
теории подобия в [1]. Заметим, что спин Солнца согласно [2] равен ![]() Дж·с и близок к величине
Дж·с и близок к величине ![]() .
.
Точность
соотношения (1) не хуже 25 %. Поскольку планеты слабо взаимодействуют друг с
другом, Солнечная система по (1) аналогична атому водорода с тем отличием, что
вместо одной имеется девять планет, расположенных на эквивалентных боровских
орбитах. Хотя атомы и планетные системы звёзд являются разными объектами,
дискретность орбит планет с неизбежностью вытекает из теории возникновения
Солнечной системы при учёте гравитационных волн плотности вещества в
допланетном диске, распределения в нём температуры и других факторов.
Можно
предположить, что в Солнечной системе квантуются и спины планет. Введём понятия
характерного момента импульса ![]() и характерной
скорости
и характерной
скорости ![]() для любого объекта:
для любого объекта:
![]() ,
,
здесь
![]() – масса,
– масса, ![]() – радиус объекта,
– радиус объекта, ![]() определяется через
энергию связи объекта
определяется через
энергию связи объекта ![]() :
: ![]() .
.
Для планет энергия связи равна половине гравитационной
энергии:
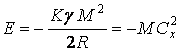 . Тогда
. Тогда  ,
,
где
![]() – коэффициент порядка 1,
– коэффициент порядка 1, ![]() для однородного шара,
для однородного шара,
![]() – гравитационная постоянная.
– гравитационная постоянная.
Спин
электрона обычно определяют через постоянную Планка
как характерный момент импульса: ![]() . Аналогично для планет считаем, что спин
. Аналогично для планет считаем, что спин ![]() пропорционален
пропорционален ![]() . Учитывая определения
. Учитывая определения ![]() и
и ![]() , находим:
, находим:
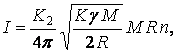 (2)
(2)
где ![]() = 0,25 – коэффициент
пропорциональности, а спин планеты
= 0,25 – коэффициент
пропорциональности, а спин планеты ![]() пропорционален номеру
планеты
пропорционален номеру
планеты ![]() .
.
Соотношение
(2) неплохо выполняется для большинства планет, за исключением Меркурия
(заторможен Солнцем) и Венеры, слабое обратное вращение которой, по-видимому,
было вызвано какими-то сильными столкновениями.
Большие
и малые планеты
Квантование
масс и энергий атомов и элементарных частиц обнаружено довольно давно. Так как
при переходе из одного состояния в другое квантовая система изменяет свою массу
и энергию порциями или квантами, то это означает, что сами состояния являются
выделенными какими-то законами природы. Для планет и звёзд также имеются
выделенные состояния. Покажем, например, что при рождении планетной системы
образование планет с массой более массы Юпитера становится маловероятным. Мы
можем считать, что образующиеся большие планеты состоят в основном из водорода.
Пока масса мала, гравитационная энергия планеты и её тепловая (внутренняя
кинетическая) энергия в расчёте на один нуклон не превышают энергии электрона в
атоме водорода. И наоборот, если масса планеты велика, электронные оболочки
атомов будут сминаться под действием высокого давления в её недрах, а электроны
начинают вырождаться как в белых карликах (БК). Поэтому для самых массивных
планет в качестве граничного условия можно записать равенство модулей
гравитационной энергии и суммарной электростатической энергии электронов во всех атомах водорода:
 , (3)
, (3)
где 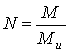 – число нуклонов,
– число нуклонов,
![]() – масса нуклона,
– масса нуклона,
![]() – электрический заряд,
– электрический заряд,
![]() – электрическая
постоянная,
– электрическая
постоянная,
![]() м
– радиус Бора.
м
– радиус Бора.
Учитывая
равенство объёмов планеты, выраженных через радиус планеты ![]() и через суммарный
объём атомов водорода, составляющих вещество планеты:
и через суммарный
объём атомов водорода, составляющих вещество планеты: ![]() , при
, при ![]() = 0,6 из (3) находим
массу и радиус массивной планеты:
= 0,6 из (3) находим
массу и радиус массивной планеты:
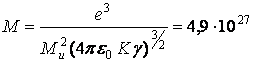 кг
кг ![]() (4)
(4)
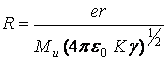 =
= ![]() м
м
![]() (5)
(5)
где
![]() - масса и радиус Юпитера.
- масса и радиус Юпитера.
Видно,
что Юпитер по своим параметрам действительно близок к планете с предельной массой.
Для
оценки параметров самых малых планет с учётом теоремы вириала приравняем
половину гравитационной энергии планеты к её внутренней тепловой энергии:
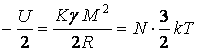 , (6)
, (6)
где
![]() - постоянная
Больцмана,
- постоянная
Больцмана,
![]() - средняя температура планеты,
- средняя температура планеты,
![]() -
масса планеты, выраженная через плотность её вещества
-
масса планеты, выраженная через плотность её вещества ![]()
и радиус ![]() .
.
Используя
равенство 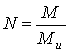 , из (6) можно выразить массу и радиус:
, из (6) можно выразить массу и радиус:
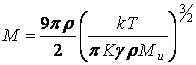 , (7)
, (7)
 .
(8)
.
(8)
Подставляя
в (7), (8) плотность вещества такую же, как у малой планеты - крупнейшего из астероидов Цереры (![]() = 2,1×103
кг/м3 согласно [3] ), а в качестве наименьшей температуры тела в
космическом пространстве используя величину
T = 2,7 К
(температура фонового излучения), найдём параметры малой планеты, в которой
гравитационные силы ещё способны формировать шарообразную форму: M = 7,3×1020
кг, R = 440 км. Для сравнения приведём массу и
радиус Цереры - 1,2×1021 кг и 512 км
соответственно.
= 2,1×103
кг/м3 согласно [3] ), а в качестве наименьшей температуры тела в
космическом пространстве используя величину
T = 2,7 К
(температура фонового излучения), найдём параметры малой планеты, в которой
гравитационные силы ещё способны формировать шарообразную форму: M = 7,3×1020
кг, R = 440 км. Для сравнения приведём массу и
радиус Цереры - 1,2×1021 кг и 512 км
соответственно.
Экстремальные значения параметров белых карликов и нейтронных звёзд
Имеется
немало точных расчётов параметров БК и нейтронных звёзд с интегрированием возможных
уравнений равновесия вещества и учётом различных эффектов. Метод сравнения
энергий и в этом случае позволяет обойтись без интегрирования и даёт достаточно
точные результаты. Давление в недрах БК и нейтронных звёзд поддерживается
вырожденными электронами и нейтронами соответственно. Размер кубической ячейки,
в которой находятся вырожденные частицы, равен:
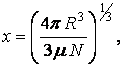 (9)
(9)
здесь
![]() – число вырожденных частиц на один нуклон.
Соотношение (9) получается путём деления сферического объёма планеты на число
нуклонов N и величину
– число вырожденных частиц на один нуклон.
Соотношение (9) получается путём деления сферического объёма планеты на число
нуклонов N и величину ![]() . Рассматривая движение частиц в ячейке как движение в потенциальной яме, с
помощью квантовой механики аналогично [4] можно оценить их минимальную энергию
в расчете на один нуклон:
. Рассматривая движение частиц в ячейке как движение в потенциальной яме, с
помощью квантовой механики аналогично [4] можно оценить их минимальную энергию
в расчете на один нуклон:
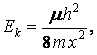 (10)
(10)
где ![]() – масса вырожденной
частицы.
– масса вырожденной
частицы.
В
соответствии с теоремой вириала можно считать, что половина модуля
гравитационной энергии звезды ![]() равна кинетической
энергии движения вырожденных частиц, то есть:
равна кинетической
энергии движения вырожденных частиц, то есть:
 .
.
С учётом
(9) и соотношения
![]() получаем:
получаем:
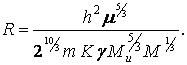 (11)
(11)
Приведём
(11) к стандартному виду, введя ![]() =
= ![]() как число нуклонов на
одну вырожденную частицу, и отсчитывая массу звезды
как число нуклонов на
одну вырожденную частицу, и отсчитывая массу звезды ![]() в единицах массы
Солнца
в единицах массы
Солнца ![]() . Для БК
. Для БК ![]() в (11) равна массе
электрона, а радиус будет равен:
в (11) равна массе
электрона, а радиус будет равен:
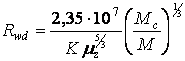 м. (12)
м. (12)
У
водородного БК ![]() = 1, у гелиевых и углеродных БК
= 1, у гелиевых и углеродных БК ![]() можно принять равным
2.
можно принять равным
2.
Для
нейтронной звезды ![]() в (11)
будет массой нуклона, а
в (11)
будет массой нуклона, а ![]() = 1
:
= 1
:
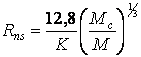 км.
км.
Водородный БК не может быть массивнее,
чем 0,07 – 0,08 ![]() , поскольку водород
загорится в термоядерной реакции и возникнет звезда главной последовательности
(звезда ГП). Соответствующий верхний предел массы для гелиевых БК согласно [5]
составляет не менее 0,31
, поскольку водород
загорится в термоядерной реакции и возникнет звезда главной последовательности
(звезда ГП). Соответствующий верхний предел массы для гелиевых БК согласно [5]
составляет не менее 0,31 ![]() .
.
На
рисунке представлена зависимость радиуса от массы для больших планет и звёзд
ГП. Большой точкой обозначена планета с наибольшими
массой и радиусом по соотношениям (4), (5). Короткая линия для водородных БК построена
по соотношению (12) при ![]() = 1 , её пересечение с общей зависимостью для планет и звёзд
ГП отмечено значком
= 1 , её пересечение с общей зависимостью для планет и звёзд
ГП отмечено значком ![]() , с другой стороны эта линия ограничена значением массы 0,08
, с другой стороны эта линия ограничена значением массы 0,08 ![]() . Величина массы
. Величина массы ![]() имеет значение порядка
0,056
имеет значение порядка
0,056![]() и может считаться
минимальной массой наблюдаемых звёзд. Только в последнее время благодаря
улучшенной технике инфракрасных измерений было обнаружено большое количество
таких звёзд с характерной массой 0,06
и может считаться
минимальной массой наблюдаемых звёзд. Только в последнее время благодаря
улучшенной технике инфракрасных измерений было обнаружено большое количество
таких звёзд с характерной массой 0,06![]() и температурой 1500 -
2000 К, названных L-карликами.
и температурой 1500 -
2000 К, названных L-карликами.
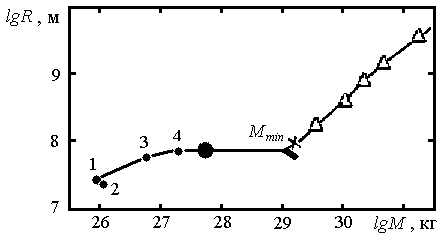
Обозначения: 1 –
Уран, 2 – Нептун, 3 –
Сатурн, 4 –
Юпитер, l – планета с предельной массой, ![]() – минимальная масса БК, r –
звезда ГП с массой
– минимальная масса БК, r –
звезда ГП с массой ![]() ê –
звёзды ГП.
ê –
звёзды ГП.
Предел
Чандрасекхара для параметров вырожденной звезды с
ультрарелятивистскими частицами получается, если (10) сравнивать с энергией
покоя носителей:
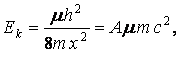 (13)
(13)
а
также считать, что полная энергия звезды равна нулю:
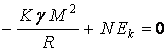 ,
(14)
,
(14)
здесь
![]() – коэффициент,
задающий долю гравитационной энергии по отношению к энергии покоя. Комбинируя
далее (9), (13), (14) с учётом выражений:
– коэффициент,
задающий долю гравитационной энергии по отношению к энергии покоя. Комбинируя
далее (9), (13), (14) с учётом выражений:
![]() ,
, ![]() , находим массу и радиус:
, находим массу и радиус:
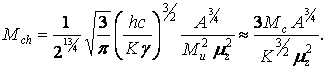 (15)
(15)
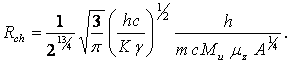 (16)
(16)
Величина ![]() не зависит от
массы
не зависит от
массы ![]() вырожденных частиц.
Для неводородных БК используя вместо
вырожденных частиц.
Для неводородных БК используя вместо ![]() массу электрона и при
массу электрона и при ![]() ,
, ![]()
![]() получается:
получается:
![]() ,
, ![]() м.
м.
Величину
![]() для массивных
нейтронных звёзд можно оценить с помощью результатов из [1], где исследовалось
равновесие чёрного тела из нуклонов и электромагнитного поля с учётом энергии
нулевых колебаний и временной устойчивости нуклонов. Для энергии колебаний
найдено пороговое значение
для массивных
нейтронных звёзд можно оценить с помощью результатов из [1], где исследовалось
равновесие чёрного тела из нуклонов и электромагнитного поля с учётом энергии
нулевых колебаний и временной устойчивости нуклонов. Для энергии колебаний
найдено пороговое значение ![]() , так что принимая в (13)
, так что принимая в (13) ![]() = 1/6, при
= 1/6, при ![]() ,
, ![]() ,
, ![]() из (15), (16) находим:
из (15), (16) находим: ![]() ,
, ![]() км. Таким образом,
масса нейтронной звезды не может превысить величину
км. Таким образом,
масса нейтронной звезды не может превысить величину ![]() , а радиус звезды должен быть больше, чем
, а радиус звезды должен быть больше, чем ![]() .
.
Заключение
Представленная
цепь рассуждений однозначно приводит нас к следующему выводу: области
существования составных космических объектов типа планет и звёзд целиком
обусловлены наличием квантованных состояний взаимодействующих частиц, то есть
атомов, нуклонов, электронов, фотонов и т.д. По-видимому, та или иная степень
квантования свойств и дискретности состояний характерна для всех устойчивых и
долгоживущих систем. Как для планет дискретность момента импульса возникает
вследствие эволюции протопланетного вещества вблизи звезды, так и состояния
самих звёзд определяются эволюцией их собственного вещества. При этом, чем больше уровень вырождения частиц, чем больше плотность
вещества, тем более вероятно сужение области существования составных объектов
вплоть до дискретных состояний. Так, массы большинства изученных нейтронных
звёзд лежат вблизи значения 1,4 ![]() [3]. Это можно объяснить тем, что в предсверхновой коллапс ядра
звезды начинается при вполне определённой массе ядра и мало зависит от
массы оболочки. Приблизительно такая же масса получается и из (15) для предельной
массы БК при
[3]. Это можно объяснить тем, что в предсверхновой коллапс ядра
звезды начинается при вполне определённой массе ядра и мало зависит от
массы оболочки. Приблизительно такая же масса получается и из (15) для предельной
массы БК при ![]() = 2 , причём ядра предсверхновых близки по своим свойствам к
БК.
= 2 , причём ядра предсверхновых близки по своим свойствам к
БК.
Переходя
теперь к элементарным частицам, можно заключить по методу индукции и теории
подобия, что квантованность и дискретность их состояний также возникает
благодаря сложной внутренней структуре, как следствие многокомпонентности
внутреннего состава самих частиц и вырождения их вещества.
Л и т е р а т у р а
1. Федосин С. Г. Физика и философия подобия
от преонов до метагалактик. - г. Пермь: Стиль-МГ, 1999. -544 с.
2. Аллен
К. У. Астрофизические величины. - М.: Мир, 1977.- 446 с.
3. Мартынов
Д. Я. Курс общей астрофизики. - М.: Гл. ред. физ.-мат. лит., 1988.-640 с.
4. Ахиезер
А. И. Атомная физика. Справочное пособие. - Киев: Наукова
думка, 1988. - 267 с.
5. Kox J., Salpeter E. E. Equilibrium
models for helium-burning star. III. Semi-degenerate stars of small mass //
Astrophys. J. 1964. V. 140. P. 485 -
498.
About quantization and
discreteness of some parameters in planets and stars
S. G. Fedosin, A. S. Kim
Perm State University, Perm, Russia
We
show that specific orbital mechanical rotational moments of planets in Sun
system may be described with the help of Bohr quantum formula for hydrogen
atom. We derive corresponding quantum formula for spin of planets too. The
extreme quantities of mass and radius were evaluated for planets, white dwarfs
and neutron stars. Models of hydrogen white dwarfs are good for numerous
L-dwarfs, which were opened last time. They have minimum mass among the stars.
As a consequence we conclude that quantization and discreteness of properties of space objects including
infinitely small elementary particles, stream from their composite structure and depend on a degeneracy of
their component substance.
Источник:
http://sergf.ru/qd.htm