На русском языке
Gravitational
model of strong interaction
Gravitational model of strong
interaction is the
model, in which strong interaction is described by strong gravitation, the action of gravitational torsion field and
electromagnetic forces.
Contents
|
Standard theory
In elementary particle physics the generally accepted
model is the Standard model according to which strong interaction occurs on the
scale, not much greater than the size of atomic nuclei. In this case, there are
considered two different possible situations – strong interaction between
nucleons (or between other hadrons), and strong interaction in the matter of
hadrons. In the first case the pion-nucleon Yukawa interaction is often used,
according to which the role of carriers of strong interaction between nucleons
is played by virtual pions and other mesons. In the second case quantum
chromodynamics (QCD) is involved, in which hadrons are composed of quarks,
there are two quarks in each meson, and three quarks in baryons. Quarks
interact by gluons and can not exist outside hadrons
in the free form. Except two or three valence quarks, a hadron must contain
gluon clouds surrounding quarks and seas of virtual particles such as
quark-antiquark and electron-positron pairs, W and Z bosons. In QCD gluons are
considered the carriers of strong interaction, and the interaction between
nucleons is treated as a residual effect of the quark gluon fields that goes
beyond hadrons. As a result, the forces between two nucleons must be much less
than the forces between the quarks inside these nucleons.
At present the description of strong interaction between
nucleons through virtual pions to some extent looks archaic and does not seem
satisfactory. For example, it is unclear at what point between nucleons these
virtual pions should appear, what is the mechanism of their origin and
subsequent action. How can the momentum transfer from virtual pions either
attract nucleons, or repel them depending on the distance between the nucleons?
Due to what does the tensor component of nuclear forces, which is not purely
radial, arise? From a philosophical point of view, reduction of the interaction
between elementary particles to other elementary particles seems rather an
artificial device, than description of the essence of phenomena.
QCD also has its own problems analyzed in the model of quark quasiparticles. Among the
main problems are: introducing into the Standard theory many new unexplained
entities and adjustable parameters; considering interactions as point events
with quarks and bosons of point sizes and subsequent discrepancy in solutions;
unobservability of free quarks and gluons, indicating that they are
quasiparticles; color confinement as retention of color charge in hadrons, and
asymptotic freedom of quarks at short distances between them; different masses
of quarks with equal spins and two fixed values of the fractional elementary
charge; the reason for collapse of massive quarks; specification of
defragmentation method and hadronization of jets with obligatory conversion of
various color quarks into colorless hadrons; the origin of quantum numbers of
quarks, etc.
Gravitational model
Origin of mass
In the Standard model it is assumed that quarks, leptons,
W and Z bosons acquire mass through the
mechanism of spontaneous symmetry breaking and Higgs bosons. After that hadrons
consisting of quarks also become massive. If we proceed from the theory of Infinite Hierarchical Nesting of Matter,
the mass appears as an intrinsic property of material particles that occurs as
a result of Le Sage's theory of gravitation. [1] [2]
At the level of elementary particles strong gravitation influences the
scattered matter, forming objects, containing different amounts of substance.
Further, these objects evolve similarly to the main sequence stars, turning into low-mass particles like
nuons and in nucleons. According to the substantial neutron model, neutrons appear
first, and then protons and electrons emerge as a result of beta decay.
At
the level of stars neutron corresponds to a neutron star, proton corresponds to a magnetar, pions correspond to neutron stars with minimum mass
decaying in time, [3] and nuons correspond to white dwarfs. [4] Discreteness of masses of these objects
is defined by a narrow range of masses, in which formation of these objects is
possible in the field of strong (or, respectively, ordinary) gravitation
according to the equation of their matter state.
The reason of mass and its inertia in the general case is
interaction of gravitons with matter. This interaction leads to attraction of
bodies and to the concept of gravitational mass. At the same time, in case of
acceleration of bodies relative to the fluxes of gravitons inertial mass and
the corresponding inertial force appear. Taking into account the similarity of matter levels and SPФ symmetry, such description of
gravitation is universal for all levels of matter. Meanwhile, in general
relativity, mass is considered as the consequence of curvature of spacetime
around the matter and in elementary particle physics the Higgs mechanism is
introduced to describe the mass. As we can see, in the latter case,
representation of mass is ambiguous and depends strongly on the size and mass
of the objects.
The estimate of the mass and sizes of nucleons can be
obtained in the same way which was used in the study of properties of neutron
stars based on the principles of quantum mechanics. [5]
From comparison of the gravitational binding energy of the star and the quantum
mechanical energy of matter (expressed by Planck constant) we obtain formulas
for the mass and radius of the star. Similar formulas are used for nucleons as
the analogues of neutron stars. It turns out that the mass and radius of
nucleons are determined by quantum properties of their matter and depend on the
value of strong gravitational constant.
For connection of the radius and mass of the proton the following formula is
obtained: [6]
![]()
where ![]() is
a constant depending on the properties of the proton matter.
is
a constant depending on the properties of the proton matter.
Charge
The electromagnetic field, along with gravitational, is
the fundamental force field. Natural objects, containing matter at low density
and low energy of interaction, are generally neutral due to the compensation of
positive and negative charges of the matter. Charged objects occur when the
carriers of charge of a single sign are removed from (or added to) them.
Characteristic and widespread process is acquisition of a positive charge by
the proton and formation of a negatively charged electron in beta decay due to
reactions of weak interaction occurring in the neutron matter. The analysis of
energies in the proton shows that the proton charge has the maximum possible
value when the density of zero electromagnetic energy is comparable to the
energy density of strong gravitation. [6]
Equality of the charge of proton and electron follows from the nature of
neutron beta decay and takes place in every point of the Universe.
Secondary character of mass and charge of the electron in
the hydrogen atom with respect to the proton follows from substantial electron model. In particular,
the electron matter must have the charge equal to the charge of the proton, to
ensure electrical neutrality of the atom. At the same time the mass of the
electron must be of such value that its attraction to the nucleus in the strong
gravitational field must be equal to the electric force between the charges of
the nucleus and the electron. In addition, there are two almost identical
forces: repulsion of the charged matter of the electron cloud from itself, and
the centrifugal force of rotation. The sum of these four forces is zero in
stationary rotation of the electron cloud, which allows determining the strong
gravitational constant. In the process of nucleosynthesis of more massive atoms
from hydrogen atom each time interaction of neutrons, protons and electrons
takes place. It helps to understand the origin of the elementary charge and the
necessity to use it in elementary particle physics and in atomic physics as the
standard unit of charge. Thus, the origin of mass and charges of elementary
particles does not require introduction of hypothetical fields like the Higgs
field.
Energy
Since at the level of elementary particles the main force
is assumed strong gravitation, it
allows us to calculate total energy of hadron of nucleon type, which is up to
sign equal to the binding energy of the hadron matter: [3] [6]
![]()
Here ![]() for
objects like nucleons and neutron stars,
for
objects like nucleons and neutron stars, ![]() is the strong gravitational constant,
is the strong gravitational constant,
![]() and
and ![]() are the mass and radius of the hadron.
are the mass and radius of the hadron.
Relation (1) can be used to estimate approximately the
particle radius by its known mass, rewriting (1) in the form ![]() where
where ![]() and
and ![]() are the mass and radius of the proton. If we substitute the obtained radii
of the particles into (2), we obtain the gravitational binding energies of the
particles shown in the Table. [6]
are the mass and radius of the proton. If we substitute the obtained radii
of the particles into (2), we obtain the gravitational binding energies of the
particles shown in the Table. [6]
|
Characteristics
of proton, pion and muon |
||||
|
Particle |
Mass-energy, MeV |
Mass, 10–27 kg |
Radius, 10–16
m |
Binding energy |
|
Proton p+ |
938.272029 |
1.6726 |
8.7 |
938.272 |
|
Meson |
600 |
1.1 |
10 |
354 |
|
Pion π+ |
139.567 |
0.249 |
16.4 |
11 |
|
Muon μ+ |
105.658 |
0.188 |
10900 |
0.095 |
The particle masses in Table are obtained by dividing the
mass-energy converted from MeV to J, by the squared speed of light. The
mass-energy corresponds to the rest energy in the special relativity, and is
directly proportional to the mass (see the mass–energy equivalence). In
contrast to this, the total energy of the particle is calculated by summing the
potential energy of strong gravitation and the internal kinetic energy of
particle matter, the absolute value of the total energy is equal to the binding
energy or the energy required to scatter the particle matter to infinity with
zero velocity. According to the Table the binding energy of pion matter in the
strong gravitational field is one order of magnitude less than the rest energy,
which is the consequence of low density of the pion matter.
The laws of conservation of energy and momentum in
reactions with elementary particles in the special theory of relativity are as
follows:
![]()
![]()
where before the interaction there are n particles, and
after the interaction the number of particles is m, and there is a possibility
that ![]() ,
, ![]() and
and ![]() are corresponding mass and momentum of particles,
are corresponding mass and momentum of particles, ![]() is
the speed of light.
is
the speed of light.
On the other hand, the energy balance can be written in
such a way as to explicitly include the change in the total energy of
particles: [6]
![]()
where ![]() is the
total energy of the k-th particle in the field of
strong gravitation,
is the
total energy of the k-th particle in the field of
strong gravitation, ![]() is
the radius of the k-th particle,
is
the radius of the k-th particle, ![]() is the kinetic energy of the k-th particle in the special theory of relativity, and during
interaction the energy of strong gravitation
is the kinetic energy of the k-th particle in the special theory of relativity, and during
interaction the energy of strong gravitation ![]() can be released (or, conversely, be added) which is associated with change
in the radii and masses of particles, as well as the energy of the emerging
electromagnetic and neutrino emission
can be released (or, conversely, be added) which is associated with change
in the radii and masses of particles, as well as the energy of the emerging
electromagnetic and neutrino emission ![]() .
.
Structure of nucleons
According to the substantial
neutron model and the substantial
proton model, the difference between neutron and proton besides mass and
charge is mainly in the difference in their internal electromagnetic structure.
Thus, in neutron the space charge separation is assumed, the center of the
neutron is positively charged, and the shell is negative. The rotation of the
space charge creates a negative magnetic moment of neutron, directed opposite
to the spin.
To connect the medium pressure ![]() and the mass density
and the mass density ![]() of
nucleon in the first approximation, we can write down:
of
nucleon in the first approximation, we can write down:
![]()
where ![]() in SI units is the coefficient,
found by the radius of nucleon, its mass and strong gravitational constant. [6] In the self-consistent model that takes into
account the density distribution, the rest energy, magnetic moment and the
conditions of limiting rotation, the ratio of the central proton mass density
to its average density is 1.57. [7]
in SI units is the coefficient,
found by the radius of nucleon, its mass and strong gravitational constant. [6] In the self-consistent model that takes into
account the density distribution, the rest energy, magnetic moment and the
conditions of limiting rotation, the ratio of the central proton mass density
to its average density is 1.57. [7]
From the point of view of the matter state, instead of
three quarks and indefinite number of gluons inside nucleons we expect up to ![]() of
smallest particles called praons.
According to the theory of Infinite Hierarchical Nesting of Matter, praons have the same status in nucleons as
nucleons themselves in neutron stars. This explains why in collisions even with
highest energies we observe not gas of quarks and gluons, but jets of almost
perfect liquid hadronic matter. [8] [9]
of
smallest particles called praons.
According to the theory of Infinite Hierarchical Nesting of Matter, praons have the same status in nucleons as
nucleons themselves in neutron stars. This explains why in collisions even with
highest energies we observe not gas of quarks and gluons, but jets of almost
perfect liquid hadronic matter. [8] [9]
In the above picture de
Broglie wavelength of moving nucleons and other elementary particles can be
explained as a consequence of the relativistic transformation of wavelength of
the internal oscillations of the fundamental fields potentials of the particles
in the laboratory frame of reference.
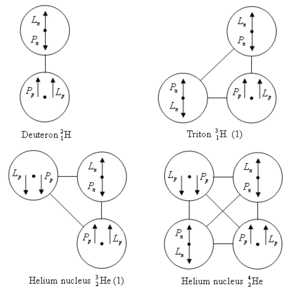
Deuteron
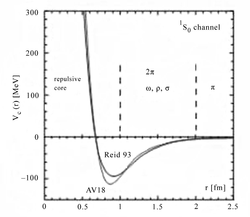
Deuteron is the simplest nucleus consisting of two
nucleons – proton and neutron. In Figure P2 there are two examples of modern
potential of nuclear force depending on distance ![]() , which can be considered equal to the
distance from the center of mass of the system of two nucleons to the center of
one of the nucleons. From internucleon potential, understood as interaction
energy of two nucleons, we can proceed to the force acting on the nucleon,
according to the formula:
, which can be considered equal to the
distance from the center of mass of the system of two nucleons to the center of
one of the nucleons. From internucleon potential, understood as interaction
energy of two nucleons, we can proceed to the force acting on the nucleon,
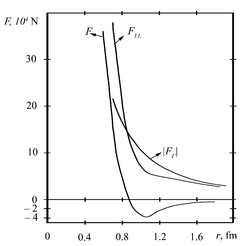
according to the formula: ![]() The graph of this force is shown in
Figure P3 for the potential AV18.
The graph of this force is shown in
Figure P3 for the potential AV18.
In the gravitational model of strong interaction the
force ![]() between nucleons in the first approximation
is presented as the difference between the force of spin repulsion
between nucleons in the first approximation
is presented as the difference between the force of spin repulsion ![]() and the magnitude of gravitational force of attraction
and the magnitude of gravitational force of attraction ![]() : [4]
: [4]
![]()
where ![]() is
the gravitational torsion field from one
nucleon, which acts on the effective spin
is
the gravitational torsion field from one
nucleon, which acts on the effective spin ![]() of
the other nucleon,
of
the other nucleon, ![]() and
and ![]() are the masses of neutron and proton, respectively,
are the masses of neutron and proton, respectively, ![]() is the distance between the centers of
nucleons,
is the distance between the centers of
nucleons, ![]() is
the coefficient, the estimate of which for the case of two nucleons is
is
the coefficient, the estimate of which for the case of two nucleons is ![]() as a result of exponential absorption of
gravitons in the matter of nucleons, and for particles of lower density it is
as a result of exponential absorption of
gravitons in the matter of nucleons, and for particles of lower density it is ![]() .
.
Spin ![]() includes the initial nucleon spin, and the
spin induced by another nucleon by means of gravitational
induction. The formula for the repulsive force of nucleon spins is: [4]
includes the initial nucleon spin, and the
spin induced by another nucleon by means of gravitational
induction. The formula for the repulsive force of nucleon spins is: [4]
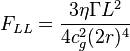 ,
,
where ![]() is
the speed of propagation of gravitational effect (the speed of gravity), which
is close to the speed of light,
is
the speed of propagation of gravitational effect (the speed of gravity), which
is close to the speed of light, ![]() is
the coefficient depending on the distance of nucleons interaction in the
deuteron.
is
the coefficient depending on the distance of nucleons interaction in the
deuteron.
Since in Figure P3 at ![]() fm the force
fm the force ![]() vanishes, we can estimate the distance
between the surfaces of nucleons:
vanishes, we can estimate the distance
between the surfaces of nucleons: ![]() fm. The described state with opposite
nucleon spins has small binding energy of about 69 keV and therefore is
unstable. If we locate nucleons in this state on the plane, the spins of
nucleons will be perpendicular to the plane and opposite to each other.
fm. The described state with opposite
nucleon spins has small binding energy of about 69 keV and therefore is
unstable. If we locate nucleons in this state on the plane, the spins of
nucleons will be perpendicular to the plane and opposite to each other.
From Figure P3 we see that when ![]() , that is in nucleons’ contact, the spin
repulsive force from the torsion field is equal to the gravitational force of
attraction. At smaller distances a rapidly growing force of repulsion emerges.
We can assume that the main contribution is made by the magnetic force of
repulsion and the force of internal pressure in the matter of nucleons.
, that is in nucleons’ contact, the spin
repulsive force from the torsion field is equal to the gravitational force of
attraction. At smaller distances a rapidly growing force of repulsion emerges.
We can assume that the main contribution is made by the magnetic force of
repulsion and the force of internal pressure in the matter of nucleons.
At distances from ![]() m to
m to ![]() m the force from the torsion field decreases according to the
dependence
m the force from the torsion field decreases according to the
dependence ![]() , where
, where ![]() .
If the nucleons (neutron and proton), considered as points were
interacting only by torsion fields from their constant spins, the dependence on
the distance in the formula for the force of spin interaction would have the
form
.
If the nucleons (neutron and proton), considered as points were
interacting only by torsion fields from their constant spins, the dependence on
the distance in the formula for the force of spin interaction would have the
form ![]() .
However, when two nucleons approach each other in deuteron formation,
additional effects can occur. Firstly, in case of the same direction of spins,
due to the effect of gravitational induction both nucleons will rotate each
other as they approach, with increasing of their spins. Secondly, besides
gravitational forces there are also electromagnetic ones, which are the forces
of repulsion of magnetic moments in deuteron (and the magnitude of magnetic
moments due to various effects can also change as the nucleons approach each
other). All this leads to the fact that in the effective force
.
However, when two nucleons approach each other in deuteron formation,
additional effects can occur. Firstly, in case of the same direction of spins,
due to the effect of gravitational induction both nucleons will rotate each
other as they approach, with increasing of their spins. Secondly, besides
gravitational forces there are also electromagnetic ones, which are the forces
of repulsion of magnetic moments in deuteron (and the magnitude of magnetic
moments due to various effects can also change as the nucleons approach each
other). All this leads to the fact that in the effective force ![]() of
nucleons repulsion the exponent increases up to the values greater than
of
nucleons repulsion the exponent increases up to the values greater than ![]() . Thus, from a qualitative point of view,
the gravitational forces of attraction and the forces of spins interaction and
the electromagnetic forces can explain the nuclear forces at short distances.
. Thus, from a qualitative point of view,
the gravitational forces of attraction and the forces of spins interaction and
the electromagnetic forces can explain the nuclear forces at short distances.
At distances greater than ![]() m the force
m the force ![]() in Figure P3, built as the sum of the force
in Figure P3, built as the sum of the force ![]() from internucleon potential and the magnitude of the gravitational force
from internucleon potential and the magnitude of the gravitational force ![]() , undergoes a strange kink, with a
significant change in the speed of its decrease with distance. This is due to
the inaccuracy of internucleon potential of the Standard model, according to
which the interaction between nucleons occurs by means of special carriers –
virtual mesons (in Figure P2 the areas are indicated where interactions with
two pions 2π, with mesons ρ, ω, σ, and one meson π are taken into account) .
Until now, the basis for calculation of the potential at these distances is the
Yukawa potential of the following form:
, undergoes a strange kink, with a
significant change in the speed of its decrease with distance. This is due to
the inaccuracy of internucleon potential of the Standard model, according to
which the interaction between nucleons occurs by means of special carriers –
virtual mesons (in Figure P2 the areas are indicated where interactions with
two pions 2π, with mesons ρ, ω, σ, and one meson π are taken into account) .
Until now, the basis for calculation of the potential at these distances is the
Yukawa potential of the following form:
![]()
where ![]() is
some effective charge of strong interaction,
is
some effective charge of strong interaction, ![]() is the mass of the particle – the carrier of interaction,
is the mass of the particle – the carrier of interaction, ![]() is the Dirac constant.
is the Dirac constant.
For the pion the quantity ![]() in the exponent is equal to one
with
in the exponent is equal to one
with ![]() m, with masses of heavier mesons the distance decreases. The force from the
Yukawa potential, which has the character of attraction, equals:
m, with masses of heavier mesons the distance decreases. The force from the
Yukawa potential, which has the character of attraction, equals:
![]()
At such distances ![]() , where
, where ![]() , the force
, the force ![]() decreases slowly enough, in proportion
decreases slowly enough, in proportion ![]() .
This creates a kink in Figure P3 for the force of spins interaction
.
This creates a kink in Figure P3 for the force of spins interaction ![]() . At the same time, the gravitational
force
. At the same time, the gravitational
force ![]() changes in proportion
changes in proportion ![]() , that is, faster than the force
, that is, faster than the force ![]() from the Yukawa potential at the segment
from the Yukawa potential at the segment ![]() m.
m.
If we proceed from the gravitational and electromagnetic
interactions, the formula for the total energy of interaction between nucleons
in the deuteron must include gravitational energy, the energy of spins and
spin-orbital gravitational interactions, the energy of spin-spin and
spin-orbital interaction of the magnetic moments taking into account the
possible effect of electromagnetic induction, increment of kinetic and
rotational energy of nucleons, which may depend on the distance between the
nucleons, due to the interaction of the gravitational and electromagnetic
forces. Almost all of these energies can contribute to the creation of the
effective force between nucleons.
In the deuteron we can assume that the nucleons are on
the common axis of rotation, and the nucleon spins are directed in one side of
the axis. Then, the magnetic moments of the proton and neutron are opposite,
corresponding to the magnetic moment of the deuteron. In the absence of orbital
rotation, the entire spin of the deuteron will consist of the nucleons spin.
Considering only the main components of energies and forces, in equilibrium, at
a small distance ![]() between the centers of the nucleons, the
following relations hold:
between the centers of the nucleons, the
following relations hold:
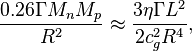
![]()
where ![]() is
the proton radius as the measure of the nucleon radius,
is
the proton radius as the measure of the nucleon radius, 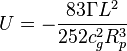 is the internal energy of the torsion
field in the deuteron per one nucleon,
is the internal energy of the torsion
field in the deuteron per one nucleon, 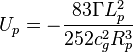 is the internal energy of the torsion field of free nucleon,
is the internal energy of the torsion field of free nucleon, 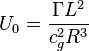 is the
energy of two spins in the field of each other, or doubled energy of one spin
in the external torsion field from the second spin,
is the
energy of two spins in the field of each other, or doubled energy of one spin
in the external torsion field from the second spin, ![]() is the change in rotational kinetic
energy of nucleons,
is the change in rotational kinetic
energy of nucleons, ![]() is the moment of inertia of the nucleon,
is the moment of inertia of the nucleon, ![]() MeV is the binding energy of the deuteron.
MeV is the binding energy of the deuteron.
In the presented balance of forces in the first
approximation only the force of gravitational attraction of nucleons and the
force of spins repulsion ![]() are taken into account. The solution for the
balance of forces and energies is the value
are taken into account. The solution for the
balance of forces and energies is the value ![]() m between the adjacent surfaces of
nucleons. [4] In this case, the particles
of hadron matter inside nucleons on the average have the speed almost equal to
the speed of light.
m between the adjacent surfaces of
nucleons. [4] In this case, the particles
of hadron matter inside nucleons on the average have the speed almost equal to
the speed of light.
Atomic nuclei
The analysis of the equilibrium state of nucleons in the
deuteron allows us to formulate the following conditions for stability of
atomic nuclei:
- Adjacent nucleons must have zero
relative rotation of the surfaces closest to each other. For example, if
nucleons rotate as though located on the same axis, they must rotate
synchronously. Otherwise, magnetic forces and torsion forces appear
leveling the angular rotational velocity.
- Another necessary condition is
that the adjacent nucleons must have such direction of spins that there
was a repulsive force between them.
- The absence of diproton and
dineutron shows that the combination with two adjacent protons or two
neutrons on a common axis of rotation in the nucleus is hardly probable,
at least for small nuclei.
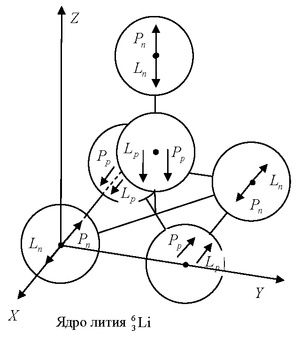
Based on this, the models of triton (tritium nuclei, a
heavy isotope of hydrogen) and of other basic nuclei – helium and lithium are
built. Spin-spin forces between nucleons in atomic nuclei explain the Pauli
exclusion principle, according to which identical fermions that are close,
cannot have the same quantum numbers. In particular, spins of identical
nucleons in the presented models of atomic nuclei are in opposite directions.
It is known that triton turns into the light helium
nucleus with half-decay period 12.32 years due to beta decay. This can be
presented in the way that the left neutron of the triton in Figure P4,
undergoing beta decay, turns into a proton and moves to the position taken by
the left proton in the nucleus of the light helium in Figure P4. In this case, direction of the
nucleon spin does not change, ![]() , but magnetic moment of the
neutron
, but magnetic moment of the
neutron ![]() is transformed into oppositely
directed magnetic moment of the proton
is transformed into oppositely
directed magnetic moment of the proton ![]() .
.
For the motion of the nucleon it needs momentum which
arises from the emission of electron antineutrino in beta decay of the neutron.
As it is shown in the substantial neutron
model, antineutrino flies toward the spin of the decaying neutron and
pushes the neutron in the opposite direction. After this, the triton turns into a nucleus of light helium
Nuclear binding energy
With the help of expression for gravitational energy we
can qualitatively show the need for the growth of specific nuclear binding
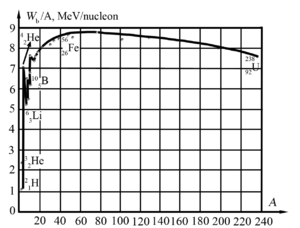
energy (binding energy per nucleon) with growth of mass of the nucleus.
Since in atomic nucleus the nucleon density only slightly
depends on the number of nucleons, it means the approximate equality of volumes
per one nucleon in different nuclei. It is usually assumed that the average
distance between nucleons in nuclei is of the order of ![]() m. If we denote the total binding
energy of nucleus by
m. If we denote the total binding
energy of nucleus by ![]() , with a small number of nucleons this
energy must be proportional to gravitational energy
, with a small number of nucleons this
energy must be proportional to gravitational energy ![]() of all the nucleons of the nucleus in the field of strong gravitation.
of all the nucleons of the nucleus in the field of strong gravitation.
If the nucleus consists of ![]() nucleons, the nuclear mass is
nucleons, the nuclear mass is ![]() ,
the volume per one nucleon is equal to
,
the volume per one nucleon is equal to ![]() ,
the volume of the nucleus is
,
the volume of the nucleus is ![]() , then the nucleus radius
, then the nucleus radius ![]() will be proportional to
will be proportional to ![]() . Hence the specific binding energy and
the specific gravitational energy will be proportional to the quantity:
. Hence the specific binding energy and
the specific gravitational energy will be proportional to the quantity: ![]()
The dependence of the specific binding energy on the
number of nucleons in the nucleus as ![]() in
general is confirmed: if for the deuteron it is equal to 1.1 MeV/nucleon, then
for the nuclei with
in
general is confirmed: if for the deuteron it is equal to 1.1 MeV/nucleon, then
for the nuclei with ![]() the specific binding energy is equal to 8
MeV/nucleon. With further increase of
the specific binding energy is equal to 8
MeV/nucleon. With further increase of ![]() the
specific binding energy reaches the value of 8.7 MeV/nucleon, and then slowly
decreases (approximately up to about 7.6 MeV/nucleon for the nucleus of
uranium). Such a dependence is explained by the growing influence of electrical
energy of protons repulsion with the growth of
the
specific binding energy reaches the value of 8.7 MeV/nucleon, and then slowly
decreases (approximately up to about 7.6 MeV/nucleon for the nucleus of
uranium). Such a dependence is explained by the growing influence of electrical
energy of protons repulsion with the growth of ![]() , which reduces the binding energy. In
addition, from the Le Sage’s theory of gravitation the saturation effect of
strong gravitational energy follows with
, which reduces the binding energy. In
addition, from the Le Sage’s theory of gravitation the saturation effect of
strong gravitational energy follows with ![]() .[4] As a consequence of this effect in case of further increase in the mass of
the nucleus the nucleons added to the nucleus will have the same energy, and
the potential of gravitational field remains almost unchanged. The
gravitational pressure in the nucleus is fixed and stops growing,
correspondingly, the average distances between the nucleons stop changing too.
This result is consistent with the fact that with
.[4] As a consequence of this effect in case of further increase in the mass of
the nucleus the nucleons added to the nucleus will have the same energy, and
the potential of gravitational field remains almost unchanged. The
gravitational pressure in the nucleus is fixed and stops growing,
correspondingly, the average distances between the nucleons stop changing too.
This result is consistent with the fact that with ![]() the maximum of the specific binding energy of
atomic nuclei is reached.
the maximum of the specific binding energy of
atomic nuclei is reached.
Composite hadrons
All hadrons, including mesons and baryons, can be divided
into three groups. The first group includes the simplest quasi-stable hadrons
like pions and nucleons, having long lifetime. These hadrons can be considered
as independent particles experiencing decay due to weak interaction (except for
stable proton). The second group consists of long-lived strange, charmed and
beautiful particles, and the third group includes resonances, whose lifetime is
almost equal to the time of particles’ transit near each other at their close
interaction. As shown in the model of quark
quasiparticles, strange particles can be represented as composite hadrons
of simple hadrons of the first group. [6] For
example, hyperon Λ is assumed to consist of proton and pion rapidly rotating
next to each other along one axis, held by strong gravitation and spin torsion
fields. In calculating the equilibrium conditions, the equations for the forces
and energies are used, similar to those presented above for the deuteron.
Hypothetical composition of other strange hadrons is as
follows: hyperon Σ is a compound of
neutron with pion; Ξ includes proton and two pions; three or four pions with
proton make up Ω-baryon. K-mesons are compounds of three pions and have the
following compositions:
![]()
![]()
![]()
![]()
Different combinations of pions in neutral kaon can
explain different lifetimes of ![]() and
and ![]() states. In contrast to atomic nuclei, compounds of nucleons and pions (or
pions with each other) can not be stable, and over
time they disintegrate. The same applies to charmed and beautiful hadrons.
states. In contrast to atomic nuclei, compounds of nucleons and pions (or
pions with each other) can not be stable, and over
time they disintegrate. The same applies to charmed and beautiful hadrons.
There are many works in which resonances are presented
not as interactions of quarks but as dynamically bound short-lived states of
simpler hadrons. For example, hyperon Λ(1405) is considered as dynamic bound
state of nucleon and kaon, [12] and scalar mesons f(980) and a(980) are considered as a molecule of kaon
and antikaon. [13] Hadronic molecules of kaon, antikaon and nucleon are discussed in [14] by solving the Schrödinger equation for
the wave function of three particles and using two interaction potentials
assumed in the model. There are strong proofs that many resonant states N, Δ,
Λ, Σ, Ξ, Ω are dynamically bound states
of vector mesons (of ρ and ω type) with baryons belonging to baryon octet with
nucleons and to decuplet with Δ. [15]
Weak interaction
In gravitational
model of strong interaction masses as well as charges of elementary particles
are explained by the properties and the structure of particles’ matter, and by
the action of strong gravitation and electromagnetic forces in this matter.
Under the action of these forces ordering of matter particle takes place, and this
matter has the ability to transform slowly in reactions of weak interaction.
Thus weak interaction at the level of elementary particles is reduced again to
weak interaction, but at the level of minute particles that make up the matter
of elementary particles.
The examples of description of reactions of weak
interaction in the matter of elementary
particles are shown in the model of quark
quasiparticles, in the substantial
neutron model and in the substantial
proton model. In particular it is shown that neutrinos of one basic level
of matter are two-component and consist of fluxes of electron neutrinos and
antineutrinos of the lower basic level of matter.
This means that weak interaction can be explained not
with the help of special field quanta of the type of W and Z bosons, but
represent as the property of matter to change naturally in conditions of
maximum possible density of matter and energy.
Thus, it is expected that during the time of the order of 2•1015
years neutron stars must undergo ![]() -decay, with formation of magnetars and
ejection of negatively charged shells (similarly to neutrons decomposing with
formation of protons, electrons and electron antineutrinos).
-decay, with formation of magnetars and
ejection of negatively charged shells (similarly to neutrons decomposing with
formation of protons, electrons and electron antineutrinos).
Coupling constants
Main source: Coupling
constant
To compare gravitational, weak, electromagnetic and
strong interactions the energies of corresponding forces are usually
considered, acting on proton matter taking into account
its mass and charge, in the field of other proton. For energies we can write
down:
![]()
![]()
where ![]() is
gravitational constant,
is
gravitational constant, ![]() is
the proton mass,
is
the proton mass, ![]() is
distance between the centers of protons,
is
distance between the centers of protons, ![]() is
Fermi constant of weak interaction,
is
Fermi constant of weak interaction, ![]() is the speed of light,
is the speed of light, ![]() is
mass of virtual W or Z boson, which is considered the carrier of weak interaction,
is
mass of virtual W or Z boson, which is considered the carrier of weak interaction, ![]() is
the proton charge, equal to elementary charge,
is
the proton charge, equal to elementary charge, ![]() is
electric constant,
is
electric constant, ![]() is
the charge of strong interaction,
is
the charge of strong interaction, ![]() is
the mass of virtual particle (mostly pion), which is supposed carrier of strong
interaction.
is
the mass of virtual particle (mostly pion), which is supposed carrier of strong
interaction.
The expressions for corresponding coupling constants
follow from the relations for energy:
![]()
![]()
The coupling constant of electromagnetic interaction ![]() is
called fine structure constant. The
charge of strong interaction
is
called fine structure constant. The
charge of strong interaction ![]() and the Fermi constant
and the Fermi constant ![]() are axiomatically introduced into Standard theory to describe experimental
results. If we proceed from the notion of strong gravitation, the interaction
energy of two nucleons and the coupling constant will equal: [6]
are axiomatically introduced into Standard theory to describe experimental
results. If we proceed from the notion of strong gravitation, the interaction
energy of two nucleons and the coupling constant will equal: [6]
![]()
where ![]() is
strong gravitational constant,
is
strong gravitational constant, ![]() for the case of two nucleons.
for the case of two nucleons.
This shows that the coupling constant ![]() of
strong gravitation is of the same order of magnitude as the coupling constant
of
strong gravitation is of the same order of magnitude as the coupling constant ![]() of strong interaction. In atomic nuclei the equilibrium of nucleons is
achieved due to attraction from the strong gravitational field and repulsion
from gravitational torsion fields, and the coupling constants of both
components of gravitational field (gravitational field strength of strong gravitation and gravitational torsion field ) are leveled
in magnitude.
of strong interaction. In atomic nuclei the equilibrium of nucleons is
achieved due to attraction from the strong gravitational field and repulsion
from gravitational torsion fields, and the coupling constants of both
components of gravitational field (gravitational field strength of strong gravitation and gravitational torsion field ) are leveled
in magnitude.
Unification of interactions
In Standard model the gauge approach of quantum field
theory is used, when for each type of interaction (gravitational, electromagnetic,
weak and strong) their own fields and gauge bosons-quanta, that carry the
interaction, are introduced. Gravitons, photons, W and Z bosons, gluons, and
particles such as Higgs boson appear this way. At present, weak and
electromagnetic interactions of elementary particles, despite their significant
differences, are discussed by electroweak theory based on the unified
mathematical formalism. In future it is planned to add in the common scheme
strong (Grand Unified Theory) and gravitational interaction (theory of
everything).
Disadvantage of this approach is its focus only on
description of the observed processes, without penetration into the essence of
phenomena. So far, there are no specific mechanisms that explain how the forces
of attraction or repulsion between particles emerge due to the action of any
gauge bosons, such as photons. There is a gap between the facts that single
accelerated charges generate real electromagnetic emission that transfers
energy and theoretically is considered as a set of photons or partial waves,
and there is no such emission near fixed charges although the adjacent charges
somehow interact with each other. To create a unified picture it is necessary
that photons could explain not only free electromagnetic emission but also the
static electromagnetic field. However, in case of purely electrostatic and
magnetostatic fields there are no electromagnetic energy fluxes, the Poynting
vector at each point is zero, and thus the possible direction of the motion of
photons can not be determined. Introducing into the
theory the idea of virtual particles does not help, because interactions with
virtual photons, gluons, W and Z bosons, quark-antiquark pairs,
electron-positron fields, etc. can not be considered
as the ultimate solution.
As shown above, strong interaction at the level of
elementary particles can be reduced to the action of strong gravitation and
spin gravitational forces from torsion fields, with addition from
electromagnetic forces. The same forces and the corresponding interaction will
be at the level of the stars, with substitution of strong gravitation by
ordinary gravitation. It is considered that gravitation at the macro level in
general must be described by relativistic theories such as general theory of
relativity (GTR) or covariant theory of
gravitation (CTG). But in GTR gravitation is reduced to curvature of
spacetime and is not a physical force, whereas in CTG the cause of
gravitational force is assumed the action of gravitons, considered in Le Sage’s
theory of gravitation. Gravitons act on matter regardless of the number and density of this matter and the effects emerging in strong fields near massive bodies, such as the
effect of time dilation, are reduced to influence of gravitons on the
properties of electromagnetic waves (photons) used for measurements. The latter
means dependence of results of measurements of length and time on the
measurement procedure by means of light signals, with the constant picture of
interaction of gravitons with matter. In this case,
the effects of GTR, including the hypothetical black holes, are external, and
do not reflect real essence of gravitational interaction.
In the weak fields, where dependence on the measurement
procedure can be neglected, GTR turns to gravitoelectromagnetism
and CTG – to Lorentz-invariant theory of
gravitation (LITG). It turns out that in LITG and in
gravitoelectromagnetism the equations of gravitational field are almost exactly the same and are similar in form to the equations
of the electromagnetic field in electrodynamics, which is emphasized in Maxwell-like gravitational equations.
Apparently, the similarity of equations for both fields is not accidental.
Relationship between electromagnetism and gravitation may be that part of gravitons are photons
emitted by charged praons – the carriers of matter, from which the matter can be formed, which is part of the matter of elementary particles. [6]
Representation of gravitons in the form of photons was
used to represent the formula of gravitational force, as a result of Compton
scattering of photons in matter. [16] On the other hand, emission of energy of
supernovae in formation of neutron stars is almost entirely realized through
neutrino emission, and not in the form of expected gravitational waves. That,
and the similar penetrating ability of particles give the reason to assume that
neutrinos of one level of matter are gravitational quanta or gravitons of
higher levels of matter. Comparison of the energy density of neutrino emission
in supernova and the similar neutrino emission from matter of neutron which is formed, taking into account the coefficients of
similarity in the theory of similarity of
matter levels, shows that the gravitons of ordinary gravitation can be
neutrinos generated by matter, the carriers of which correspond to
elementary particles in the same way as elementary particles correspond to
stars, or can be smaller by one basic level of matter. [6] If gravitons are both photons and neutrinos, then there is may be the
case when the neutrino is a type of electromagnetic radiation. The difference between photon and
neutrino is that neutrino is two-component emission with opposite polarization
of the components. In this case, photon and neutrino are composed of the
corresponding fluxes of tiny quanta of emission.
In the above picture
electromagnetic and gravitational fields are fundamental and similar to each
other both in the form of equations for the field and the acting forces, and in
their origin associated with the dynamic action of particles of electrogravitational vacuum. For example, gravitational quanta of one
level of matter are able to compress the matter into massive objects of higher level of matter up to such density that as
a result emission of new, more powerful gravitational and electromagnetic
quanta is possible, as well as emission of charged particles such as cosmic
rays. After that, the emerged relativistic particles, neutrinos and photons
interact in a similar way with the matter of higher
levels of matter, and so the process goes on. At the same time, there is a
reverse process of energy dissipation and splitting of quanta.
Adding to the fluxes of gravitons
by Le Sage’s model the fluxes of charged particles of different signs allows us
not only to derive the Newton’s formula of gravitation and to explain the
origin of gravitational force, but also to understand the origin of electrostatic
force between two charges. [17] [2] [18] [19]
Strong and weak interactions by
their nature are not fundamental field interactions, characteristic of each
object separately. This is due to the fact that the first of them depends on combination
of fundamental fields in the interaction of objects with each other, and the
second – on the interaction of internal fields in the matter of objects with the total gravitational and
electromagnetic fields of these objects, or with external emission, leading to matter transformation.
It was shown that the electromagnetic and gravitational fields, acceleration
field, pressure field, dissipation
field, strong interaction field, weak
interaction field, and other vector fields acting on matter and its particles,
are components of general field and can be described by the same equations. [20] [21] Thus, the general field becomes a
good candidate for a unified field theory suitable for describing any
phenomena.
References
- Fedosin S.G. Model
of Gravitational Interaction in the Concept of Gravitons. Journal of
Vectorial Relativity, Vol. 4, No. 1, pp. 1-24
(2009). http://dx.doi.org/10.5281/zenodo.890886 .
- 2.0 2.1 Fedosin S.G. The
graviton field as the source of mass and gravitational force in the
modernized Le Sage’s model. Physical Science International
Journal, ISSN: 2348-0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
- 3.0 3.1 Fedosin S.G. (1999), written at Perm, pages 544, Fizika i filosofiia podobiia ot preonov do metagalaktik,
ISBN 5-8131-0012-1.
- 4.0 4.1 4.2 4.3 4.4
Sergey Fedosin, The physical theories and
infinite hierarchical nesting of matter, Volume 1,
LAP LAMBERT Academic Publishing, pages: 580, ISBN-13: 978-3-659-57301-9.
- Landau L.D. On the theory of stars. – Phys. Z. Sowjetunion, Vol. 1, p. 285
(1932).
- 6.00 6.01 6.02 6.03 6.04
6.05 6.06 6.07 6.08 6.09
Comments
to the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia
vlozhennost’ materii.
– Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref.
289. ISBN 978-5-9901951-1-0. (in Russian).
- Fedosin S.G. The
radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No.
4, pp. 349-363 (2012). http://dx.doi.org/10.5281/zenodo.889451.
- 'Perfect'
Liquid Hot Enough to be Quark Soup. Brookhaven National Laboratory
News (2010). Retrieved on 2010-02-26.
- LHC
Experiments Bring New Insight into Primordial Universe. Brookhaven
National Laboratory News (2010). Retrieved on 2010-12-09.
- Ishii N., Aoki S., Hatsuda
T. The Nuclear Force from
Lattice QCD. arXiv: nucl-th
/ 0611096 v1, 28 Nov 2006.
- Яворский
Б.М., Детлаф А.А., Лебедев А.К. Справочник по
физике. – М.: Оникс, Мир и образование, 2006, 1056 с.
- R. H. Dalitz and S. F. Tuan, Phys. Rev. Lett. Vol. 2, p. 425 (1959); Annals Phys. 10, 307
(1960).
- J.D. Weinstein and N. Isgur, Phys. Rev. Lett. 48,
659 (1982); Phys. Rev. D 41, 2236 (1990).
- Daisuke Jido, Yoshiko
Kanada-En'yo. A new N* resonance as a hadronic
molecular state. 25 Jun 2009.
- Oset, E. at al. Dynamically generated resonances.
20 Jun 2009.
- Michelini Maurizio. The Physical
Reality Underlying the Relativistic Mechanics and the Gravitational
Interaction. – arXiv: physics / 0607136 v1,
14 Jul 2006.
- Fedosin
S.G. Fizicheskie
teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0.
(in Russian)
- Fedosin S.G. The
charged component of the vacuum field as the source of electric force in
the modernized Le Sage’s model. Journal of Fundamental and Applied
Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18,
https://dx.doi.org/10.5281/zenodo.845357.
- Fedosin
S.G. On the structure of the force field in electro gravitational vacuum.
Canadian Journal of Pure and Applied Sciences, Vol. 15, No. 1, pp.
5125-5131 (2021). http://doi.org/10.5281/zenodo.4515206.
- Fedosin S.G. The Concept of the General
Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
- Fedosin
S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1,
No. 2, 1750002, 9 pages (2017).
http://dx.doi.org/10.1142/S2424942417500025.
See also
- Infinite
Hierarchical Nesting of Matter
- Similarity
of matter levels
- SPФ
symmetry
- Strong
gravitation
- Gravitational
torsion field
- De Broglie
wavelength
- Model of
quark quasiparticles
- Substantial electron model
- Substantial neutron model
- Substantial
photon model
- Substantial
proton model
- Praon
External links
|
||||||