Electrogravitational
vacuum
The electrogravitational vacuum describes properties of the
physical vacuum and the cosmic space devoid of matter based on the modernized Le Sage’s theory of gravitation and implies that the vacuum is filled with particles
called gravitons and with tiny charged particles. Some of these particles have
a large Lorentz factor, similarly to ultra-high-energy cosmic rays, which
imparts a dynamic character to the vacuum. Due to high penetrating capacity
when moving in the matter, these particles are considered to be responsible for
the emergence of gravitational [1] [2] [3] and
electromagnetic [4] [5] forces between bodies. In
addition, photons and neutrinos can consist of these particles. [6]
The composition of these particles and their properties are determined using
the theory of Infinite Hierarchical Nesting of Matter,
the similarity of matter levels and SPФ symmetry. In particular, fluxes of charged particles
such as praons are assumed to be the
main active component of the electrogravitational vacuum. [7]
Contents
- 1 Existing
models of vacuum
- 2
Description of the electrogravitational vacuum model
- 2.1
Composition of the vacuum’s particles
- 2.2
Physical parameters of the vacuum particles
- 2.3
Gravitational field
- 2.4
Electromagnetic field
- 2.5
Interaction of the vacuum’s particles with the matter
- 2.6
Emergence of the relativistic vacuum’s particles
- 2.7
Photons
- 2.8
Strong interaction
- 2.9 Weak
interaction
- 2.10
Neutrinos
- 3
Cosmology
- 4 Extended special theory of relativity
- 5 General
field
- 6 Preferred reference frames
- 7 References
- 8 See also
- 9 External links
Existing
models of vacuum
In physics, there are numerous
models suggested to define the vacuum characteristics. Thus, the vacuum of free
space, in which the laws of classical electromagnetism hold true, should
satisfy the following conditions:
- The speed
of propagation of electromagnetic waves equals the speed of light.
- The
superposition principle is satisfied, when the four-potential and the
electromagnetic tensor at any point of a system is calculated respectively
in terms of the scalar or vector sum of the components of the four-potentials
and the electromagnetic tensors of all the charged particles of the
system.
- The vacuum permittivity is equal to the electric
constant, and the
magnetic permeability is equal to the magnetic constant or the vacuum
permeability.
- The
characteristic impedance equals the impedance of free space.
In the Lorentz-invariant theory of gravitation the vacuum is characterized as follows:
- The speed
of propagation of gravitational waves equals the speed of gravity, which,
in the first approximation, equals the speed of light.
- For the gravitational four-potential and the gravitational
tensor the superposition principle
is satisfied.
- The gravitational interaction is characterized by
the gravitational constant.
- For gravitation, the gravitoelectric constant,
the gravitomagnetic constant, and the gravitational characteristic impedance of free
space can be defined.
The above characteristics of the
classical vacuum are presented in the article on the vacuum constants.
In the General Relativity, the vacuum solution (general relativity) can be obtained when the gravitational field in the
absence of the electromagnetic field is calculated in the empty space outside
the matter, where the stress-energy tensor of the matter and non-gravitational
fields is equal to zero. Despite the equality of this tensor to zero, in the
empty space there still can be curvature of spacetime, which, through the
metric tensor and its derivatives, defines the effect of gravitation from some
local or global source. Besides, variations in solutions are possible, which
depend on taking into account the cosmological constant and the choice of its
sign. Due to the connection with the metric tensor, the gravitational field in
this theory is a tensor field.
Its own vacuum is also assumed
within the covariant theory of gravitation, in which the gravitational field is a vector field,
since it is given by the four-potential and the gravitational tensor. In this
case, the connection between gravitation and geometry, between the
gravitational field and the metric tensor, which is characteristic of the
general theory of relativity, is broken. The gravitational field is assumed to
be physical interaction, which, just as electromagnetic interaction, becomes
independent of the metric tensor that characterizes the properties of the
spacetime depending on the parameters of the source of the gravitational field.
The source of the gravitational field here means some material object or
physical system of matter and its proper fields, and the vacuum is treated as
the contents of the space outside the system’s matter. For infinite space that
does not contain a visible source of the gravitational field, it follows from
the field equations that the gravitational field
strength ![]() and the gravitational torsion field
and the gravitational torsion field ![]() in the simplest case are constant vectors
that do not depend on time. Provided that
in the simplest case are constant vectors
that do not depend on time. Provided that ![]() and
and ![]() in such a space the scalar potential
in such a space the scalar potential ![]() and the vector potential
and the vector potential ![]() of the gravitational field should be constant
values, independent of the coordinates and time. Thus, it can be assumed that
in the vacuum, far from the sources of the gravitational field, both the
four-potential and the gravitational tensor vanish. Another peculiarity of this
vacuum is that, due to gauging of the system’s relativistic energy and the
equation for the metric, outside the matter both the cosmological constant and
the scalar curvature vanish. [8] Meanwhile in the relativistic uniform system both the cosmological constant and the scalar
curvature inside the matter turn out to be constant values.
of the gravitational field should be constant
values, independent of the coordinates and time. Thus, it can be assumed that
in the vacuum, far from the sources of the gravitational field, both the
four-potential and the gravitational tensor vanish. Another peculiarity of this
vacuum is that, due to gauging of the system’s relativistic energy and the
equation for the metric, outside the matter both the cosmological constant and
the scalar curvature vanish. [8] Meanwhile in the relativistic uniform system both the cosmological constant and the scalar
curvature inside the matter turn out to be constant values.
In quantum physics, the basic
quantity is the Planck constant as a typical quantity of action for any
particles under consideration. Taking this quantity into account changes the
vacuum properties required for the theory. Thus, in quantum electrodynamics, it
is assumed that the electromagnetic interaction between the charged particles
occurs by means of photons as the carriers of interaction. This means that the
charged particles must absorb and emit photons in order to change their energy
and momentum. QED vacuum is assumed to
be filled with various virtual particles, including short-lived photons and
electron-positron pairs. Virtual particles define zero-point oscillations of
the vacuum as its ground state. The energy of the vacuum’s zero-point
oscillations is called zero-point energy, its
exact magnitude is unknown. It is supposed that a change in zero-point energy
with a change in the system’s configuration in the vacuum leads to the Casimir effect. Under the influence of the electromagnetic field,
the vacuum polarization takes place and various subtle effects can occur. In
this case, the vacuum will become diamagnetic, so that the relative magnetic
permeability will be less than unity. The vacuum also exhibits dielectric
properties, since the relative permittivity is greater than unity.
One of the problems of such
vacuum is that zero-point energy, which is estimated to have a very large
magnitude, does not manifest itself as the source of the gravitational field
and is not part of the mathematical apparatus of the general theory of
relativity. This leads to the problem of discrepancy between the vacuum’s zero-point
energy and the observed small value of the cosmological constant, which is
known as the cosmological constant problem.
The vacuum of quantum
chromodynamics is considered to be filled with gluon condensate and fermionic condensate of quarks. Both condensates can give mass to
elementary particles and hadrons, and fermionic condensate possesses
superfluidity. The condensates should have such properties that the color confinement and hadrons’ masses could be explained.
QED vacuum and QCD vacuum are the constituent parts of the vacuum in the Standard Model, which, however, does not take into account
gravitation.
The superfluid vacuum, containing
some superfluid or Bose-Einstein condensate, is viewed as the basis for quantum-based unification
of all the four fundamental interactions, including weak interaction, strong interaction, electromagnetic interaction, and gravitational interaction. The fluid is assumed to consist of
fermion-antifermion pairs and is described with the help of macroscopic wave
function. Interaction of the fluid with elementary particles gives mass to the
latter. At low energies and momenta of the fluid fluctuations, treated as
virtual particles, this fluid is considered an ideal one, leading to Lorentz covariance.
However, attempts to present gravitation as a consequence of the relativistic
motion of the fluid fluctuations did not produce a result. The probable reason
for this is said to be the fact that the macroscopic curvature of spacetime in
the general theory of relativity can be the long-wavelength limit that does not
work on the small scales of quantum gravitation.
Unfortunately, all the vacuum
models presented above mainly describe its properties, which are required in
one or another theory. As for the substantial component of the vacuum, which
defines its structure and represents the specific carriers that determine the
characteristics of the vacuum, the information here is either missing or
extremely speculative.
Description
of the electrogravitational vacuum model
Composition
of the vacuum’s particles
The electrogravitational vacuum model
is based on the theory of Infinite
Hierarchical Nesting of Matter,
which considers the universe from the point of view of scale dimension, SPФ symmetry, similarity of matter levels and quantization of parameters of cosmic systems. On the scale axis all objects of the universe can be
placed, which are grouped into matter levels. Each basic level of matter has
its own most dense and long-lived objects with the maximum energy density, with
strong gravitational, electric and magnetic fields. At the level of stars these
objects are neutron stars, at the atomic level they are nucleons. Neutron stars
consist of nucleons, and by analogy nucleons consist of praons, and praons
consist of graons. Praons and graons have their own levels of matter, similar
to the nucleon level of matter.
In the electrogravitational
model, the vacuum includes a set of the densest objects of an infinite number
of those matter levels that are below the matter level corresponding to the
observer. For a human observer the main components of the physical vacuum are
individual nucleons, praons, graons and even smaller particles, as well as
complex and composite objects that consist of them. For example, atomic nuclei
consist of nucleons, and we can conceive similar nuclei of praons or graons. It
is assumed that ordinary photons emitted by atoms consist of praons, and the
neutrinos observed in experiments consist of graons. [6] Since the
masses of the main objects in the chain of matter levels: neutron
star-nucleon-praon-graon -... are rapidly decreasing, it is obvious that at
present it is quite difficult to detect and register in the vacuum individual
praons or individual photons consisting of graons.
If the observer belonged to the
metagalactic level of matter, then for him the vacuum would also contain such
objects as neutron stars, white dwarfs, ordinary main sequence stars and
planets. All these objects are composed of nucleons and have their analogues on
the nucleon level of matter. Thus, the analogue of a white dwarf from the point
of view of the matter evolution under the action of gravitation is a nuon, and
from the point of view of the matter’s radioactive decay the analogue of a
white dwarf is a muon. The neutron star of the lowest possible mass is the
analogue of a pion.
In addition to nucleons, the
matter also contains electrons, the analogues of which at the level of stars
are discons, that is, massive discs discovered in some neutron stars and
magnetars. [9] [10] Discons, just as the stars
themselves, can carry an electric charge. A magnetar with a positive charge and
a discon with a negative charge are analogous to a hydrogen atom in the hydrogen system.
Galaxies correspond to the smallest dust particles, in the center of which
there is solid matter and on the outside, there is thick gaseous shell of the
different atoms. The latter analogue becomes thicker over time, since the stars
in the galaxies evolve and turn into neutron stars and white dwarfs. In this
picture magnetars are formed from neutron stars, just as protons are formed in free neutron decay. The
matter of discons in its density and composition must be close to the density
and composition of planets and must contain mainly elements like iron and other
metals. Since all stars, planets and discons are composed of nucleon matter,
under appropriate conditions all these objects can be transformed and generate
each other.
Objects like discons and
electrons must be present at every level of matter, forming together with the
main objects the corresponding matter. For example, elementary particles
(nucleons, electrons, hadrons and leptons) must consist of praons and
praelectrons just as stars and planets consist of nucleons and electrons. This allows
elementary particles to transform into each other. The similarity between the
matter levels allows us to construct the models of elementary particles, such
as the substantial neutron model, the substantial proton
model, the substantial electron model, the substantial photon
model.
We assume that black holes do not
exist, as they are attributed the property of absorbing matter and do not
letting anything out. But this contradicts the fact that the graviton field
penetrates all bodies, and thereby creates gravitational phenomena. If a black
hole would only absorb the energy of graviton fluxes, it would acquire in a
short time a huge amount of mass-energy and should grow indefinitely in size,
which is not observed.
The highly rarefied vacuum of
cosmic space outside the dust and gas clouds may contain:
- Nucleons
with concentration of the order of several pieces per cubic meter. Some of
these nucleons can be in the form of an atomic or molecular gas, in the
form of ions and atomic nuclei, as well as in the form of relativistic
particles of cosmic rays.
- Electrons
in a number close to that which ensures the vacuum electroneutrality.
- Photons.
- Neutrinos.
- Elementary
particles – pions, muons, etc.
- Gravitational
and electromagnetic fields.
By analogy, from the point of
view of a human observer the electrogravitational vacuum must contain all those
smallest objects that either cannot be directly registered in the experiment,
or are the sources generating the gravitational and electromagnetic fields, and
are also causing strong and weak interactions. Thus, this vacuum includes
praons, graons and even smaller particles, as well as objects consisting of
them, which have smaller masses and energies than the known elementary
particles.
Physical
parameters of the vacuum particles
In order to determine the
parameters of the vacuum particles the similarity theory is used. A typical
neutron star has a mass of 1.35 solar masses, a radius of about 12 km, and the characteristic speed of the particles’ motion in such a star reaches the
value of 0.23 the speed of light. Dividing these quantities by the
corresponding quantities for the proton, we find the coefficients of
similarity: in mass Ф = 1.62∙1057 , in size Р
= 1.4∙1019 , in speed S = 2.3∙10-1 . In the first
approximation, we can assume that the same coefficients of similarity in mass
and size are also valid for the relation between praons and nucleons. Hence we can determine the praon’s
mass ![]() kg and radius
kg and radius ![]() m. Using the praon’s
mass and radius, we can estimate the average density of its matter
m. Using the praon’s
mass and radius, we can estimate the average density of its matter ![]() kg/m3 .
kg/m3 .
The characteristic speed of the
particles of the matter inside a proton and a praon is quite close to the speed
of light. If at the center of a neutron star the Lorentz factor reaches the
value ![]() then at the
center of a proton the Lorentz factor for the praons located there is equal
to
then at the
center of a proton the Lorentz factor for the praons located there is equal
to ![]() [11] Hence it follows that the coefficient of
similarity in speed for the levels of nucleons and praons is close to unity,
[11] Hence it follows that the coefficient of
similarity in speed for the levels of nucleons and praons is close to unity, ![]() . Taking this into account it is possible to
determine the gravitational constant
. Taking this into account it is possible to
determine the gravitational constant ![]() acting on the praon level of
matter. The similarity relations between the levels of praons and nucleons
give:
acting on the praon level of
matter. The similarity relations between the levels of praons and nucleons
give: 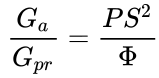 , and therefore
, and therefore
![]() m3•s–2•kg–1.
m3•s–2•kg–1.
The Boltzmann constant for the
level of praons at ![]() is given by the expression:
is given by the expression: 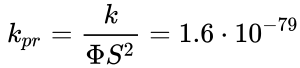 J/K , where
J/K , where ![]() is the Boltzmann constant.
is the Boltzmann constant.
If we calculate the kinetic
energy of a proton ![]() as for a
certain typical particle moving at the center of a neutron star, then using the
equality
as for a
certain typical particle moving at the center of a neutron star, then using the
equality 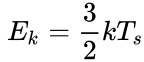 we can
estimate the maximum temperature at the center of a star:
we can
estimate the maximum temperature at the center of a star: ![]() K. Similarly,
the temperature at the center of a proton will be
K. Similarly,
the temperature at the center of a proton will be 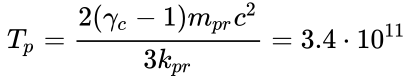 K.
K.
The typical angular momentum at
each level of matter is given by the corresponding Dirac constant. For compact
stars the stellar Dirac constant is ![]() J∙s, for the
nucleon level of matter the Dirac constant is
J∙s, for the
nucleon level of matter the Dirac constant is ![]() J∙s, while the quantum spin of a nucleon is
equal to
J∙s, while the quantum spin of a nucleon is
equal to ![]() . In order to estimate the Dirac constant
. In order to estimate the Dirac constant ![]() at the level of praons, the similarity
relation is applied:
at the level of praons, the similarity
relation is applied: 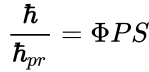 . If the
coefficient of similarity in speed is
. If the
coefficient of similarity in speed is ![]() , then we obtain
, then we obtain ![]() J∙s. Then from the similarity theory it
follows that the photons of the praon level of matter have energies
J∙s. Then from the similarity theory it
follows that the photons of the praon level of matter have energies ![]() less than the energies of the
corresponding photons of the nucleon level of matter. Accordingly, we can say
approximately the same with respect to the difference between the energies of
relativistic graons, relativistic praons and high-energy cosmic rays. It is
assumed that graons are responsible for strong gravitation, and praons are
responsible for ordinary gravitation, while the Dirac constant for graons is
substantially less than the Dirac constant
less than the energies of the
corresponding photons of the nucleon level of matter. Accordingly, we can say
approximately the same with respect to the difference between the energies of
relativistic graons, relativistic praons and high-energy cosmic rays. It is
assumed that graons are responsible for strong gravitation, and praons are
responsible for ordinary gravitation, while the Dirac constant for graons is
substantially less than the Dirac constant ![]() for praons. The picture described above
differs fundamentally from the quantum gravitation approach, which considers
gravitons as objects that necessarily have a spin in the form of the Dirac
constant
for praons. The picture described above
differs fundamentally from the quantum gravitation approach, which considers
gravitons as objects that necessarily have a spin in the form of the Dirac
constant ![]() .
.
For the strong gravitational constant the following relation holds true:
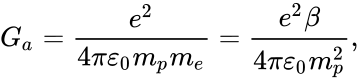
where ![]() is the elementary charge,
is the elementary charge, ![]() is the electric constant,
is the electric constant, ![]() is the proton mass,
is the proton mass,
![]() is the electron mass,
is the electron mass, 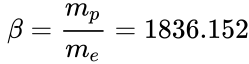 is the ratio
of the proton mass to the electron mass.
is the ratio
of the proton mass to the electron mass.
Similarly, at the level of praons
we have the following:
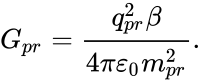
Hence we find the praon charge ![]() C.
C.
Acting similarly, we can obtain
the parameters of graons and other vacuum particles.
Gravitational
field
In the model under consideration,
the gravitation effect arises under the action of gravitons – the smallest
relativistic vacuum particles that fill the whole space and act within the
framework of the modernized Le Sage’s theory.
Besides, each basic level of matter is characterized by its own gravitational
constant. For the level of stars it is the ordinary gravitational constant, and for the nucleon level of matter it is the strong gravitational constant. [12] The particles of the graon level of
matter are assumed to be responsible for the effect of strong gravitation,
which holds nucleons and elementary particles in integrity, and the particles
of the praon level of matter are responsible for the ordinary gravitation.
The gravitons can be both neutral
particles, such as neutrinos and photons, and relativistic charged particles,
similar in their properties to cosmic rays. The effective mass of all these
particles is their relativistic mass-energy, taking into account the great in
magnitude Lorentz factor. In particular, the gravitons can be the praons
accelerated by the strong fields near nucleons almost to the speed of light. As
part of the graviton field, such relativistic praons can participate in
creation of ordinary gravitation, according to the Le Sage’s model, and give
mass to the bodies at the macrolevel. In this case, the praons have their own
rest mass, which arises from the action of the gravitons of lower levels of matter.
During interaction with the fields and the matter, relativistic praons can
produce high-energy photons, which can also serve as the particles of the
graviton field. The energy of ordinary photons is proportional to their
frequency and the Planck constant. But for the particles belonging to different
levels of matter, the value of the Planck constant varies considerably
according to the infinite nesting of matter – the lower is the level of matter,
the less is the respective Planck constant and the lower is the energy of
photons at this level of energy. As a result, the graviton field represents a
multi-component system of particles, photons and neutrinos, the energies of
which are associated with each of an infinite number of matter levels.
The energy density of graviton
fluxes responsible for gravitation in the model of cubic distribution of the
fluxes of particles in space equals: [2] [5]
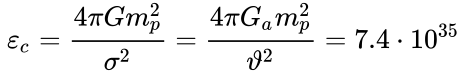 J/m 3,
J/m 3,
where ![]() is the gravitational constant,
is the gravitational constant, ![]() is the proton mass,
is the proton mass, ![]() m2 is the cross-section of
interaction of gravitons with the matter for the ordinary gravitation,
m2 is the cross-section of
interaction of gravitons with the matter for the ordinary gravitation,
![]() m3•s–2•kg–1 is the strong gravitational constant,
m3•s–2•kg–1 is the strong gravitational constant, ![]() m2
is the cross-section of interaction of the vacuum’s charged particles
with nucleons during electromagnetic interaction. In this case, the relation
holds:
m2
is the cross-section of interaction of the vacuum’s charged particles
with nucleons during electromagnetic interaction. In this case, the relation
holds: 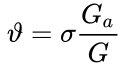 .
.
The obtained value of the energy
density of the graviton fluxes defines the field mass-energy limit and exceeds the rest energy density of the proton 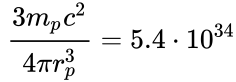 J/m3
, with the proton radius
J/m3
, with the proton radius ![]() m according to the article. [13]
m according to the article. [13]
The flux of gravitons’ energy in
one direction has the value of the order of ![]() W/m2.
If gravitons represented the electromagnetic field quanta, then for the
temperature of the field of gravitons in the form of photons we can get an
estimate
W/m2.
If gravitons represented the electromagnetic field quanta, then for the
temperature of the field of gravitons in the form of photons we can get an
estimate ![]() K.
K.
The expressions for the
gravitational field strengths inside and outside the ball, obtained in the
model of gravitons, are in good agreement with the values of the field
strengths in the Lorentz-invariant theory of gravitation. [2] Going
from field strengths to field potentials, using Lorentz transformation, introducing gravitational
four-potential, one
can find gravitational
stress-energy tensor, the
gravitational field equations, the gravitational force, as well as the
contribution of the gravitational field into the equation for the metric. This
means that the gravitational field theory both in the flat Minkowski space and
in the curved spacetime is fully proved at the substantial level through the
graviton field. And the dependence of metric on the gravitational field
potential allows us to take into account the influence of the inhomogeneous
graviton field on the results of space-time experiments, based as a rule on the
use of electromagnetic waves and devices.
As for the value of the limiting
force of attraction between two contacting massive bodies, the following value
was found: [1]
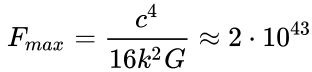 N,
N,
which implies the case when the
graviton fluxes are completely retained by these bodies.
Here ![]() is the speed of light,
is the speed of light, ![]() for the case of uniform density. If we divide
for the case of uniform density. If we divide
![]() by the mass of a typical neutron star, which
is equal to
by the mass of a typical neutron star, which
is equal to ![]() solar masses, we will obtain the acceleration
solar masses, we will obtain the acceleration
![]() m/s2.
For comparison, the gravitational acceleration on the surface of this star,
with its radius
m/s2.
For comparison, the gravitational acceleration on the surface of this star,
with its radius ![]() km, is equal to
km, is equal to ![]() m/s2.
m/s2.
The difference between the
Newton’s formula for the force ![]() of attraction between two neutron stars in
their contact and the formula that takes into account the scattering of
gravitons in the stars’ matter due to the high density of the matter leads to
reduction of the acting force to the value
of attraction between two neutron stars in
their contact and the formula that takes into account the scattering of
gravitons in the stars’ matter due to the high density of the matter leads to
reduction of the acting force to the value ![]() . [3]
. [3]
The presented model describes how
bodies acquire mass as a measure of inertia. The body mass can be expressed in
terms of the luminosity of those graviton fluxes that interacted with the body
matter and transferred their momentum to it. In this case, the graviton
luminosity is proportional and almost equal to the rest energy of the body,
released from the body per time of gravitons’ passing the radius of the body.
The body mass at a constant volume is proportional to the concentration of
nucleons, and similarly the number of interactions of gravitons with nucleons
increases with increasing of concentration of nucleons. Thus, the body’s
inertia as the resistance to the applied force and gravitational mass of the
body are caused by the action of the graviton field on the given body. As it follows
from the principle of relativity, at a constant velocity the action of graviton
fluxes from different sides is balanced, but it is not so in case of the body’s
acceleration. When the body is accelerated, a force must be applied and work
must be carried out to bring the body from the state with one velocity into the
state with a different velocity. This work is done against the action of
gravitons fluxes and leads to the concept of mass as a measure of the body’s
inertia proportional to the applied force and inversely proportional to the
emerging acceleration. The gravitational mass is determined from the
expressions for the gravitational field’s strength and potential, and therefore
it differs from the inertial mass of the body, since the latter takes into
account the contributions to the mass from all the body’s proper fields. In the
relativistic uniform system, it is found that the inertial mass is less than the
gravitational mass, ![]() [14] [15]
[14] [15]
As a rule, the majority of
gravitons pass through matter without losing their energy and momentum. Thus,
the estimate of the total graviton luminosity of a neutron star as the power of
the energy fluxes of gravitons passing through the star gives the value of the
order of ![]() W. If we
calculate the average luminosity of those gravitons that interact with each
nucleon of the matter and transfer their momentum to it, we obtain the
following: [2]
W. If we
calculate the average luminosity of those gravitons that interact with each
nucleon of the matter and transfer their momentum to it, we obtain the
following: [2]
![]() W.
W.
The meaning of this value at
first glance is not quite clear. However, with the help of the similarity
coefficients we can calculate a similar value at the level of stars – the
luminosity of those gravitons that interact with each neutron star and impart
mass to it due to the loss of their momentum:
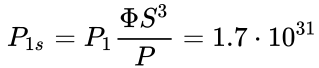 W.
W.
In physics, there is such a known
quantity as Eddington luminosity, which means the limiting luminosity of a star. When
this luminosity is exceeded, the star begins to lose mass due to ejection of
the matter from the surface under the action of the radiation from the star. If
a neutron star with the mass ![]() , where
, where ![]() is the mass of the Sun, has ionized hydrogen
in its atmosphere, then the Eddington luminosity for it would be equal to
is the mass of the Sun, has ionized hydrogen
in its atmosphere, then the Eddington luminosity for it would be equal to 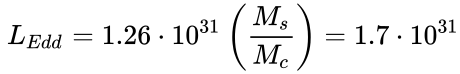 W.
W.
The coincidence of the quantities
![]() and
and ![]() seems surprising, but it is not accidental,
since both quantities have limiting character and are associated with the
integrity of the neutron star as such. Due to
seems surprising, but it is not accidental,
since both quantities have limiting character and are associated with the
integrity of the neutron star as such. Due to ![]() the star does not only gain mass as a measure
of inertia in the graviton fluxes, but also acquires quite definite
distribution of pressure and temperature in the matter, reaching a maximum at
the center. Solving the equations of the acceleration field
allows us to calculate the dependence of the Lorentz factor of the particles’
motion inside the star as a function of the current radius. [16] The
star cannot cool down below the limit, which is set by the graviton fluxes for
each state of matter, and therefore it always has a certain minimum degree of
heating of this matter, the corresponding binding energy, potential
gravitational energy and gravitational acceleration. Under the action of
gravitational acceleration, the nucleons are forced against the surface of the
star, but if the star has radiation luminosity
the star does not only gain mass as a measure
of inertia in the graviton fluxes, but also acquires quite definite
distribution of pressure and temperature in the matter, reaching a maximum at
the center. Solving the equations of the acceleration field
allows us to calculate the dependence of the Lorentz factor of the particles’
motion inside the star as a function of the current radius. [16] The
star cannot cool down below the limit, which is set by the graviton fluxes for
each state of matter, and therefore it always has a certain minimum degree of
heating of this matter, the corresponding binding energy, potential
gravitational energy and gravitational acceleration. Under the action of
gravitational acceleration, the nucleons are forced against the surface of the
star, but if the star has radiation luminosity ![]() , which is equal to the luminosity of the
gravitons
, which is equal to the luminosity of the
gravitons ![]() , the nucleons
acquire additional energy. This energy would be just enough for the star to
lose mass due to evaporation of nucleons from the surface.
, the nucleons
acquire additional energy. This energy would be just enough for the star to
lose mass due to evaporation of nucleons from the surface.
Electromagnetic
field
The presence in vacuum of
relativistic charged particles helps to explain the mechanism of attraction and
repulsion between the charges of different and opposite signs, [3]
which acts similarly to the Fatio-Le Sage's mechanism for the force of
gravitational attraction of masses. This implies the same form of laws in the
Coulomb force for the charges and in the Newton force for the masses, as well
as the similarity of Maxwell's equations and the equations of the gravitational
field in Lorentz-invariant theory of
gravitation. [12]
The interaction picture is shown
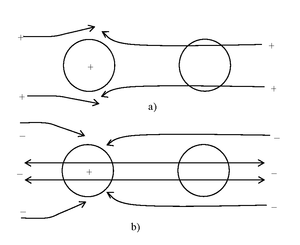
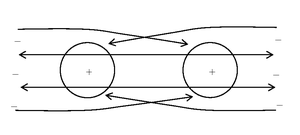
in Figures 1, 2, 3.
Fig.1. The lines of motion of the small particles of the vacuum, which are
a) positively charged, b) negatively charged, near two bodies one of which is
neutral and the other is positively charged.
Fig.2. The lines of motion of the small particles of the vacuum which are
a) positively charged, b) negatively charged, near two bodies, one of which is
negatively charged and the other is positively charged.
Fig.3. The lines of motion of the small particles of the vacuum, which are
negatively charged, near two positively charged bodies.
Figure 1 shows the motion of
small charged particles of the vacuum near the two bodies, one of which is
neutral and the other is positively charged. As can be seen, both positive and
negative particles act symmetrically on the positively charged body, which does
not result in emerging of any additional force in comparison with the force of
gravitation. The same applies to the second neutral body. Figure 2 a) shows
that the positive particles push the negatively charged body to the left, and
Figure 2 b) shows that the negative particles push the positively charged body
to the right (when the smallest particles pass through the body similarly to
gravitons, they transfer their momentum to them). Consequently, both bodies will
be attracted to each other.
Figure 3 shows the lines of
motion of the negative particles of the vacuum near two positively charged
bodies. Both bodies attract the negative particles and obtain an additional
momentum from them, which leads to repulsion of bodies. The motion of the
positive particles of the vacuum in Figure 3 is not shown. It is assumed that
they are repelled from the bodies and therefore their interaction with them is
weak. For two negatively charged bodies the interaction is similar to the one
shown in Figure 3, only it is necessary to replace the signs of all charges.
This results in the repulsion of similarly charged bodies. The common in all
the Figures is the fact that depending on the sign of the charge of two bodies
the number of charged particles falling on the body changes so that after
calculating the momentum transferred from these particles the electric force
with required direction emerges. Thus, we reduce the interaction between the
charges at a distance to the interaction by means of the charged particles of
the vacuum.
The energy density of the fluxes
of the vacuum’s charged particles, responsible for the occurrence of the
electric force between the charged bodies, in the model of the cubic
distribution of the fluxes of particles in space is equal to: [5]
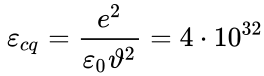 J/m3,
J/m3,
where ![]() is the electric constant,
is the electric constant, ![]() is the elementary charge,
is the elementary charge, ![]() m2 is the cross-section of
interaction of the vacuum’s charged particles with nucleons.
m2 is the cross-section of
interaction of the vacuum’s charged particles with nucleons.
The energy flux of the vacuum’s
charged particles in one direction is of the order of ![]() W/m2.
Estimation of the concentration of the vacuum’s charged particles in the form
of the concentration of relativistically moving praons gives the value
W/m2.
Estimation of the concentration of the vacuum’s charged particles in the form
of the concentration of relativistically moving praons gives the value
![]() m–3, and the Lorentz factor reaches
the value
m–3, and the Lorentz factor reaches
the value ![]() .
.
The limiting current density as
the current density in vacuum in one direction, emerging from the flux of
positively charged praons in case of cubic distribution, is equal to:
![]() A/m2.
A/m2.
In books [3] [12]
the assumption is made that some neutron stars – magnetars can have a positive
electric charge of up to ![]() C, where
C, where ![]() is the elementary electric charge and the
similarity coefficients are used in accordance with the dimensional analysis.
The charge of the star can also be determined by the formula similar to the
formula for the strong gravitational constant. This gives the following:
is the elementary electric charge and the
similarity coefficients are used in accordance with the dimensional analysis.
The charge of the star can also be determined by the formula similar to the
formula for the strong gravitational constant. This gives the following:
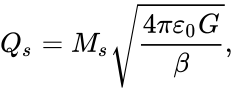
where the magnetar’s mass equals ![]() solar masses,
solar masses, ![]() is the ratio of the proton mass to the
electron mass.
is the ratio of the proton mass to the
electron mass.
In this case, the electric force
of repulsion acting on one proton on the surface of the charged star would
equal 55 N, which is much greater than the gravitational force of attraction of
the proton to the star. However the magnetar looks like a huge atomic nucleus
consisting of a number of closely-spaced nucleons. The balance of attractive
and repulsive forces, arising from strong gravitation in gravitational model
of strong interaction, can
be responsible for the integrity of the atomic nuclei, as well as for the
integrity of the charged neutron star. Besides, the proton charge and the
magnetar charge are limiting values, which means that an increase in these
charges would lead to destruction of these objects.
In a magnetar, the average
concentration of nucleons is ![]() m–3,
and the average concentration of the positive charge is
m–3,
and the average concentration of the positive charge is ![]() m–3.
In view of the Beer–Lambert law, the flux of
gravitons decreases exponentially as it moves through the matter:
m–3.
In view of the Beer–Lambert law, the flux of
gravitons decreases exponentially as it moves through the matter: ![]() , here
, here 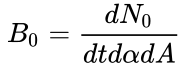 is the number
of gravitons
is the number
of gravitons ![]() entering the matter from the vacuum through
the area
entering the matter from the vacuum through
the area ![]() over time
over time ![]() from the solid angle
from the solid angle ![]() . Similarly, the flux of charged particles
decreases exponentially as it moves through the charged matter:
. Similarly, the flux of charged particles
decreases exponentially as it moves through the charged matter: ![]() .
.
Assuming that ![]() km, for the
exponents it turns out:
km, for the
exponents it turns out: ![]() ,
, ![]() . It follows
that if we put three neutron stars in the way of the flux of gravitons, the
flux will reduce approximately by a factor of
. It follows
that if we put three neutron stars in the way of the flux of gravitons, the
flux will reduce approximately by a factor of
![]() , where
, where ![]() is Euler's number
as the base of the natural logarithm. But for the flux of charged particles of
the vacuum in order to reduce it noticeably we need to put in a line about 140
magnetars.
is Euler's number
as the base of the natural logarithm. But for the flux of charged particles of
the vacuum in order to reduce it noticeably we need to put in a line about 140
magnetars.
This difference in fluxes allows
us to explain the saturation effect of the specific binding energy, when the
nuclear binding energy per nucleon, depending on the number of nucleons in
nuclei, first increases, reaching a maximum of 8.79 MeV per nucleon for the
nucleus ![]() , and then begins to decrease. [3] [17]
For light nuclei the increase in the specific energy agrees well with the
increase of the specific gravitational energy of the nucleus in the strong
gravitational field, when the energy increases in direct proportion to the
square of mass and in inverse proportion to the radius of the nucleus. The
saturation effect comes into play in the range of 17 to 23 nucleons, forming
the nucleus. Besides, adding a new nucleon to the nucleus increases the energy
not proportionally to the square of mass, but to a lesser extent. This is due
to the fact that gravitons of strong gravitation cannot permeate the nucleus
with a lot of nucleons, as is evident from the exponent. Each new nucleon is
simply pressed to the nucleus from the outside by the strong gravitation, until
for the large nuclei this force reaches the maximum, conditioned by the
pressure of the graviton flux. However, the charged particles of the vacuum in
these conditions have almost 50 times larger path length, and therefore the
positive electrical energy of the nucleus’ protons further decreases the
negative gravitational energy of the nucleus, making the main contribution into
the observed decrease in the specific binding energy of massive nuclei.
, and then begins to decrease. [3] [17]
For light nuclei the increase in the specific energy agrees well with the
increase of the specific gravitational energy of the nucleus in the strong
gravitational field, when the energy increases in direct proportion to the
square of mass and in inverse proportion to the radius of the nucleus. The
saturation effect comes into play in the range of 17 to 23 nucleons, forming
the nucleus. Besides, adding a new nucleon to the nucleus increases the energy
not proportionally to the square of mass, but to a lesser extent. This is due
to the fact that gravitons of strong gravitation cannot permeate the nucleus
with a lot of nucleons, as is evident from the exponent. Each new nucleon is
simply pressed to the nucleus from the outside by the strong gravitation, until
for the large nuclei this force reaches the maximum, conditioned by the
pressure of the graviton flux. However, the charged particles of the vacuum in
these conditions have almost 50 times larger path length, and therefore the
positive electrical energy of the nucleus’ protons further decreases the
negative gravitational energy of the nucleus, making the main contribution into
the observed decrease in the specific binding energy of massive nuclei.
In this model, the fluxes of
charged particles of the vacuum are the cause of the so-called displacement currents in the vacuum, which are proportional to the rate of
change of the electric field with the time. Here, an example is the chargeable
capacitor, between the plates of which there is a magnetic field, despite the
absence of the electron current in the capacitor.
Since the electric constant
remains the same and does not change during SPF symmetry transformation, and the gravitational constant
has its own value at each level of matter, then the electromagnetic interaction
can be considered primary with respect to the gravitational interaction.
Interaction
of the vacuum’s particles with the matter
The main problem of Le Sage’s theory
is the problem of heating of bodies, both for the fluxes of gravitons leading
to gravitation and for the fluxes of charged praons creating electromagnetic
interaction at the nucleon level of matter. Actually, since the fluxes of
gravitons and charged particles must transfer some part of their momentum to
the matter to give rise to gravitational and electromagnetic forces, it also
seems that some part of the energy of these fluxes should turn into the kinetic
energy of motion of the matter and thus heat it to high temperatures, which is
not observed.
It turns out that there is such a
mechanism possible, when the fluxes of smallest relativistic particles transfer
some momentum to the body’s matter, but at the same time they almost completely
conserve their energy and are re-emitted into the surrounding space without
heating the body significantly. So, in physics fields are known that do not
perform work on the particles and do not change their energy. This is the
magnetic field, as well as the gravitational
torsion field in the covariant theory of gravitation, known as the gravitomagnetic field in the general
theory of relativity. A relativistic charged particle, passing through the
region of space with the magnetic field, is deflected from the original
direction of motion by the Lorentz force, in which case the amplitude of the
particle’s momentum and its energy do not change. Despite this, the pressure
force from the particle is exerted on the source of the magnetic field. This
happens because the momentum like any vector can change both in magnitude and
in direction, and any change in the momentum is associated with the
corresponding force.
The analogue of nucleons at the
level of stars is a neutron star, and the fluxes of praons correspond to cosmic
rays. The cosmic rays, passing close to a neutron star, will interact with the
strong magnetic field of the star and be deflected by it. Obviously, if the
flux of cosmic rays on one side of the star is stronger than on the others,
then the stronger flux will start to shift the star due to the magnetic
pressure. The same effect takes place also due to the gravitational torsion
field, which is especially strong in rapidly rotating neutron stars and it
interacts even with neutral fast-moving particles, since it does not act on the
moving charge but on the momentum of particles.
The fluxes of praons moving in
the matter are influenced not only by the magnetic fields of nucleons, but also
by the electric fields of uncompensated charges of individual protons and
electrons. These fields also deflect the fluxes of praons without significant
changes in the energy of praons, which is a consequence of potentiality of the
electric field. Actually, if the fluxes of positively charged praons fly
towards the proton, they are first decelerated by the electric field of the
proton and decrease their energy, and then when they fly past the proton, they
start accelerating from the proton under the influence of the same field and
increase their energy up to the previous level. The gravitational force acts on
the gravitons in a similar way.
With the help of the described
mechanism the fluxes of gravitons and praons can create the gravitational and
electromagnetic interactions in the matter of bodies without heating these
bodies significantly. [5] Passing through the matter the fluxes of
gravitons and praons, consisting of a large number of tiny particles, act
simultaneously on the nucleons, electrons and atomic nuclei, compressing them
in the direction of the gradient of the corresponding flux and creating the
gravitational and electromagnetic acceleration. The fact that the interaction
cross-section ![]() characterizes both the electromagnetic
interaction of the fluxes of praons with nucleons and the strong gravitation
from the fluxes of gravitons at the level of nucleons, and is equal by the
order of magnitude to the cross-section of the nucleon, suggests that the
interaction forces can actually emerge near the surface of nucleons. Here, the
electric and gravitational fields, the magnetic field and the torsion field of
nucleons reach the maximum and can effectively interact with the fluxes of
praons and gravitons. As gravitons, leading to strong gravitation, are
suggested graons as the particles that make up praons just as praons make up
nucleons or as nucleons make up a neutron star. For graons in order to become
gravitons they must be accelerated up to relativistic energies in the processes
near the surface of praons.
characterizes both the electromagnetic
interaction of the fluxes of praons with nucleons and the strong gravitation
from the fluxes of gravitons at the level of nucleons, and is equal by the
order of magnitude to the cross-section of the nucleon, suggests that the
interaction forces can actually emerge near the surface of nucleons. Here, the
electric and gravitational fields, the magnetic field and the torsion field of
nucleons reach the maximum and can effectively interact with the fluxes of
praons and gravitons. As gravitons, leading to strong gravitation, are
suggested graons as the particles that make up praons just as praons make up
nucleons or as nucleons make up a neutron star. For graons in order to become
gravitons they must be accelerated up to relativistic energies in the processes
near the surface of praons.
According to the second problem
of the Le Sage’s theory, during motion excess pressure of gravitons and charged
particles in front should emerge drag effect, proportional to the velocity of the bodies’ motion.
As a result of resistance to the bodies’ motion from the fluxes of gravitons,
long-term rotation of planets around the Sun would not be possible and the
principle of free inertial motion in the absence of forces would not hold true.
When a charged body moves in the fluxes of relativistic charged particles, both
the momentum of the particles falling on the body at the front and the fluence
of the fluxes of these particles increase. This leads to an increase in the
force at the front in proportion to the square of the particles’ energy.
On the other hand, the
cross-section of the praons’ interaction with the matter should be directly
proportional to the square of the de Broglie
wavelength, and inversely proportional to
the square of the energy of praons. This dependence of cross-section in the quantum
theory of elastic scattering is typical of ultrarelativistic photons – the
greater their energy is, the weaker they interact with each other. At the same
time, it is assumed that photons are composed of praons, and the interaction of
praons with the electromagnetic field of nucleons is a special case of photon’s
interaction on virtual photons. Since the force is proportional to the momentum
of the particles, their fluence and the interaction cross section, then the
force remains unchanged both for a fixed and a moving body. Thus, the body can
move by inertia and the decelerating force from the fluxes of charged particles
of the vacuum, proportional to the velocity of motion, does not arise.
The problem of aberration in the
Le Sage’s theory is illustrated by an example, in which in the motion of two
gravitationally bound bodies near each other it seems that in view of the
limited velocity of the gravitons’ motion, a certain additional force takes
place. Indeed, while the gravitons moving from one body reach the second body,
it will move in its orbit from the position that is dictated by the Newton’s
theory of gravitation for instantaneous gravitation. As a result, the gravitons
will reach the second body at some other angle to the orbit, which gives an additional
force component. This problem has been considered for the case, when two bodies
are moving synchronously in the direction perpendicular to the line connecting
the bodies. [1] In this case it was shown that the problem of
aberration of the gravitational force disappears, if we apply the relations of
special theory of relativity to gravitons, which take into account that the
velocity of ultrarelativistic particles is not infinite and is almost equal to
the speed of light. In both cases, for fixed and moving bodies, gravitons reach
these bodies at the same angle with respect to the axes of the proper
coordinate system.
The hypothetical problem of
gravitational shielding in Le Sage’s theory suggests that if we place between
two bodies the third body, it will lead to a more noticeable change in the
forces between the bodies, than in case of the Newton's law of gravitation for
three bodies. The measurements of the possible Moon’s shielding of the Sun’s
gravitational influence on the Earth during Solar eclipses do not find any
deviation from the theory within the limits of measurement error. This
situation is due to the smallness of the cross-section of gravitons’
interaction with the matter. This allows us to expand the exponents in the
expressions for the forces into binomials with sufficiently high accuracy and
ensures the principle of superposition of gravitational forces for several
bodies. A noticeable deviation occurs only for such dense objects as white
dwarfs and especially for neutron stars. A similar situation is obtained for
the case of electromagnetic interaction of bodies by means of charged vacuum
particles, also leading to the principle of superposition.
Emergence
of the relativistic vacuum’s particles
We can distinguish in the vacuum three
components, one of which with the energy density ![]() is associated
with the strong gravitation and the rest energy of particles, determines the
integrity of nucleons and atomic nuclei, and is mainly responsible for the
inertia of bodies. Another component with the energy density
is associated
with the strong gravitation and the rest energy of particles, determines the
integrity of nucleons and atomic nuclei, and is mainly responsible for the
inertia of bodies. Another component with the energy density ![]() is responsible
for the ordinary gravitation, and the third component in the form of charged particles
with the energy density
is responsible
for the ordinary gravitation, and the third component in the form of charged particles
with the energy density ![]() leads to
electromagnetism. Each component makes its own contribution to the mass of
bodies.
leads to
electromagnetism. Each component makes its own contribution to the mass of
bodies.
Based on the principles of
Infinite Hierarchical Nesting of Matter, the densest objects at each level of
matter are assumed as the sources of the relativistic charged particles of
vacuum – neutron stars and magnetars, nucleons and atoms, praons as the
components that make up nucleons, etc. These objects emit neutrinos, photons
and high-energy cosmic rays that can make contribution to the
electrogravitational vacuum at all levels of matter. As a result, the main
sources of vacuum relativistic particles at a certain level of matter are the
emissions from the densest objects at the lower levels of matter. For example,
the core of a neutron star is constantly heated under the action of incident
fluxes of gravitons, having a temperature up to ![]() K. The kinetic
temperature at the surface of neutron stars is determined from observations and
has the typical value of about
K. The kinetic
temperature at the surface of neutron stars is determined from observations and
has the typical value of about ![]() K, and the thermal luminosity rarely exceeds
K, and the thermal luminosity rarely exceeds ![]() J/s. The stellar core is heated enough to
constantly emit neutrino fluxes, escaping from the star and flowing into the
surrounding vacuum. At the time of formation of a neutron star or during its
transformation into a magnetar with reconfiguration of the magnetic moment,
intense neutrino fluxes directed by the magnetic field (due to the connection
between the total magnetic field and the magnetic moments of nucleons) arise,
which will act effectively at a higher level of matter than the stellar level.
J/s. The stellar core is heated enough to
constantly emit neutrino fluxes, escaping from the star and flowing into the
surrounding vacuum. At the time of formation of a neutron star or during its
transformation into a magnetar with reconfiguration of the magnetic moment,
intense neutrino fluxes directed by the magnetic field (due to the connection
between the total magnetic field and the magnetic moments of nucleons) arise,
which will act effectively at a higher level of matter than the stellar level.
Neutron stars generate not only
neutrino fluxes, but also give rise to cosmic rays, as it follows from the
study of supernova remnants. The proton energy on the surface of the charged
magnetar will reach 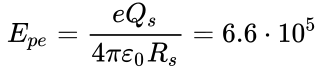 J or
J or ![]() eV, here
eV, here ![]() C is the charge of magnetar,
C is the charge of magnetar, ![]() is the electric constant,
is the electric constant, ![]() km is the star radius.
km is the star radius.
For comparison, the highest
recorded values of cosmic ray energies per 1 nucleon according to estimations
are of the order of ![]() eV, reaching
the Greisen–Zatsepin–Kuzmin limit, and so is the
maximum recorded energy of photons and neutrinos. Oh-My-God particle had
energy of the order of
eV, reaching
the Greisen–Zatsepin–Kuzmin limit, and so is the
maximum recorded energy of photons and neutrinos. Oh-My-God particle had
energy of the order of ![]() eV. If we
assume that the cosmic rays are accelerated from the surface of the discon
surrounding the magnetar, then for the energy of emitted particle with one
elementary charge we can write:
eV. If we
assume that the cosmic rays are accelerated from the surface of the discon
surrounding the magnetar, then for the energy of emitted particle with one
elementary charge we can write: 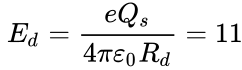 J or
J or ![]() eV, where
eV, where ![]() m denotes the
stellar Bohr radius, while
m denotes the
stellar Bohr radius, while ![]() , where
, where ![]() is the Bohr radius in the hydrogen atom,
is the Bohr radius in the hydrogen atom, ![]() is the coefficient of similarity in size. The
coincidence of energy
is the coefficient of similarity in size. The
coincidence of energy ![]() with the energy of the recorded particles
suggests that the possible source of cosmic rays can actually be magnetars with
discons.
with the energy of the recorded particles
suggests that the possible source of cosmic rays can actually be magnetars with
discons.
In this picture the energy of the
gravitational field is transformed by neutron stars with the help of different
mechanisms into the energy of particles (neutrinos, protons, photons), the high
energy of which causes the high penetrating ability of these particles.
Applying this to other levels of matter, we find the source of the relativistic
particles of vacuum – it is the emissions from the densest objects, such as
nucleons and neutron stars, including the emission of such objects as atoms.
The presence of constant electric charge in the magnetar allows it to generate
cosmic rays and various particles for a long time – similarly to a proton,
which is practically eternal. Thus, if each level of matter would have a long
lifetime, it will be enough to transform the energy of the gravitons at the lower
levels of matter into the energy of charged particles and gravitons, which will
act at the higher levels of matter.
Photons
Main article: Substantial photon model
In substantial electron model the electron in the form of a disk is considered, in
which the charged matter rotates differentially, and ensures the magnetic
moment of the electron. In addition, the electron spin is explained as a result
of shift of the disk’s center relative to the nucleus and rotation of this
center in addition to the matter rotation in the electron cloud. If the
electron transits into the quantum state with lower energy, it emits a photon,
which carries with it the angular momentum that is proportional to the Dirac
constant. In this process, the scattering of charged particles of the vacuum on
the electron disk, taking into account the action of the magnetic and electric
fields in the wave zone, leads to the formation of a photon as an object
preserving its structure for a long time.
In papers, [5] [6]
a model of a photon emitted in an atomic transition in a hydrogen-like atom is
considered. Associating the photon parameters and its structure with the
parameters of the emitter – the charged electron disk, it was possible to
determine the charge to mass ratio for the particles that make up the photon.
As a result, it turned out that photons consist of praons
of very high energies, comparable to the energies that cosmic rays would have
if these rays emerged at the nucleon level of matter near the protons. These
relativistic praons must form the basis of the charged particles of the vacuum,
leading to electromagnetic interaction through the mechanism of Lesage. Indeed,
in the interaction of praons of the vacuum with the electron in atomic
transition, the twisting of praons takes place under action of the fields along
the axis of the electron disk, and the appearing photon carries away the excess
angular momentum of the electron from the atom. Meanwhile, part of praons of
the vacuum is part of the photon, so that the speed of the photon actually is
the speed of praons in the fluxes of particles of the vacuum and close to the
speed of light.
In contrast to the chaotic motion
of praons in the vacuum, the praons in the photon are rigidly bound to each
other by both electromagnetic and gravitational forces. The situation here is
similar to the situation with the nucleons, which only in special circumstances
can form extremely stable formations – the atomic nuclei. According to gravitational model of strong interaction, the nucleons in atomic nuclei are attracted to each
other by strong gravitation and repel each other by means of the gravitational torsion field, arising from the rapid rotation of the nucleons. In
order to form the nucleus, the nucleons must interact with each other only in a
strictly defined orientation of the spins and magnetic moments and must have
sufficient initial energy that allows rotating the nucleons up to the desired
rotation speed by means of gravitational induction.
The praons in the photon can interact with each other in a similar way, and for
the praonic level of matter, the gravitational constant reaches ![]() m3•s–2•kg–1.
In the gravitational field with this large gravitational constant, the praons
of the photon can form sufficiently rigid structure, so that the photon could
fly large cosmic distances without decaying.
m3•s–2•kg–1.
In the gravitational field with this large gravitational constant, the praons
of the photon can form sufficiently rigid structure, so that the photon could
fly large cosmic distances without decaying.
The substantial photon model suggests that photons have the magnetic moment and
the rest mass. Thus, for a photon, emerging in a hydrogen atom when an electron
goes from the second level to the first level in the Lyman series, the
invariant mass of praons that make up the photon is equal to ![]() kg or
kg or ![]() eV/s2 in energy units.
eV/s2 in energy units.
Strong
interaction
According to the gravitational model of strong interaction, strong gravitation acts between the nucleons, holding them together. The
nucleons in the atomic nuclei are attracted to each other due to strong
gravitation and repel each other due to the gravitational torsion field arising from the rapid rotation of nucleons and
leading to spin-spin and spin-momentum forces. In the Lorentz-invariant theory of gravitation the torsion field emerges similarly to the magnetic
field in electromagnetism, and in the general theory of relativity it
corresponds to the gravitomagnetic field. Taking into account that the torsion
field and the gravitational field
strength are the components of the gravitational tensor, strong interaction at the nucleon level of matter is
explained by strong gravitation. At the same time, in contrast to the Standard Model, strong interaction must be acting not only between
hadrons, but also between leptons.
Indeed, in the theory of Infinite Hierarchical Nesting of Matter, elementary particles differ from each other by the
physical state of their matter and consist of praons and praelectrons.
Similarly, the matter of the objects at the stellar level of matter (the matter
of planets, main sequence stars and other ordinary stars, white dwarfs and
neutron stars) consists of nucleons and electrons in different phase states.
Strong gravitation actually acts on every praon of an
elementary particle regardless of the type of this particle, just as ordinary
gravitation at the Earth’s surface acts either on individual nucleons or on the
same nucleons as part of a test body with any state of matter.
At each basic level of matter there
is its own gravitation, which is characterized by its own gravitational
constant, and there is also electromagnetic interaction between the charges.
Since gravitational and electromagnetic interactions can be explained by the
action of relativistic particles of the electrogravitational vacuum, then
strong interaction at each level of matter turns out to be a consequence of the
corresponding gravitational interaction, and not a substantially different type
of interaction. In particular, it is assumed that strong gravitation and hence
strong interaction at the nucleon level of matter are caused by the action of
the fluxes of relativistic graons present in the electrogravitational vacuum
and acting on the matter of elementary particles. [5]
Weak
interaction
The role of weak interaction reduces to the fact that under the action of the
fundamental forces and the strong interaction of objects after their formation
take place a slow transformation of matter. For example, a neutron in a very
large time by the standards of atomic processes turns into a proton, an
electron and a neutrino. The transformation of the matter can be significantly
accelerated by external factors. Thus, the incident on an elementary particle a
neutrino can easily convert the matter of the particle and cause it to decay
into other particles.
In the substantial neutron model, the free neutron decay is analyzed using a stellar
model in the form of a neutron star. It is concluded that slow transformation
of the stellar matter occurs due to the cooling of the star and the subsequent
beta decays of the matter’s neutrons. The neutron beta decay is a consequence
of the fact that individual neutral praons in the neutron’s matter undergo
their own beta decays and turn into positively charged praons, praelectrons and
antineutrinos of the praon level of matter. All this leads to the fact that
after a great number of such decays positively charged praons and negatively
charged praelectrons are accumulated in the neutron shell. When the magnetic
field from the charged praons exceeds the magnetic field from the neutral
praons, a catastrophic reconfiguration of the total magnetic field occurs in
the neutron with ejection of the negatively charged part of the shell. Thus, a
neutron becomes a proton and emits an electron and an electron antineutrino. In
fact, this antineutrino represents the sum of praneutrinos and praantineutrinos
emitted by a set of praons of the neutron’s matter in the course of the neutron
decay.
It follows from the above that
the processes of weak interaction at a certain basic level of matter again are
reduced to the processes of weak interaction, but already at a lower level of
matter. At the same time, the role of relativistic particles of the
electrogravitational vacuum at all levels of matter is reduced to the dynamic
action on the matter’s particles, which we consider as gravitational and
electromagnetic interactions, and at the level of nucleons it is represented as
strong interaction. The fact that the long-term dynamic action of the vacuum’s
particles on objects finally can lead to a rapid transformation of their matter
and to emission of the particles like neutrinos and antineutrinos is perceived
by us as a manifestation of weak interaction. This also includes reverse
processes, when neutrinos and antineutrinos themselves interact with various
objects and transform their matter with subsequent decay.
Neutrinos
According to the picture of weak
interaction in the model of electrogravitational vacuum, neutrinos and
antineutrinos, similarly to photons, are the vacuum’s particles. On the other
hand, neutrinos and antineutrinos themselves must consist of the main objects
of the respective levels of matter. In particular, it is assumed that neutrinos
and antineutrinos of the nucleon level of matter consist of graons, in contrast
to photons, which consist of praons. [5]
Indeed, during the neutron beta
decay an electron antineutrino is emitted, which consists of the fluxes of
electron praneutrinos and praantineutrinos resulting from the beta decays of
praons of the nucleon’s matter. In the course of the beta decay of each praon,
only graons and even smaller particles of the lower levels of matter can become
part of the emerging praneutrino or praantineutrino.
The analysis carried out in the
book [3] shows that the electron antineutrino has the right-handed
helicity and is emitted mainly in the direction of the spin of the decaying
neutron. This means that the fluxes of electron praneutrinos and
praantineutrinos, forming an electron antineutrino, are twisted to the right.
If the same fluxes in other decays are twisted to the left, then an electron
neutrino emerges. Between rotating praneutrinos and praantineutrinos,
consisting of graons, there is strong gravitation at the matter level of graons, which holds them
together as part of neutrinos or antineutrinos and ensures their long-term
stability.
Muon neutrinos and antineutrinos
emerge from the decay of charged pions into muons, as well as from the decay of
muons into an electron (positron) and an electron antineutrino (neutrino),
depending on the sign of the muon charge. In particular, if the magnetic moment
of the positive pion coincides in direction with its rotation, then when the
pion decays, a muon neutrino, having the left-handed helicity, should be
emitted mainly in the direction of the south pole of the magnetic field and
against the pion spin, with the helicity corresponding in direction to the
rotation of the pion’s matter.
Similarly to electron neutrinos,
a muon neutrino consists of polarized fluxes of electron praneutrinos and
praantineutrinos, resulting from the weak interaction reactions in the matter
of decaying particles. The difference between electron and muon neutrinos is
mainly associated with the difference in their energy and the peculiarities of
those objects that emit these neutrinos. It is due to the similar composition
of their constituent parts that electron and muon neutrinos have the ability to
transform into each other in neutrino oscillations.
Cosmology
In the observable universe, the following properties are found:
- Up to the largest
distances, the space practically represents the flat Euclidean space,
which can be seen from the dependence of the angular sizes of the most
extended extragalactic radio sources on the redshift.
- The observable universe on a large scale is
approximately uniform and isotropic, and therefore it can be considered as
a relativistic uniform system.
- The ratio of the concentration of cosmic
microwave background radiation
400-500 photons/cm3 to the average concentration of nucleons in
the observable universe is proportional to the specific entropy of cosmic
space and can reach the value of the order of
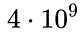 .
. - The baryon
asymmetry of the
universe, manifested as the predominance of baryons over antibaryons.
The above-mentioned properties of
the observable universe should be explained in every cosmological theory. For
example, the most distant regions of the observable universe are so far from
each other that during the estimated time of its existence they would not be
able to interact with each other and to achieve the state of uniformity and
isotropy. The processes of interaction between particles and wave quanta in the
course of evolution of the observable universe must be such as to lead to the
observed ratio of photons to nucleons.
According to the Lambda-CDM model, in the visible Universe concentration of baryons is
of the order ![]() nucleons per cubic meter. From the ratio
nucleons per cubic meter. From the ratio ![]() at a given concentration of nucleons and the
known value of the cross section for the interaction of gravitons with matter
for ordinary gravitation
at a given concentration of nucleons and the
known value of the cross section for the interaction of gravitons with matter
for ordinary gravitation ![]() m2
it is possible to estimate the free path length of gravitons:
m2
it is possible to estimate the free path length of gravitons: ![]() m. This value is 23 orders of magnitude
greater than the visible size of the Universe, which is estimated by the value
of 14 billion parsecs or
m. This value is 23 orders of magnitude
greater than the visible size of the Universe, which is estimated by the value
of 14 billion parsecs or ![]() m.
m.
Similarly may be estimated the
length of free path of the charged particles of the vacuum in the cosmic space,
taking as the charge concentration in a first approximation the value ![]() of the elementary charge per
cubic meter, which is equal to the average concentration of baryons in the
Universe. This approach gives only the minimum value of the free path length,
since on the average the matter in the Universe is neutral, and
of the elementary charge per
cubic meter, which is equal to the average concentration of baryons in the
Universe. This approach gives only the minimum value of the free path length,
since on the average the matter in the Universe is neutral, and ![]() must reflects the average concentration of
the total charge of the Universe. From the ratio
must reflects the average concentration of
the total charge of the Universe. From the ratio ![]() at a given concentration of charges and the value
at a given concentration of charges and the value ![]() m2,
the free path length of charged particles is
m2,
the free path length of charged particles is ![]() m. This value
is 3 orders of magnitude greater than the visible size of the Universe.
Consequently, the charged particles and gravitons can easily reach our Universe
from a distance.
m. This value
is 3 orders of magnitude greater than the visible size of the Universe.
Consequently, the charged particles and gravitons can easily reach our Universe
from a distance.
From the standpoint of similarity
of matter levels, the set of all stars in the visible Universe corresponds to
extremely rarefied atomic gas. At first glance, this rarefied gas of stars,
even in view of the lower levels of matter, cannot create this energy density
of the graviton field ![]() J/m3. But in remote areas of cosmic space
the density of matter can be much greater and reach such values, that it can
generate the necessary energy density of the graviton field, reaching our
Universe.
J/m3. But in remote areas of cosmic space
the density of matter can be much greater and reach such values, that it can
generate the necessary energy density of the graviton field, reaching our
Universe.
The effects of redshift of the
galaxy spectra and the attenuation of emission from distant supernovae can be
explained by the fact that the light is scattered on new particles or nuons. [18]
These particles are neutral particles of muon type, which emerged naturally in
the same way as white dwarfs emerge in the course of stellar evolution. The
sizes of nuons and their concentration in space, according to Infinite
Hierarchical Nesting of Matter, are so just such that can explain the
scattering of light. Nuons also explain the appearance of background emission
and the effects attributed to dark matter. If we admit the existence of nuons,
then the most important arguments in favor of the Big bang model become
useless. If the Universe has existed longer than 13.8 billion years, then
gravitons could have got into our Universe from outside and carried out their
action here.
This shows that 61% of all praons
are part of nucleons, and the rest 39% form nuons or exist separately. The same
proportion remains at the level of stars: 61% of all nucleons over time will be
part of neutron stars, and the rest of nucleons remain either as a gas or as
the matter of white dwarfs. Consequently, the concentration of free protons in
the visible Universe must be of the same order as the averaged over the entire
space concentration of nucleons in stars, that is of the order of concentration
of baryons ![]() m–3, according to the Lambda-Cold
Dark Model. With this in mind, the product of the concentration of baryons and
the binding energy of a neutron star in the calculation per nucleon will give
us the estimate of the maximum energy density of emission in cosmic space:
m–3, according to the Lambda-Cold
Dark Model. With this in mind, the product of the concentration of baryons and
the binding energy of a neutron star in the calculation per nucleon will give
us the estimate of the maximum energy density of emission in cosmic space: ![]() J/m3.
Indeed, the energy density in the relic radiation equals
J/m3.
Indeed, the energy density in the relic radiation equals ![]() J/m 3,
and the energy density in the stellar radiation, magnetic fields and cosmic
rays is of the same order of magnitude, as well as the kinetic energy of the
motion of gas particles. The sum of these energy densities does not exceed the
maximum energy density
J/m 3,
and the energy density in the stellar radiation, magnetic fields and cosmic
rays is of the same order of magnitude, as well as the kinetic energy of the
motion of gas particles. The sum of these energy densities does not exceed the
maximum energy density ![]() .
.
Thus, the electrogravitational
vacuum of the universe, filled with the same particles regardless of the
observation point, due to the unified scheme of evolution of the matter’s
particles at different levels of matter, allows us to explain the uniformity
and entropy of photons in the observable universe. In this case, the
predominance of baryons over antibaryons, which seems surprising in the hot Big
Bang model, can occur due to the significant difference in probabilities of
emergence of particles and antiparticles in the model of cold and long-term
evolution of the universe. As for the observed flatness of space, it is a
consequence of the low mass density of the observable universe.
Extended
special theory of relativity
At each point of the
electrogravitational vacuum, such isotropic reference frame can be chosen that
in it, on the average, the same and mutually opposite fluxes of vacuum
particles would pass through any unit area per unit time. Thus, there will be
no initially selected direction of motion of these particles. In an isotropic
reference frame, the speed of light is the same in all directions. In the extended special theory of relativity (ESTR), the contradictory in its essence postulate
about the constancy of the speed of light and its independence from the motion
of light sources and from the motion of the observer is replaced by a
physically more understandable postulate about the existence of an isotropic
reference frame. This leads to the fact that all relations of the special relativity can
be derived in new axiomatics. As a result, the constancy of the speed of light
in inertial reference frames is derived as one of the consequences of ESTR.
General
field
The electrogravitational vacuum
manifests itself by the fact that the neutral and charged particles present in
it, when acting on the bodies’ matter, lead to gravitational and
electromagnetic forces between these bodies. These forces ensure both the
integrity of bodies and the observed hierarchy of matter levels. In addition,
the corresponding charge and mass, as a measure of inertia, can be attributed
to each body. The standard description of the electromagnetic field is its
representation in the form of the vector four-dimensional field with the
electromagnetic four-potential ![]() . A similar approach for gravitation gives the
vector covariant theory of gravitation, defined with the help of the gravitational four-potential
. A similar approach for gravitation gives the
vector covariant theory of gravitation, defined with the help of the gravitational four-potential ![]() . In addition to the electromagnetic and
gravitational fields, other fields can be detected in the matter of macroscopic
bodies, for example, the pressure field, the dissipation field, and
the acceleration field. The
four-potentials
. In addition to the electromagnetic and
gravitational fields, other fields can be detected in the matter of macroscopic
bodies, for example, the pressure field, the dissipation field, and
the acceleration field. The
four-potentials ![]() ,
, ![]() and
and ![]() can be attributed to these fields,
respectively, and these fields can be considered as vector fields. [19]
[20]
can be attributed to these fields,
respectively, and these fields can be considered as vector fields. [19]
[20]
In contrast to a scalar field, a
vector field takes into account the dependence of the four-potential on the
velocity of the field source’s motion, and therefore it provides a more
accurate description of reality. As a result, all vector fields are either
direct or indirect consequences of the action of the electrogravitational
vacuum’s particles on the matter, and we can assume that there is a certain
general field, which has, as its basis, a single source associated with the
vacuum. [21] To emphasize the relative independence of gravitational
and the electromagnetic field, the general field was divided into two main
components. [22] One of them is the mass component of the general
field, the source of which is the mass four-current ![]() . The source of the second one – the charge
component of the general field – is the charge four-current
. The source of the second one – the charge
component of the general field – is the charge four-current ![]() . The mass component of the general field
contains the gravitational field, acceleration field, pressure field,
dissipation field, fields of strong and weak interaction, and other vector
fields. The charge component of the general field represents the
electromagnetic field. The four-potential of the charge component of the
general field is the electromagnetic four-potential
. The mass component of the general field
contains the gravitational field, acceleration field, pressure field,
dissipation field, fields of strong and weak interaction, and other vector
fields. The charge component of the general field represents the
electromagnetic field. The four-potential of the charge component of the
general field is the electromagnetic four-potential ![]() . The four-potential of the mass
component of the general field is equal to the sum of the four-potentials of
the corresponding fields:
. The four-potential of the mass
component of the general field is equal to the sum of the four-potentials of
the corresponding fields:
![]()
where the four-potentials ![]() and
and ![]() describe the fields of strong and weak
interactions in macroscopic bodies, and the effects associated with these
fields.
describe the fields of strong and weak
interactions in macroscopic bodies, and the effects associated with these
fields.
In view of its definition, none
of the general field’s components can have the energy density that would exceed
the field mass-energy
limit as the energy density of the
corresponding component of the electrogravitational vacuum.
Preferred reference frames
Mach's
principle is closely related to the assertion about
possibility of existence of a preferred (privileged) reference frame defined by
any objects of the Universe. It is assumed that the change in the motion of any
body relative to the preferred reference frame caused by the action of another
body leads to an inertia force acting from the side of the first body to the
second and changing its state of motion. So, inertial mass is detected in each
body, the product of which on acceleration of the body is equal to the force of
inertia.
The following
statements are known that describe the preferred reference frame:
- Newton: A preferred reference frame is associated
with absolute space and time.
- Mach: A preferred reference frame is associated
with the distribution of matter in the Universe.
- Einstein: According to the theory of relativity,
there is no preferred reference frame, or it does not appear and therefore
is not required in the formulation of the theory.
- Fedosin (based on the
modernized Le Sage’s theory, extended
special theory of relativity, Lorentz-invariant theory of gravitation): The preferred reference frames can be
determined by those reference frames in which at the moment fluxes of
gravitons in the electrogravitational vacuum are spatially isotropic.
Fluxes of
gravitons, arriving at an arbitrary point in space, depend on remote sources of
gravitons, and therefore cannot always be exactly the same from all sides, even
taking into account the averaging of the action of a huge number of such
sources. Following the fluctuations of the graviton fluxes, an isotropic
reference frame at a given point must change its velocity in order to be
considered isotropic. As a result, isotropic reference frames at different
points in space can have different velocities relative to each other. This
means that in the general case there is no single preferred reference frame for
the entire space of the Universe and therefore there is no absolute
simultaneity of events.
However, the
averaging procedure allows us to move from microscopically set values to their
average values at the macro level that characterize the system as a whole. It
is known that on a scale of more than 100 Mpc, our Universe looks like a
uniform system. When averaging at such scales, we can talk about a certain
global preferred reference frame, which is isotropic in the first
approximation. With the same degree of approximation in such frame of
reference, the absolute simultaneity of events occurring on a scale of more
than 100 Mpc is achieved. In all other cases, we can only have the relative
simultaneity of events.
Cosmic microwave background radiation can be considered
as one of the components of the electrogravitational vacuum. The inhomogeneity
and a high degree of isotropy of the CMB coming to the Earth make it possible
to accurately determine the preferred reference frame associated with this
radiation. This reference frame moves relative to the Sun at a speed of the
order of 370 km/s in the direction opposite to the direction to the
constellation Leo.
A global
preferred reference frame, defined by the supposed single dynamic medium of
reference, was introduced in an article written by Olivier Pignard. [23]
The indicated
dynamic medium affects the surrounding bodies in approximately the same way as
the action of graviton fluxes of the electrogravitational vacuum, leading to
the effect of gravitation. The following features of the dynamic medium are
postulated:
1. This medium
is a medium for propagation of light.
2. The speed
of light varies near massive bodies.
3. Bodies
affect the dynamic medium so that it manifests itself in the form of a
curvature of space-time of the general theory of relativity. This means that
test particles and photons accordingly change their motion near massive bodies.
4. Near the
bodies fluxes of the given medium arise towards the center of these bodies. The
speed and acceleration of such a flux are given by the formulas:

where ![]() is the gravitational constant,
is the gravitational constant, ![]() is the body mass,
is the body mass, ![]() is the distance from the center of the body to
the point of observation outside the body.
is the distance from the center of the body to
the point of observation outside the body.
The velocity ![]() of the dynamic medium flux affects the rulers
and clocks that are stationary relative to the massive body in the same way as
if these rulers and clocks moved in the inertial reference frame with the same
velocity
of the dynamic medium flux affects the rulers
and clocks that are stationary relative to the massive body in the same way as
if these rulers and clocks moved in the inertial reference frame with the same
velocity ![]() in the absence of the massive body. This
means that in both cases, the same relativistic effects appear that reduce the
size of the rulers and slow down the time of the clock, regardless of whether
the flux of the dynamic medium moves relative to the rulers and the clock, or
the rulers and the clock themselves move relative to the dynamic medium. In
particular, relativistic effects due to movement at a speed
in the absence of the massive body. This
means that in both cases, the same relativistic effects appear that reduce the
size of the rulers and slow down the time of the clock, regardless of whether
the flux of the dynamic medium moves relative to the rulers and the clock, or
the rulers and the clock themselves move relative to the dynamic medium. In
particular, relativistic effects due to movement at a speed ![]() of a certain reference frame in an inertial
reference frame depend on the Lorentz factor
of a certain reference frame in an inertial
reference frame depend on the Lorentz factor
 . If we put
. If we put ![]() , then instead of the Lorentz factor in
general relativity, the equivalent value
, then instead of the Lorentz factor in
general relativity, the equivalent value  appears.
appears.
The above
features of the dynamic medium are in complete agreement with the properties of
electrogravitational vacuum, in which photons are formed from relativistic
vacuum particles and therefore move almost at the speed of light, just like
gravitons. In the Lesage model, the graviton flux incident on a body from a
certain direction always exceeds the oncoming graviton flux passing through the
body from the opposite direction due to the interaction of gravitons with
matter and their partial scattering and absorption. This just corresponds to
the fact that there arises a total flux of gravitons, which can be modeled as
some centripetal directed graviton flux falling from the outside onto any body
with the
velocity ![]() .
.
The flux of a
dynamic medium considered above can be considered as the total flux of
gravitons acting on rulers and clocks and leading to relativistic effects of length contraction and time
dilation depending on the relative speed of the rulers and clocks in the
isotropic reference frame. In this case, the special theory of relativity
usually considers the movement of rulers and clocks in inertial frames of
reference moving with an arbitrary constant speed relative to a globally isotropic
frame of reference with slightly massive bodies that weakly affect graviton
fluxes. If the bodies are massive, it is necessary to take into account the
general relativity and distortion of the fluxes of gravitons near such bodies.
In this case, we can assume that the velocities of numerous isotropic reference
frames are directed towards massive bodies. Although the rulers and the clock
may be stationary relative to a body, they will be in motion relative to the
local isotropic reference frame at the location of the rulers and the clock.
This leads to relativistic effects in the gravitational field.
As for the
relativistic effect of changing the speed of light near massive bodies, it is
closely related to the procedure of spatio-temporal measurements by means of
light in a light clock, when the bi-directional motion of the light signal
along a closed path is taken into account. This effect appears for a coordinate
observer, that is, for a remote external observer in an inertial reference
frame that is stationary relative to the body, while for a local observer
located at the point of measurement of the speed of light, the speed of light
does not change.
At the same
time, the light source in the light clock should not generate a single narrow
beam, but a sufficiently wide light front so that at least part of this front
reaches the reflector and returns back to the receiver located next to the
light source. Indeed, the relative motion of the measuring system in an
isotropic reference frame can lead to a deviation of a narrow light beam from
the direction of the moving reflector and to signal loss in the receiver.
A change in
the speed of light near massive bodies should be considered as an apparent
effect, similar to the apparent (not real) reduction in body size in the
direction of its movement. Other apparent effects include a length contraction in the
gravitational field for the coordinate observer and transformation of the
moving sphere into a Heaviside ellipsoid according to the special theory of relativity.
In the model of electrogravitational vacuum, ordinary photons are formed
from fluxes of relativistic praons under the action of strong fields near
elementary particles. In this case, the speed of the photons should be less
than the speed of motion of the praons, since the photons not only move in a
straight line, but also rotate. Upon transition to the underlying level of
matter of graons, it becomes clear that the speeds of relativistic graons are
higher than the speeds of praons, and photons consisting of graons move faster
than ordinary photons, as can be seen from the increase in the Lorentz factor.
The speeds of all these particles do not exceed the speed of light. In particular, if ![]() is Lorentz factor of a relativistic particle,
then the speed of this particle is
is Lorentz factor of a relativistic particle,
then the speed of this particle is 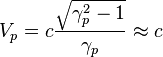 .
It turns out that the speed of light is the limit value for the speed of
motion of relativistic vacuum particles, including photons at all levels of
matter. In this sense, the speed of light becomes a fundamental quantity. Based
on the fact that gravitational waves are waves of graviton fluxes in the form
of praons, and photons are composed of praons and move slower than praons, the
propagation speed of the gravitational signal can slightly exceed the speed of
the electromagnetic signal.
.
It turns out that the speed of light is the limit value for the speed of
motion of relativistic vacuum particles, including photons at all levels of
matter. In this sense, the speed of light becomes a fundamental quantity. Based
on the fact that gravitational waves are waves of graviton fluxes in the form
of praons, and photons are composed of praons and move slower than praons, the
propagation speed of the gravitational signal can slightly exceed the speed of
the electromagnetic signal.
References
- 1.0 1.1 1.2 Fedosin S.G. Model
of Gravitational Interaction in the Concept of Gravitons. Journal of
Vectorial Relativity, Vol. 4, No. 1, pp. 1-24 (2009). http://dx.doi.org/10.5281/zenodo.890886.
- 2.0 2.1 2.2 2.3
Fedosin S.G. The graviton field as the source of mass and gravitational
force in the modernized Le Sage’s model. Physical Science International
Journal, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
- 3.0 3.1 3.2 3.3 3.4
3.5 Sergey Fedosin. The physical theories and infinite
hierarchical nesting of matter, Volume
1, LAP LAMBERT Academic Publishing, pages: 580, ISBN-13:
978-3-659-57301-9. (2014).
- ↑Fedosin S.G. The Force Vacuum Field as an Alternative to the
Ether and Quantum Vacuum. WSEAS
Transactions on Applied and Theoretical Mechanics, ISSN / E-ISSN:
1991‒8747 / 2224‒3429, Volume 10, Art. #3, pp. 31-38 (2015). http://dx.doi.org/10.5281/zenodo.888979.
- 5.0 5.1 5.2 5.3
5.4 5.5 5.6 Fedosin S.G. The charged component of the vacuum field as
the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences,
Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357.
- 6.0 6.1 6.2 Fedosin S.G. The substantial model of the photon. Journal of Fundamental and Applied Sciences,
Vol. 9, No. 1, pp. 411-467 (2017). http://dx.doi.org/10.4314/jfas.v9i1.25.
- Fedosin S.G. On the structure of the force field in electro gravitational vacuum. Canadian Journal of Pure and Applied Sciences, Vol. 15, No. 1, pp. 5125-5131 (2021). http://doi.org/10.5281/zenodo.4515206.
- Fedosin S.G. Energy and metric gauging in the
covariant theory of gravitation. Aksaray University Journal of Science and
Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.
- Wang Zhongxiang,
Chakrabarty Deepto, Kaplan David L. A Debris
Disk Around An Isolated Young Neutron Star. Nature, Volume 440, pages
772–775 (2006). arXiv: astro-ph / 0604076 v1.
- Ü. Ertan et al. On the Evolution of Anomalous
X-ray Pulsars and Soft Gamma-ray Repeaters with Fall Back Disks. ApJ, Vol.
702, pp. 1309 (2009). https://dx.doi.org/10.1088/0004-637X/702/2/1309.
- Fedosin S.G. The Gravitational Field in the
Relativistic Uniform Model within the Framework of the Covariant Theory of
Gravitation. International Letters of Chemistry, Physics and Astronomy,
Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.
- 11.0 11.1 11.2 Fedosin S.G.
(1999), written at Perm, pages 544, Fizika i filosofiia podobiia ot preonov do metagalaktik, ISBN 5-8131-0012-1.
- Fedosin S.G. The radius
of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363
(2012). http://dx.doi.org/10.5281/zenodo.889451.
- Fedosin S.G. The binding energy and the total
energy of a macroscopic body in the relativistic uniform model. Middle
East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
- Fedosin S.G. The Mass Hierarchy in the
Relativistic Uniform System. Bulletin of Pure and Applied Sciences,
Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.
- Fedosin S.G. The
Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the
Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No.
4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12.
- Fedosin S.G. The
Principle of Proportionality of Mass and Energy: New Version. Caspian Journal of Applied Sciences Research,
Vol. 1, No 13, pp. 1-15 (2012). http://dx.doi.org/10.5281/zenodo.890753.
- Fedosin S.G. Cosmic Red
Shift, Microwave Background, and New Particles. Galilean Electrodynamics, Vol. 23, Special
Issues No. 1, pp. 3-13 (2012). http://dx.doi.org/10.5281/zenodo.890806.
- Fedosin S.G. The
procedure of finding the stress-energy tensor and vector field equations
of any form. Advanced
Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101.
- Fedosin S.G. Four-Dimensional Equation of Motion
for Viscous Compressible and Charged Fluid with Regard to the Acceleration
Field, Pressure Field and Dissipation Field. International Journal of
Thermodynamics. Vol. 18, No. 1, pp. 13‒24 (2015). http://dx.doi.org/10.5541/ijot.5000034003..
- Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016),
e2459. http://dx.doi.org/10.4236/oalib.1102459.
- Fedosin S.G. Two components of the macroscopic
general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2,
1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025.
- Pignard O. Dynamic medium
of reference: A new theory of gravitation. Physics Essays, Vol.
32(4), pp. 422-438 (2019). http://dx.doi.org/10.4006/0836-1398-32.4.422.
See
also
External links
Source:
http://sergf.ru/even.htm