Galilean Electrodynamics, Spring 2012, Vol. 23,
Special Issues No. 1, P. 3 – 13.
Cosmic Red Shift, Microwave
Background, and New Particles
Sergey G.
Fedosin
Perm State University, Russia
Abstract
The
explanation of the red shift in spectra of remote galaxies and cosmic microwave
background radiation from the concept of an expanding Universe seems
inadequate, and invites other explanations.
The present paper studies the idea of cosmic red shift and microwave
background radiation as a consequence of interaction between photons and
previously unknown particles. It shows
that the overall mass of the new particles in the Universe has the same order
of magnitude as the mass of all the nucleons.
Thus the problem of invisible dark matter may be solved. The question must be raised about the need
for the existence of dark energy. In
particular, the effect of attenuation of radiation from the distant supernovas
is considered to be the consequence of scattering of photons on the new
particles, but not the result of the dark energy activity.
Key Words: Red
shift; Cosmic Microwave Background Radiation (CMBR); Particles; Dark matter;
PACS: 14.80.-j ; 95.30 C ; 95.35 ; 98.70.Vc
1. Introduction
The cosmological
red shift of wavelengths observable in spectra of remote galaxies, and the
almost isotropic CMBR with a spectrum close to the radiation of a black body,
were the major discoveries of the last century.
The usual interpretation of the red shift is reduced to the appearance
of the Doppler effect as a consequence of the expansion of space throughout the
Universe, together with all the contents.
In this case the further from us the galaxy is, the more its speed 
should be. So it is supposed that the red shift confirms
the theory of the Big Bang, which could generate our Universe.
Accordingly, the
CMBR that existed in the early hot and dense Universe is considered to have
cooled by the present time. Thus the
radiation temperature should fall in inverse proportion to the distance scale factor, and the energy density must
fall in inverse proportion to the fourth power of the scale factor. However, the given explanations collide with
many difficulties that exist in the model of the expanding Universe.
First of all, we
would like to note the insufficiency from a philosophical point of view of the
explanation of the red shift effects and the CMBR as the consequence of space
expansion. Really, according to the
theory some initial and extremely dense substance is supposed to exist, and in
the result of its transformation, substance, radiation and space start to
expand. The idea of space expansion is
necessary for the stationarity of the Universe, which has finite substance
density, and for the explanation of the fact that the more remote galaxies have
greater red shift. The unsatisfactory
aspect of this theory is the assumption of the existence of the primary matter
with surprising properties, arising from nowhere, and not less surprising scale
factor of a geometrical-mathematical nature which leads to the space expansion
in a set way [1].
The high degree
of the temperature isotropy of the CMBR coming from different parts of the sky
means that there is a certain connection between the properties of remote
galaxies. But these galaxies could not
cooperate with each other during the presumable age of the Universe because of the
large distance between them. Therefore,
into the theory the idea of an inflationary phase is introduced, assuming
extremely high rates of expansion of the early Universe.
In connection
with these and many other problems, the questions of any actual substantiation
of cosmological theories were repeatedly considered. So, in [2] are analyzed the consequences
arising from the idea of the red shift, not as the result of the Doppler
effect, but rather of the interaction in space with particles of the type of
axions, or 
-particles. It is
possible to consider our work as continuation of movement in this
direction. We also offer a description
of the connection between the red shift and the CMBR.
2. Red Shift
If we consider
the red shift of this or that galaxy as the result of its movement, then
according to the relativistic Doppler effect there is a change of wavelength 
of the electromagnetic
signal coming from the given galaxy to the Earth:
, (1)
where 
is the angle between
the velocity vector of the galaxy and
the direction to the Earth, 
is the speed of light,
and 
is the wavelength
observable on the Earth.
At large
distances, the angle is close to 
for galaxies
scattering from each other; therefore, it is possible to put 
. It then follows from
(1) that the red shift 
, understood as a relative change of the wavelength, looks
like:
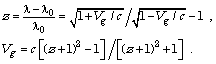(2)
At small , the dependence of the galaxy speed in (2) becomes a very a
simple formula:
. (3)
At the same
time, Hubble's empirical law connects the distance to the galaxy, determined by
independent methods, with the red shift of its spectrum:
, (4)
where 
km/(s·Mpc) is Hubble's
parameter.
The expression
for the probable speed of galaxies depending on the distance to them follows
from equations (3) and (4): 
.
We consider,
that the red shift of galaxies’ spectra is not connected
with any moving apart of the galaxies, but rather with the effect of reduction
of photon energy in their propagation through space. From the common viewpoint, the photon
can be considered as an oscillator that should reduce its energy with
time. If the angular wave frequency of a
photon is 
, and the energy of the photon is 
, then the 
-factor of the photon as an oscillator is determined in this
way:
. (5)
Supposing the -factor is time-independent, by integration of (5) we come to
the following dependence of the photon energy on time:
. (6)
Let us assume
further, that the -factor is directly proportional to the angular frequency of
the photon, and the time is proportional to the distance 
passed by the
photon. As 
, where 
is Planck's constant,
and 
is the frequency of
the wave, it is possible to rewrite (6) as:
, 
, (7)
where 
is a constant, and 
are the wavelength and
frequency of the photon wave at its radiation.
From (7) it
turns out that as the photon propagates and the distance passed increases, the
length of the photon wave grows. Taking
into account (7) and the definition of the red shift , we shall obtain:
. (8)
The combination
of equations (4) and (8) allows us to find parameter 
. At small value of
the red shift, it is possible to simplify (8), expanding the exponent, further
using in (4), we find and also 
:
, 
, 
. (9)
The parameter is the distance on
which the photon energy decreases in 
2.718 times (
is the basis of the
natural logarithm), range of is determined by the
discrepancy of measurements of Hubble parameter.
3. Model of a Photon
In order to
speak in more detail about energy losses in electromagnetic quanta during their
propagation in cosmological space, we shall consider an elementary model of a
photon [3]. The given model has been
constructed by the analysis of movement of the test charged particles in the
field of an electromagnetic wave. Then
by means of inverse transformation, the similar self-coordinated movement of
particles forms a wave. In this case we
consider that this wave is circularly polarized, and the wave’s particles
support the form of the photon.
If the wave in
the photon is directed along the 
axis, then the
centripetal force acting in the plane 
is necessary for
particles to move on a helical line. The
equation of the movement of the wave particle is determined by Lorentz's force
through which the acceleration 
can be found:
, (10)
here 
is the mass of the
particle, 
is the charge of the
particle, 
is the vector of the
wave’s electric field intensity, 
is the vector of
magnetic field induction, 
is the particle
velocity vector.
As the plane of
polarization of the wave rotates along the axis, for the
component of fields, in view of perpendicularity and , it is possible to write:
, 
, 
,
(11)
, 
.
Using conditions
(11) in (10) and considering, that 
, we shall obtain the equations for speeds:
, (12)
(13)
(14)
Expressing 
from (13) and 
from (14), and using
them in (12), we come to an equation that can be integrated:
(15)
where 
is a constant of
integration.
The speeds of
particles of the following kind are the solutions of the equations (13) and (14),
in view of conditions (11) for intensities of electric field:
, 
, (16)
and
the following equations are carried out:
, 
. (17)
Using speeds
(16) in (15), we find the speed of particles along the axis:
. (18)
For each speed
amplitude 
, the speed of photon particles 
along the direction of
its propagation can be equal to speed of light by the choice of a constant in (18).
Thus, the photon
can be presented in the form of helical structure in which the charged
particles rotate along the direction of photon’s movement. To keep particles from scattering, it is
necessary to add centripetal force. It
can be the gravitational force operating from the bunch of particles, which
make a photon in aggregate. Besides, it
is possible to consider the Lorentz force from the longitudinal magnetic field 
also created by
particles. For example, fast movement of
charged particles is equivalent to current, attracted
to each other under action of magnetic forces.
Because of the
fact that the equations of the gravitational field are very similar to
Maxwell’s equations for an electromagnetic field [4,5], both fields have been
incorporated in a unified electro-gravitational field. Therefore, the carriers of both fields, a
photon and a graviton, can make a single whole.
In particular, the photon can be imagined as gravitons transferring also
electromagnetic energy.
4. Mechanism of Energy Loss by
Photons
It is possible to
approach dependence (7) in a different way, by specification of the way of
energy loss by photons. It is easy to
notice, that expression (7) is very similar to the law of absorption of energy
of radiation in the substance, known as the law of Bouguer-Lambert-Beer. For the case when radiation passes through
the rarefied medium, for example in gas clouds in space, reduction of light
intensity in a gas layer with thickness occurs by exponent and
is described by the formula:
, (19)
where 
is the initial light
intensity, 
is the effective
cross-section of light dispersion, and 
is the concentration
of disseminating particles.
With the help of
(19), knowing the thickness of the gas cloud and effective cross-section of
light dispersion (which usually corresponds to the size of gas atoms), it is
possible to estimate the concentration of atoms in the cloud.
Our idea about
cosmological red shift is that (19) is true not only for the total light
intensity from many photons, but also for each separate photon. Really, in the space such small particles can
exist, meeting with which the energy of a photon will slightly decrease. The model of a photon described above,
includes the coordinated movement of a set of particles so meeting with
extraneous particles the photon will lose
energy. At the same time the change of
photon’s energy will be accompanied also by the change of length of photon’s
wave – that is effect of red shift.
From (7), (9)
and (19) it follows, that it should be in the following way:
, (20)
where is the length of mean
free path of photons among the particles disseminating them.
To estimate from
(20) sizes of disseminating particles through their section , in the beginning it is necessary to determine the
concentration of these particles in the space. It is preliminarily possible to assume, that
the given particles have the sizes much less than atomic so they do not reveal
themselves directly.
5. Similarity of Nuclear and Star
Systems
In the given
part we shall try to estimate the average concentration of particles in the
space, on the basis of the theory of similarity and the principle of embedding
of matter levels in each other [19]. The
theory of similarity already has some conclusions that are exact enough. For example, the value of the minimal mass of
stars 
has been predicted in
[3]. Stars of such masses have been
really discovered, and are known as brown L-dwarfs and T- dwarfs.
It is easy to
assume that at each level of matter there are such objects that possess the
largest densities of mass and energy. We
consider that at the level of stars the densest objects are neutron stars,
instead of the hypothetical black holes.
This follows from the fact that when the set of particles is combined in
one body there is always emptiness between the particles leading to reduction
of the body’s density in relation to the density of one particle.
A black hole has
properties such that in density of energy it corresponds to nucleons. If we assume the existence of black holes,
that means it is necessary to assume the presence of gravitational forces,
significant in power, that are able to pull the substance together in a black
hole. However, the particles of
gravitational field, gravitons, do not exist separately and are not given from
the outside; they are a product generated by the matter. Stars, for example, generate radiation,
substance streams and cosmic rays. Due
to the law of conservation of energy, any radiation from a body cannot be more
energetic than the full energy of this body.
Therefore with
transition to a higher-scale level of matter, the effective density of energy
of field particles and the largest possible density of object’s substance
decrease simultaneously.
If it were not
so, at each level of matter there would be black holes. As it is known from the theory, black holes
should possess ability completely to absorb matter and even radiation, giving
back only small part of energy. As
evolution proceeds more quickly at the lowest scale levels of matter, it is
necessary to expect there the fuller transformation of substance into black
holes, up to the full exhaustion of free substance. But then the opportunity for formation of the
energetic particles making a field at higher levels of matter disappears as the activity of black holes for this purpose
becomes insufficient. From this
contradiction only one conclusion can be drawn: there are not objects of the
black holes type at each level of matter.
This is the same as the existence of completely absolute objects also
being not admitted in philosophy.
Supposing, that
at the level of elementary particles, the densest objects are nucleons, and at
the level of stars – neutron stars, so based on the recent data [20] we shall
make Table 1 to determine the coefficients of their similarity.
Table
1. Parameters and Coefficients of
Similarity
for Neutron
Stars and Nucleons
|
Mass, kg |
Radius, m |
Characteristic speed,
m/s |
|
Neutron star |
||
|
|
|
|
|
Proton |
||
|
|
|
|
|
Coefficients of
similarity |
||
|
|
|
|
From Table 1 it
follows, that a neutron star contains the quantity of nucleons equal to 
on the
average. The typical speed of particles 
for a neutron star has
been calculated from equality of the value 
and the full energy of
the star including gravitational and internal thermal energy. A similar equality
is available for a proton – for that, 
in Einstein's
equation also is equal to the full energy.
The coefficient of similarity by the sizes is determined by the formula:
.
Let us assume
now, that the nucleon also contains 
the particles called
‘praons’. Such a conclusion follows from
the fact proved in [6] based on huge actual material: the existence of a ladder
of space objects from praons up to meta-galaxies for which relations of
similarity are carried out.
We have a
question now: what is the density of substance of praons, average for all
space? To determine this it is necessary
to find the coefficient of similarity 
by the density between
levels of matter of nucleons and praons.
The density of substance is measured in kg/m3. Therefore according to the theory of
similarity it is necessary to divide coefficient of similarity in mass by a
cube of coefficient of similarity in the sizes:
.
Now it is
possible to estimate the average density of substance of praons 
in the Universe
through the average density of mass of nucleons 
from here:
, (21)
where 
and 
are from Table 1.
The result (21)
can be understood from following reasoning.
At the level of stars part of nucleons is concentrated in neutron stars with
density of substance 
, other nucleons are concentrated in substance of common
stars, in the dust and in space gas. The
relation of density to the average density
of nucleons in the Universe is equal 
. The same proportion
can be written down for the level of elementary particles: 
, where 
– density of substance of a proton. From 
in view of 
the equality (21) just
follows.
The part of
praons obviously is contained in nucleons, but from (21) it is evident, that the
density of praons’ mass as a whole exceeds density of nucleons’ mass that we
observe in the Universe. As 
, the difference of densities is equal 
. It turns out, that
there is also substance of praons, distributed in space with average density 
. The share of nucleon
substance is 100/1.64 = 61 % of all mass, and 39 % of mass exists in some other
form.
Long ago
indications have already been made that there is the invisible substance in
space called dark matter. Observable curve rotations of clusters of
stars and galaxies near each other in many cases differ from what can be
expected in case of presence of only nucleon substance. Such difference is attributed to gravitational
influence of the dark matter.
Based on the
star evolution theory the following distribution of stars according to the
condition of their substance is predicted.
In the present time in our Galaxy there are about 
stars, most of
which are on the main sequence. In the
interior of these stars nuclear reactions actively proceed similar to the
Sun. The white dwarfs, dense and cooling
down kernels of stars of the main sequence, make up to 10% of all stars of the
Galaxy. Such kernels remain after
burning out of kernel fuel in stars and the subsequent dropping of the external
envelope by the stars. Neutron stars in
the Galaxy can be up to 
if we consider their
increased frequency of occurrence in the past and consider them as the basic
source of observed quantity of heavy metals. In future transformation of all stars
of the main sequence either in white dwarfs or in neutron stars is
expected.
Masses of white
dwarfs do not exceed masses of neutron stars, as white dwarfs drop actively
superfluous substance in flashes of novae stars. The cases of formation of neutron stars from
white dwarfs are not excluded; as it is very well possible if their critical
mass is exceeded. For white dwarfs, the
mass and the radius are inversely related, as the most massive of them have the
smallest radii. The substance density of
even the most massive white dwarfs is a million times less than the density of
neutron stars. Therefore, in the course
of evolution of the set of stars and white dwarfs, after their accumulation in
the center of the Galaxy, they will be broken off because of gravitational
forces from the nearest neutron stars.
Nevertheless, it is possible to assume that a significant part of white
dwarfs will remain on the periphery and outside the galaxies.
If we now go to
the level of elementary particles of matter, it is necessary to expect that,
besides nucleons in the rarefied space, there should also be so-called ‘newons’ (new particles),
with properties similar to those of white dwarfs. Then the set of these particles forms the
dark matter. The given particles should
be millions of times less dense than nucleons.
As the sizes of white dwarfs are hundreds and thousands of times greater
than the sizes of neutron stars, the same is to be expected for the new
particles in relation to the sizes of nucleons.
The average
density of baryonic substance in the Meta-galaxy estimated up to 
kg/m3
according to [21], with the concentration of baryons of about 0.26 per m3.
As we consider that
the share of nucleon matter accounts for 61% of the total mass, and 39% of the
mass consists of new particles with masses somewhat smaller than the nucleon
mass, then the estimated concentration of new particles gives the value up to 
/m3. Using now the concentration given in (20) with
Hubble's parameter 
km/(s·Mpc), it is
possible to estimate the cross section of the scattering
particles and their characteristic size 
:
(22)
Multiplying the
size of new particles by
the coefficient of similarity for the sizes 
from Table 1, we
receive the value of about 
m that is
close to the range of radii of white dwarfs.
Thus, the new
particles, which are similar to white dwarfs in their properties, can really be
scattering particles, and effectively reduce the energy of photons in their
distribution in the space.
It is easy to
estimate that the scattering of the new particles against each other or on
nucleons should occur very rarely. At
the temperature of about 10 K, the speed of particles with the mass of a
nucleon is 
m/s. Then the average time between collisions will
be about 
years, where 
Gpc according to
(20).
If the effect of
red shift is caused by interaction of photons with new particles, then as the
consequence of different average concentration of new particles in the way of
photons, the red shift can be different in different directions in the sky. Such an effect is really observed, leading to
a different Hubble parameter (by almost twice) received by the researchers who
study different parts of the sky. Even
the adjacent parts of the sky, on one of which there is a significant emptiness
in distribution of close galaxies, can give a difference in measured values of
Hubble’s parameter.
6. Red Shift and Meta-Galaxy
Nowadays,
quasars with the value more than 6 are
discovered. For example, the object HCM
6A has red shift 
[7]. Using (7) and parameter from (9), and Hubble's
parameter of 
km/(s·Mpc), we receive
the distance to HCM 6A equal to 7.76 Gpc.
It is known that according to observations, the majority of quasars are
at the distances corresponding to red shifts from 
up to 
; at 
their quantity sharply
decreases [8]. Our estimation for gives distance 1.05
Gpc = 
light years, and for – distance 4.39 Gpc,
or 13.5
109 light years.
If we suppose
that in their development all large galaxies in the Meta-Galaxy have somehow
come through ‘the quasars phase’, which is characterized by strengthened
generation of energy, then it is possible to assume that the given phase began
in the Meta-galaxy approximately 
years ago (at ). Considering that
quasars on the whole finish their active phase
at the time of their observation 
years (), we can estimate the time of quasars’ existence and the
active phase of the Meta-galaxy at 
years. The given condition concerns not only
quasars, but also galaxies with the large luminosity of other types, for
example to ultra-luminescent infra-red galaxies ULIRG, the largest of which do
not almost meet at 
[9]. Gamma-ray
bursts also basically are found out up to [18].
According to the
data described in [10], periodicity of red shifts in radiation from galaxies in
clusters is observed. After translating
these 
in speed by means of
(3), we find characteristic differences in speed 
with values from 2.67
km/s up to 72 km/s. For relative red
shifts for components in pair
galaxies, the values 
up to 20 km/s, and up
to 220 km/s in clusters of galaxies, has been found.
In [11] were
found repeating speeds with values of 24.2
km/s, 36.3 km/s and 72.5 km/s for the group of 89 nearest spiral galaxies,
especially at 37.2 km/s for one subgroup from 40 galaxies.
From Eq. (2)
connecting red shift of a galaxy and its speed, it follows that galaxies should
have inexplicable quantization in speeds if we treat the observable
quantization of red shift as the consequence of Doppler effect. If we consider that cosmological red shift
depends on the length of the path that is passed by light, from (8) and (9) it
follows, that the periodicity of red shift is connected with the periodicity of
distance under the formula:
. (23)
It is evident
that at small distances to galaxies and small the exponent makes
small contribution and the periodicity of differences in distances in
considered galaxies follows from the periodicity of differences in red shifts
in groups of galaxies. At large
distances and red shifts the periodicity is not clear, as in (23) the exponent
makes the significant contribution, and different will correspond to
similar 
. This last fact also
results from research of red shifts of quasars and galaxies most of which are
far from us. However, the periodicity
should be restored, if in each separate measurement and red shift will be used
in (23). In the result such basic
periodicity must appear which
would correspond to the characteristic distance between separate quasars or
galaxies.
Based on (23),
Table 2 gives us an interpretation of
periodicity of the red shifts that were described in [10]
and [11], and were expressed there in the form of periodicity of speed .
Table
2. Periodicity of red shifts
|
|
|
Interpretation |
|
2.67 |
0.03 |
The size of
large galaxies, the minimal radius of the circulation of satellites around
them – dwarfish galaxies |
|
20 – 24.2 |
0.22 – 0.27 |
The radius of
gravitational influence of a large galaxy, measured by the maximal orbits of
its satellites – dwarfish galaxies (an example – our Galaxy) |
|
36.3 – 37.2 |
0.40 – 0.415 |
The distance
between the adjacent large galaxies |
|
72 – 72.5 |
0.8 |
The separation
of galaxies in the clusters, the double distance between the adjacent large
galaxies |
|
220 |
2.45 |
The size of
clusters of galaxies |
|
12000 |
140 |
The average
size of galaxies’ super-cluster in the Meta-galaxy in view of the emptiness between
super-clusters |
We can notice
that in Table 2 the values of (and accordingly of ) differ from each other approximately by an integer
multiplier, which gives a cause for additional connection to take place between
separate observable periodicities of the red shift . In the last line of
Table 2, we have added the periodicity connected with super-clusters of
galaxies (
light years), discovered, including, on the basis of statistical
researches of dependence of luminosity of luminescent red galaxies on the
distance.
The accuracy of
measurement of red shift now reaches the value of 
, which is equivalent according to (3) to the accuracy of
measurement of speed up to 1 km/s.
Therefore the red shift is well observed already in radius 1.5 – 2 Mpc
of the dwarfish galaxies that surround the connected pair, consisting of our
Galaxy and the next galaxy, Andromeda.
At these distances, so-called ‘Hubble flow’ appears where it is required
to consider red shift [12]. But it seems
absolutely unreal that all these nearest dwarfish galaxies could simultaneously
move away from us because of the Universe’s expansion. And how does one
explain that within a very non-uniform distribution of matter in the Local
volume with the radius of 20 Mpc, it caused regular flow of cosmological
expansion with linear velocity dependence on the distance? Why do local and global flows of expansion
have the same dependence? And since the
talk is about expanding the entire Universe with all its contents, then we need
to recognize expansion of galaxies and stars and the Earth itself?
At the same
time, if the red shift is not the result of Doppler effect, but of interaction
of photons with new particles, the dwarfish galaxies remain turning peacefully
around the large galaxies.
In [13], the
regular rotation of the polarization plane of the electromagnetic radiation
propagating on cosmological distances has been found. The result is proportional to the distance to
the source of radiation, and does not depend on usual Faraday effect, which is
subtracted from the obtained data. The
characteristic spatial scale for the discovered effect makes the value of about 
m, that is less than from (9). It is not excluded that
this rotation of the polarization plane, as well as red shift, that, also is
due to interaction of radiation with new particles. Really, new particles like white dwarfs can
have the magnetic moments and be guided by intergalactic magnetic fields. This allows regular influence of particles on
the plane of polarization.
7.
Dark Matter
As
was shown above, up to 39 % of all mass in the Universe can be in the form of
new particles, and the share of nucleons is 61%
of the mass. Such situation allows one
to explain the observable discrepancy between the distribution of visible mass
in star and galactic clusters and the rotation of these masses near each
other. The majority of nucleons in
galaxies are inside of stars. The new
particles are unlikely to be inside of stars, as at large substance density they
will break up in collisions with much denser nucleons. Therefore, new particles are extensively
accumulated in the space surrounding galaxies, and considerably exceed the
visible borders of galaxies.
Speeds of
rotation of small bodies outside a massive body can be derived from the
condition of equality of gravitational and centripetal accelerations:
, from which 
, (24)
where 
is the gravitational
constant, 
is the mass of
substance inside of the radius 
.
It is evident
that the speed should decrease with increase in distance from the center of a
galaxy. However, it is very frequent
even at large distances from galaxies that almost constant speed of rotation
can be observed. For example, in our
Galaxy the average speed of stars’ rotation is about 250 km/s; it begins with
the distance of about 8 kpc, and proceeds at least up to 20 kpc. That is possible, if we consider that the
mass in (24) in the range from 8 up to 20 kpc accrues linearly with radius, and
the average substance density falls down in inverse proportion to a square of
radius. Therefore the mass of the Galaxy
within the limits of radius 20 kpc should be about 
, where 
is the mass of the
Sun. Our Sun is not further than 10 kpc
from the center of the Galaxy.
Estimations of substance density show that, already in the solar neighborhood,
up to half of the mass of all galactic substance should fall to the dark
matter.
The question of
existence of dark matter is especially acute in clusters of galaxies, for some
of which the full energy of visible substance is close to zero, or seems even
to be positive. Then according to the
movement dynamics of masses in a gravitational field, dissociation of such
clusters should be expected. In order to
prevent that, it is necessary to introduce the dark matter for an increase of
the module of potential gravitation energy having on the whole a negative
sign. At the scales of clusters and
super-clusters, the relative quantity of dark matter is required to be even
more than in galaxies. It is considered
that on the scales of clusters of galaxies, the invisible substance should not
be less than five times more than the visible.
For example, in
the cluster of galaxies Coma, the number of galaxies in volume 1 Mpc3
makes about 40, which means that the average distance between the galaxies
equals 29 kpc. And the relation of mass
of the cluster to the general luminosity, in terms of mass and luminosity of
the Sun, reaches 250, whereas for a separate galaxy, such a relation does not
exceed 50. If the nucleons are mostly
within cluster of galaxies and dark matter in the whole volume of the cluster,
then the total mass of new particles may be sufficient for the observed lack of
substance.
All space
objects known to us from asteroids to galaxies have a round form. It is rather mysterious, that the clusters of
galaxies basically bi-dimensional, and the super-clusters of galaxies are more
close to fibers, than to round objects.
The length of super-clusters can be in range 10 – 100 Mpc, the
cross-section up to 75 Mpc, the relation of length to width can reach 5. Super-clusters are usually directed to each
other by the ends of their large axes, and in knots and branches of fibers of
super-clusters, the largest clusters of galaxies are located.
It is obvious
that such a form of matter on large scales is the consequence of a reduction of
average substance density in large objects.
Really, a cell of uniformity of substance in the Meta-galaxy presumably
is about 140 Mpc. It is possible to
consider that in view of emptiness, this is the size of one super-cluster on
average in the Meta-galaxy. The average
substance densities of the close cells almost do not differ from each other,
and the basic gravitational forces not only the result of the ordinary matter,
but also distributed in the space of dark matter. This is the reason why super-clusters do not
interact actively, not with their neighbors, and not even with their own
internal parts. Instead of round-form
objects, the super-clusters form fibers – they are extended in length due to
interaction with the close and massive neighbors in those places, where the
attraction is strong enough.
Let us add some
more remarks concerning the characteristics of the Meta-galaxy, the Universe on the whole.
The standard approach is connected with consideration of the Universe on
the basis of the general relativity theory.
Within the limits of accepted idealizations, it is considered that the
parameter of gravitation is constant.
According to this fact, the substance of
the infinite Universe cannot be static only in the presence of gravitational
forces, and therefore in view of the red shift effect it can extend. And it happens so, that the further from us
the observed objects are, the more the expansion speed is. Evolution of the Universe in this case is
determined by the average density of the substance mass and the mass-energy of
all available fields.
However we
consider that the red shift is not the consequence of the Universe’s
expansion. It becomes appropriate to
raise the question about applicability of that idealization due to which the
invariability of gravitational forces and of the gravitational constant in all
spatial scales is supposed, including even the Universe. Since gravitation cannot be a force given to
the whole Universe from the outside, it should be created within the Universe,
as the consequence of the microscopic levels of the matter. But we know that, for example, the nuclear
forces binding the substance of nucleons, cease to work on large distances. It will be more natural to consider, therefore,
that gravitational forces have a finite range of action. Let us add to it that probably there is more
or less an empty space outside the Meta-galaxy up to other meta-galaxies. Continuing further, such distribution of
substance, we come to the fact that the average density of the Universe tends
to zero at infinity. That can be an
additional reason that it is necessary to explain the organization of the
Universe not just with the help of general relativity theory; other physical
constructions should also be involved.
Instead of
trying to apply gravitation theory to the whole Universe at once, we shall try
to specify the possible parameters of our Meta-galaxy. The evolution of the Meta-galaxy can proceed
not by means of explosion, but in a quieter manner, by gradual gravitational
aggregation of substance from an originally more homogeneous condition. For such a case, the estimation of the
maximal age of the Meta-galaxy can be calculated from the time of gravitational
falling of substance:
years.
Then the
estimation obtained above of ‘the quasar stage’ in development of the
Meta-galaxy, which begun years ago and ended 
years ago, means, that
only after the long process of aggregation of substance right up to the size of
large galaxies, the most active phase of the Meta-galaxy begins and it
continues on the whole years. Besides, according to estimates of energy
release, this or that quasar or a galaxy can themselves be hyper-active only in
the range of not more than 
years; then they pass
in the category of less active galaxies.
Let us accept,
as an extreme case, that the gravitational potential of the Meta-galaxy reaches
10% from the maximum value, equal to the square of the light speed. Then from the relation: 
it is possible to
estimate the radius of the Meta-galaxy
from the known average substance density 
kg/m3. For we find the value 6.9
Gpc. With such a size, the Meta-galaxy
remains Euclidean to within 10%, and it can be described in the classical
way. It can possibly be true that the
farthest of observable objects (the distance to them according to (8) can be up
to 9.6 Gpc at 
) are now already outside the Meta-galaxy, or the gravitation
ceases to work at such large distances.
Then the necessity for obligatory use of the general relativity theory
for the whole Universe can disappear by itself.
Here we can add
that the Euclidean nature of space up to very large distances can possibly be
proved by means of angular measurements of the sizes of extragalactic objects
depending on the distance to them.
8. Apparent
Stellar
Magnitudes
By definition,
the apparent stellar magnitude is:
, (25)
where ‘
’ is logarithm to the base 10, 
is the flow of
radiation of the object, is the distance in
parsecs from the object to the observer, and 
is a constant.
In order to
consider the dependence of the observed star magnitude on the red shift, it is
necessary to express from (8) and to use
the result in (25). Besides, the emitted
light reduces its energy according to (6) and (7). One more effect is connected with scattering
of photons on new particles, owing to which photons may change their direction
in space. This leads to effective
reduction of quantity of the photons received on the Earth during observation.
As a first
approximation, this effect can be considered by means of multiplication in (25) by 
, where 
is some
coefficient. Having made the necessary
replacements, we shall obtain:
where ‘
’ is logarithm to the base .
If we arrange
the radiating object on distance of 10 pc, then instead of 
there will be the
absolute magnitude of the object:
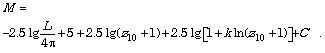
As the red shift
at a distance of 10 pc
is very small, it can be ignored.
Further by means of subtraction of expression from it is possible to get
rid of some parameters:
(26)
where – parameter from (9).
Because of the
red shift from remote supernovae of type Ia, which were invoked in a number of works
as standard sources of powerful radiation with known luminosity and duration of
bright luminescence of tens days, there were difficulties in interpretation of
the obtained results. In [14] supernovae
were compared with red shifts from 0.3 up to 0.62 to the similar supernovae
near us. By the amplitude of the light
curve and its change in the course of time, it is possible to estimate absolute
star magnitude and other parameters, including the distance to supernovae. It is accepted that, owing to the specific
character of its formation from white dwarfs, the energy of supernovae of type
Ia depends little on the place and the time of the flash. As a result, it appears that at the moment of
the flash, all the given supernovae should seem to be further than what follows
from Hubble's law with 
km/(s·Mpc), approximately, by 10 to 15%.
The authors of
[14] find the explanation that the expansion of the Universe occurs under
action of some additional factor, except for gravitation. Such factor is considered to be the vacuum
(or dark) energy connected with the cosmological constant, included in
Einstein-Hilbert's equation for the metrics as a parameter. Unlike the density of the matter energy, the
density of the vacuum energy is supposed to be a constant, irrespective of the
Universe’s expansion. The given
assumption (about creation of vacuum energy), is obviously, not less fantastic,
than geometrical expansion of the Universe.
Under action of dark energy the scale factor of expansion in the past
becomes relatively more, which can increase the distance to supernovae at the
moment of radiation up to the necessary value because of what the radiation
flow from them becomes weaker.
Our approach
does not demand relativity theory, the concept of space expansion, and
invocation of dark energy for the explanation of discrepancy in distances of
supernovae, as is done in [14]. We consider
that the given effect can be explained as the consequence of scattering of
photons on the way to the Earth and corresponding reduction of their
quantity. According to [14] and [15],
the average magnitudes 
for different red
shifts of supernovae are these: 
for 
, 
for 
, 
for 
. This means that, as
the red shift increases and remoteness of supernovae grows, the apparent magnitude
becomes more positive, showing reduction of radiation flow.
Using the data 
and in (26), we receive
the estimate of 
. The discrepancy in arises from the
approximate nature of our assumption that the stream of energy from a supernova
decreases in inverse proportion to the distance in the form of 
. It is obvious
that the law of scattering of photons should be replaced with another, more
exact expression. However it is clear
that the reduction of the quantity of photons due to their scattering by new
particles can fully explain the lack of energy that is found out in remote
supernovae. As the factor of the order of unity,
it is evident that the effect of scattering of photons is additional to the red
shift effect. Both these effects are the
consequence of interaction of photons with new particles.
9.
Cosmic Microwave Background
Radiation (CMBR)
The effective
temperature of an isotropic CMBR corresponds to the temperature of a black body
about 2.725 ± 0.001 K. The average
energy density is 
J/m3, the
wavelength of the maximum in the spectrum of radiation energy is about 1
mm. The accuracy of measurement of
temperature in the adjacent spatial areas now reaches 
. It is possible to
discover the existing temperature heterogeneity up to 
from the average.
In order to
connect the CMBR with the new particles, we shall consider distribution of
light in the environment. Let be the initial
intensity of light, 
– the intensity of
reflected light, 
– the intensity of
delivered light, 
– the intensity of absorbed
light in a layer with thickness . These intensities
are connected among themselves:
.
In the case of
infinite cosmological space, the light is repeatedly reflected and
absorbed. Similarly to (7), the for
intensity of light after passing the distance in the environment we
have:
, and also 
. (27)
In (27) it is
possible to consider that 
at 
(reflection and
absorption in a layer of zero thickness do not exist). With very large , all reflected and absorbed radiation finally will be
thermalized by new particles, and will acquire the spectrum of a black body, so
according to (27) it should be true that 
where 
is the radiating ability of absolutely black body at
temperature 
.
Thus, radiation
received on the Earth from remote sources of electromagnetic radiation should
contain a component that has the spectrum of a
black body. What can the temperature of
this black body be?
From what is
stated, it is evident that it should be 
. Hence, the energy
density of CMBR should have the same value as the energy density of other
electromagnetic radiation. This is
really observed, so a spherical particle placed far from stars gets on the
average the temperature of about several Kelvin units due to radiation from
stars. Hence, the temperature 2.7 K of
the black body consisting of disseminating particles is the average temperature
of new particles. As it has been shown
above, the concentration of new particles in space exceeds the concentration of
nucleons, and the radii of new particles are hundreds of times more than the
radii of nucleons.
Another possible
source of CMBR is connected with the interaction of new particles with
surrounding substance. It is more
convenient to consider in the beginning the interaction of white dwarfs, as
direct analogues of new particles, with the substance surrounding these
stars. It is known, that most of the
stars are connected in star pairs. Close
double pairs with white dwarfs very often give strong flashes, which are the
consequence of substance flow to the white dwarf from the star-partner and the
subsequent explosion. The energy of
flashes get to the range 
– 
J for nova-like stars
NL, 
J for repeated novae Nr, 
J for novae stars
N. We shall translate now these energies
into corresponding energies of new particles, for this we should divide the
energy in view of data of Table 1 by the coefficient of similarity in energy 
. As a result we
receive energies in a range 
J, with a maximum close to the lowest magnitude just
corresponding to the energy of photons of the CMBR. Thus new particles, collecting the smallest
substance around themselves, owing to their properties could also generate CMBR
themselves.
Exact
measurements of temperature of CMBR in different directions in the sky show
that the CMBR comes from very large distances.
The CMBR likely comes from outside of the Meta-galaxy, from distances,
which are much large than 1 Gpc. If we
take into account that the energy of photons drops with distance, then the
whole curve of the CMBR can be shifted entirely to the direction of the increase
of the wavelength.
Between the
arrangement of galaxies’ clusters and temperature points of the CMBR, there are
weak correlations connected with interaction of photons and the substance of
galaxies. On the other hand, the sizes
of space objects have some spectrum that should be reflected in measurements of
temperature difference 
of the CMBR between
neighboring points, made with change of the angle of the sky overview. The less the angle of the overview is, the
less the sky area at each measurement of temperature is. If the angular sizes of the effective sources
(or scatterers) of the CMBR coincide with the angle of the overview of the
tools for measurement of temperature difference, small peaks of should be
expected. Similar peaks are observed in
the decomposition of the power spectrum of CMBR into angular harmonics 
, where 
is the effective angle
of the sky overview [16]. In the concept
of an expanding Universe, such peaks are interpreted as the consequence of the
oscillatory heterogeneities, which could have been in the dense substance of
the small Universe in the distant past.
From our point
of view, the peaks are the evidence of the different degree of heterogeneity of
substance distribution existing in the Universe up to the present time. Let us assume that in the parts of space
visible to us, there exist objects with the maximal size, such as
super-clusters of galaxies. Further, as
the size reduces, clusters of galaxies and galaxies themselves will
follow. With homogeneous distribution of
these objects, we should expect that the nearest super-clusters will on the
average be located at the certain distance 
from us, and will be
visible under the average angle of the overview 
. At distances less
than , we shall see only clusters of galaxies with average
distance from us 
, and the average angle of overview 
. The increase of the
angle of the overview to more than will not give resonance, because we assume, for example, that
super-clusters of galaxies are the largest objects. If 
, 
for the angular
harmonics, and the size of the Meta-galaxy is of
order 
Gpc, then the average size of galaxies’ super-cluster will be equal to
Mpc.
This value is close to the size of cell uniformity in Meta-galaxy
substances in Table 2. All subsequent
peaks with 
in the decomposition
of the spectrum have declining angular
scales , which correspond to all the
smaller objects, from clusters of galaxies, just before galaxies. Besides, the CMBR at very large
distances simply cannot reach us because of lessening of the photons’
energy. Thus, we consider that the
reason for occurrence of peaks in the energy spectrum of CMBR is the presence
of substance heterogeneities in the Meta-galaxy and in its nearest environment,
irrespective of the concept of the expanding Universe.
10.
Luminosity of Matter in a
Meta-Galaxy
By means of (7)
it is possible to estimate the average rate of generation of electromagnetic
energy in a unit volume in space. We
shall designate this function as ; its units are W/m3. We shall place the all-wave energy receiver
at the origin of our coordinate system, putting it in the plane ZOX for measuring the arriving
energy. If the radiating volume is at
distance from the origin of the
coordinate system, the effective quantity of energy which falls in the unit of time to the unit
area of the receiver, 
, will be
, (28)
where 
are the spherical
coordinates of the radiating volume 
.
The exponent in
(28) reduces the energy of all electromagnetic quanta upon their passing the
distance according to (7) and
(9). The multiplier in (28)
reflects the reduction of the quantity of arriving photons due to their
dispersion at different angles on new particles, [see text near Eq.
(26)].
Integrating (28),
we obtain the energy flow 
coming from a spatial
hemisphere of infinite radius to the unit area of the receiver:
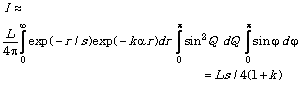, (29)
where according
to (9) 
.
Measuring the
power of the energy falling on the receiver, it is possible with the known
value 
Gpc and , to estimate from (29) the characteristic power of electromagnetic
energy developed in the unit volume of the Universe, . This can vary in different
directions, reflecting the variability of Hubble parameter and substance
distribution in space.
11.
Evolution
of Elementary Particles
In the above
part about the similarity of nuclear and star systems, it was said that new
particles, as well as nucleons, are the product of development of the Universe,
similar to white dwarfs and neutron stars.
In this picture, it turns out that both stars and elementary particles
have appeared from the substance that was getting more condensed during
evolution. The processes of aggregation
and accumulation of the substance can occur synchronously in very large volumes
of space, as is observed in our Meta-galaxy, providing their relative
homogeneity and isotropy.
There is a
question: can we find new particles on the Earth if we assume their
considerable amount in space and even their prevalence over nucleons? What place is occupied by new particles among
known elementary particles?
The analysis of
similarity relations between particles in [3] gives the following
information. It is known that hadrons
include baryons and mesons. The lightest
baryon is the nucleon, and the lightest meson – the pion. All hadrons, except for nucleons, are
unstable and disintegrate in the course of time. From the point of view of similarity, a
neutron star with mass 
(this mass in 6.8
times less than the mass of a neutron star in Table 1) corresponds to a pion,
as it is lighter than a nucleon by 6.8 times.
However, the substance of neutron stars with such small mass is unstable
[17], and therefore such stars should disintegrate. We shall assume that, in the course of time, a neutron star with mass will
disintegrate to form a hydrogen cloud with mass of the order of mass of the
star. This process would be equivalent to
the reaction of decay of a pion to a muon and muonic neutrino (antineutrino):
.
Further, as a
muon is 8.89 times lighter than a nucleon, a hydrogen star corresponding a muon
has the mass 
. Decay of a muon to
an electron (or positron) and electronic and muonic neutrino take place
according to reaction:
.
By means of the
data in Table 1 it is possible to estimate the lifetime of neutron stars with
small mass – the analogs of pions.
Multiplying the lifetime of the charged pions 
s by the coefficient of time similarity 
, we obtain:
years.
For this time in
a neutron star of small mass, we should expect a transformation of substance
that would entail its transformation to a star object of large size. The lifetime of muons is 100 times more than
pion’s lifetime; therefore, for the corresponding stars, the lifetime will be
about 
years. As a first
approximation, it is possible to assume that for the given time there occurs a
compression of the hydrogen cloud. As a
result of the compression in the star, thermonuclear reactions begin, and it
becomes a star of the main sequence. Thus
to the process of radiation of electron and neutrino at disintegration of muon
there corresponds emission of the envelop of such star and corresponding
radiation. Subsequently the star turns
in a helium white dwarf.
In the described
picture, hadrons are similar to neutron stars in unstable, stable, or excited
conditions. The latter basically
concerns the particles-resonances, which by their very short lifetimes
correspond to the massive, very hot and unstable neutron stars.
We classify new
particles as leptons of muons’ type, which at the level of stars correspond to
white dwarfs. However we find difference
between the leptons obtained on the Earth in experiments on collision of
particles, and the new particles that have appeared in the space during natural
evolution. This difference results from
different ways of formation of muons and new particles – if muons are formed
because of disintegration of pions, new particles are formed in the inverse
process of aggregation and condensation of substance. Similarly, white dwarfs, being the remains of
disintegration of low mass neutron stars, should have strong magnetic fields
and should differ from those white dwarfs which appeared from the stars of the
main sequence in the course of standard star evolution. If we assume that new particles are not only
stable, but also neutral, it will be extremely difficult to discover them with
the existing methods.
12.
Conclusions
So, we explain
the red shift by loss of energy in light quanta in their propagation in space,
and the periodicity of the red shift –by approximately identical distances
between the adjacent measured objects, repeating again and again in different
clusters of galaxies. It is obvious that
the explanation of the periodicity of red shifts within the limits of the
concept of the expanding Universe is complicated. Really, for two galaxies moving close to each
other, the red shift cannot be significantly different as they do not scatter
from each other, but they are the components of a pair. At the same time, it is observed on a large
scale, with characteristic periodicity of the relative red shift in pairs of
galaxies. Precisely the same periodicity
is shown, not only in interacting close pairs, but also in an arrangement of
galaxies in clusters along the line of sight, as the consequence of their
approximately identical space separation.
The occurrence
of the two cosmological effects – the red shift and the CMBR – in our opinion occurs
due to the action of the uniform space substratum consisting of new
particles. The existence of new
particles follows from the unified scenario of formation of space objects, from
micro-particles up to galaxies, which is based on aggregation of substance and the
subsequent scattering of high-energy particles.
The electromagnetic energy of the Universe dissipates on new particles,
which leads to red shift of the wavelength of photons, and at the same time it
is transformed into background blackbody radiation. The other source of CMBR is supposed to be
the radiation from the new particles themselves, which is connected with their
interaction with the substance of the environment.
The new
particles allow us to approach the questions
of existence of the dark matter and to the dark energy itself in a different
way. Owing to their weak observability,
the new particles can make the basis for dark matter. At the same time, it is possible to deny the
necessity of introduction of dark energy, explaining the effects attributed to
it with the action of new particles.
We find the
reason for homogeneity of CMBR in homogeneity of distribution of new particles
in the Universe. At the same time,
homogeneity of all the remaining substance, and of the electromagnetic
radiation connected with it, is also observed on a large scale in the
Universe. The specified homogeneities
are the consequence of formation and evolution of both the new particles, and
all the other elementary particles that exist on the low scale level of the
matter.
13.
References
1.
Fedosin S.G. Problems
of fundamental physics and possible ways of their solution // Cognition and
physical reality (Russian Journal), V. 9, No. 2, 2004, P. 34–
42.
2.
Jaakkola T., Moles M., Vigier J.-P.
Empirical Status in Cosmology and the Problem of the Nature of Redshifts //
Astronomische Nachrichten, 1979, Vol. 300, No. 5, P. 229–238.
3.
Fedosin S.G. Fizika
i filosofiia podobiia ot preonov do metagalaktik. – Perm,
Style - Mg, 1999, 544 pages. ISBN 5-8131-0012-1.
4. Fedosin
S.G. Sovremennye problemy fiziki: v
poiskakh novykh printsipov. – Moscow: Editorial URSS, 2002, 192
pages. ISBN 5-8360-0435-8.
5. Fedosin S.G. Electromagnetic
and Gravitational Pictures of the World. // Apeiron, Vol. 14, No. 4, P. 385-413, 2007.
6.
Fedosin S.G. Osnovy
sinkretiki: filosofiia nositeleĭ. – Moscow:
Editorial URSS, 2003, 464 pages. ISBN 5-354-00375-X.
7.
Hu, E.M, et al. A Redshift z = 6.56
Galaxy behind the Cluster Abell 370 // The Astrophysical Journal, 2002, Vol.
568, Issue 2, L. 75-79.
8.
Donald P. Schneider et al. The Sloan
Digital Sky Survey Quasar Catalog IV. Fifth Data Release. –
arXiv: astro-ph / 0704.0806 v1, 05 Apr.
2007.
9.
Carol J. Lonsdale, Duncan Farrah and
Harding E. Smith. Ultraluminous
Infrared Galaxies. – arXiv: astro-ph / 0603031 v1, 1 Mar. 2006 .
10.
Tifft, W. G. Redshift Quantization –
A Review // Astrophysics and Space Science, 1995, Vol. 227, P. 25-39.
11.
Guthrie, B. N. G.; Napier, W. M.
Evidence for redshift periodicity in nearby field galaxies // Royal
Astronomical Society, Monthly Notices, Vol. 253, Dec. 1, 1991, P. 533-544.
12.
Karachentsev I.D., Chernin A. Islands at ocean of dark
energy. / The world of a science, 2006, 11, (Cosmology).
13.
Borge Nodland, John P. Ralston. Indication of
Anisotropy in Electromagnetic Propagation over Cosmological Distances. –
arXiv: astro-ph / 9704196 v1, 20 April. 1997.
14.
Adam G. Riess et al. Observational
Evidence from Supernovae for an Accelerating Universe and a Cosmological
Constant. – arXiv: astro-ph / 9805201 v1, 15 May. 1998.
15.
W. M. Wood-Vasey. Observational
Constraints on the Nature of Dark Energy: First Cosmological Results from the
ESSENCE Supernova Survey. – arXiv: astro-ph / 0701041 v1, 2 Jan. 2007.
16.
Wayne Hu, Scott Dodelson. Cosmic
Microwave Background Anisotropies // Annu. Rev. Astron. and Astrophys., 2002,
Vol. 40, P. 1–50.
17.
Baym G., Pethick Ch., Sutterland P.
The ground state of matter at high densities: equation of state and stellar
models // The Astrophysical Journal, 1971, Vol. 170, P. 306–315.
18.
Bloom J. S., Frail D. A., Kulkarni S. R.
GRB Energetics and the GRB
Hubble Diagram: Promises and Limitations. – arXiv:
astro-ph /0302210 v2, 26 May
2003.
19.
Infinite
Hierarchical Nesting of Matter // on the Wikiversity.
20. Комментарии к книге: Федосин С.Г. Физические теории и бесконечная вложенность материи.
Пермь, 2009-2011, 858 стр., Табл. 21, Ил.41, Библ. 293 назв. ISBN
978-5-9901951-1-0.
21.
"Seven-Year
Wilson Microwave Anisotropy Probe (WMAP) Observations: Sky Maps, Systematic
Errors, and Basic Results". nasa.gov. Retrieved
2010-12-02.
Source:
http://sergf.ru/rsen.htm