Нужен ли постулат о постоянстве скорости
света в специальной теории относительности?
С.Г. Федосин,
А.С. Ким
01.08.2001
Предлагается вариант обоснования специальной теории относительности, не
требующий постулата о постоянстве скорости света во всех инерциальных системах
отсчёта. В качестве исходного принципа постулируется существование хотя бы
одной изотропной системы отсчёта, в которой скорость волны не зависит от
направления. Последующее применение принципа относительности позволяет доказать
неизменность скорости волны в инерциальных системах отсчёта, вывести
соотношения специальной теории относительности и предположить возможность
существования эфира как среды, влияющей на
распространение электромагнитных волн.
PACS number: 03.30.+p
_________________________________________________________________
Содержание
1. Введение ( 1 ).
2. Основные уравнения (2).
3. Заключение (19).
Список литературы (20).
1. Введение
В
основе всех практически важных физических теорий лежит специальная теория
относительности (СТО), позволяющая пересчитывать результаты экспериментов из
одной инерциальной системы отсчёта в другую. Характерным случаем здесь является
наблюдение движущихся с постоянной скоростью объектов в лабораторной системе
отсчёта. Соотношения СТО были выведены
Эйнштейном [1] в предположении
полной эквивалентности инерциальных систем отсчёта, что включает в себя
принцип относительности (изменение состояния движения наблюдателя и
регистрируемых им объектов не изменяет для наблюдателя видимую картину
явлений), и принцип постоянства скорости света. Кроме этого, были использованы
симметрии относительно сдвигов и поворотов в пространстве и времени Евклида.
Математически связь между
событиями в инерциальных системах отсчёта записывается с помощью преобразований
Лоренца. В настоящее время лоренц-инвариантность считается одним из главных
атрибутов каждой новой физической теории. Однако один из основных принципов СТО
– принцип постоянства скорости света во всех инерциальных системах отсчёта – до
сих пор остаётся одним из самых интригующих моментов теории. Одной из задач
настоящей работы как раз и является вывод данного постулата СТО из других
принципов. Вначале мы предполагаем, что существует хотя бы одна система отсчёта
настолько симметричная, что в ней скорость распространения волны в любом
направлении одинакова. После применения принципа относительности к объектам
этой системы отсчёта получается совокупность уравнений, решение которых
приводит к заключению о постоянстве скорости волны и её независимости от
направления распространения в инерциальных системах. В результате мы не
только выводим формулы СТО, но и обосновываем возможность существования эфира
как среды, связанной с распространением электромагнитных волн и вероятно
ограничивающей их скорость. Заметим, что все дальнейшие рассуждения приводят к
универсальным соотношениям, поскольку никак не связаны с конкретным типом
волны.
2. Основные уравнения
Пусть
имеется изотропная система отсчёта 
, в которой скорость гребня сферической волны одинакова по
всем направлениям и равна 
. Рассмотрим такую ситуацию, когда приёмник и источник
двигаются с разными скоростями в , а мы знаем только относительную скорость движения между
ними. На рисунке 1 наблюдатель находится в точке 
системы отсчёта 
, связанной с приёмником, а источник удаляется со скоростью 
относительно
приёмника из точки 
.
Рис. 1. Приёмник покоится в , источник двигается из в
, 
- скорость волны.
После
испускания первого гребня в точке источник за время 
по часам приёмника
перемещается в точку , где появляется второй гребень волны. Первый гребень за
время проходит расстояние 
со скоростью волны , так что расстояние между гребнями равно 
:
Разделив
на скорость гребней
волны , найдём время 
между попаданием
гребней в приёмник по его собственным часам. Из-за движения источника
относительно его собственное время
отличается от времени в . Введём коэффициент пересчёта 
, зависящий от скорости часов в , для определения собственного
времени этих часов. Тогда собственный период волны источника 
из-за движения
источника отличается от наблюдаемого в периода на некоторый
коэффициент :
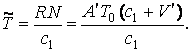(1)
На
рисунке 2 показана ситуация как на рисунке 1, но уже в изотропной системе
отсчёта , для наглядности пространственно совпадающие оси 
и 
разнесены.
Рис. 2. Система отсчёта 
двигается со скоростью
вдоль оси , приёмник находится в , источник двигается из в 
со скоростью 
относительно вдоль оси .
В
изотропной системе отсчёта скорость волны
равна . За время 
первый гребень из достигает точки 
, приёмник перейдёт в положение 
, а источник перемещается в , где появляется второй гребень:
Далее
в течении времени 
гребни синхронно
двигаются навстречу приёмнику, выдерживая между собой расстояние 
, равное 
. Встреча приёмника с первым гребнем произойдёт в точке 
:
После
встречи с первым гребнем в точке приёмник за время 
пройдёт расстояние 
, прежде чем
встретится со вторым гребнем в точке 
. Соответственно, второй гребень за время пройдёт
расстояние 
:
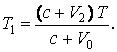
Времена
и в последнем равенстве
отсчитываются по часам в . Из-за движения источника и
приёмника относительно их собственные времена
отличаются от времени в . Перейдём к собственным значениям периодов времени с помощью
коэффициентов пересчёта времени 
и 
, зависящих от скоростей
и соответственно:
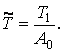(2)
Собственные
значения периодов между попаданием
гребней в приёмник (1) и (2) должны
совпадать, что даёт следующее равенство:
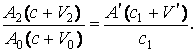(3)
Очевидно,
что коэффициент согласно (3)
существенно зависит от скорости волны ,
определяемой в системе отсчёта . Если скорости и равны и направлены в
одну сторону, то и приёмник и источник двигаются в с одинаковой
скоростью, и по (3) будет 
, 
. Это значит, что наблюдатель в не замечает изменения
периода или частоты волны от источника независимо от скорости движения системы
отсчёта в . Поскольку при этом за единицу
времени в и источник и приёмник
перемещаются на одинаковое расстояние, то и наблюдатель в отметит равенство
периода волны от источника и периода попадания гребней в приёмник. В
соответствии с принципом относительности физические явления в покоящихся или
движущихся с постоянной скоростью инерциальных системах отсчёта протекают одинаково,
а физические законы неизменны. Для случая электромагнитных волн также остаётся
неизменной энергия фотонов 
,
где 
- постоянная Планка, 
- частота. Вероятно, именно
принцип относительности и независимость внутренних физических явлений от
скорости системы отсчёта и послужили теми аргументами, на основании которых А.
Эйнштейн предложил свой постулат неизменности скорости света в любой
инерциальной системе отсчёта и как следствие вывел СТО [1]. Возвратимся теперь к (3) и предположим, что 
, как это было принято в [1]. Нетрудно проверить, что если
подставить в (3) следующие выражения:
(4)
то
соотношение (3) при условии выполняется
тождественно. При этом формулы (4) представляют нам характерные особенности СТО
– первая из них осуществляет преобразование лоренцевского множителя, а вторая
есть формула сложения скоростей в СТО.
Итак, формулы СТО (4) и
соотношение (3), фактически базирующееся на предположении о существовании
изотропной системы отсчёта , хорошо сочетаются друг с другом. Предположим теперь, что
изотропность системы отсчёта обеспечивается тем,
что в ней покоится эфир как некоторая среда, влияющая на распространение
электромагнитных колебаний. Тогда факты постоянства скорости света и
независимости скорости света от скорости источников легко можно было бы
объяснить, сославшись на внутренние свойства эфира, а СТО и эфир никак бы не
противоречили друг другу. Однако для полного признания
возможности существования эфира следует по меньшей мере доказать, что
действительно в ситуации на рисунке
1, то есть скорость волны для любого наблюдателя
в , движущегося относительно , остаётся равной скорости волны в изотропной системе
отсчёта . Оказывается, что постулат постоянства скорости света в
инерциальных системах отсчёта, на котором основана СТО, действительно может
быть выведен в рамках нашего подхода.
Для
этого вернёмся к рисунку 1 и переставим в нём приёмник и источник местами.
Теперь на рисунке 3 в точке находится источник, а
приёмник удаляется со скоростью вдоль оси .
Рис. 3. Источник покоится в , приёмник двигается из в
, 
- скорость волны вдоль оси .
В
отличие от ситуации на рисунке 1 сейчас гребни волны идут не против оси , а должны догонять приёмник,
двигаясь вдоль оси с некоторой скоростью . За время 
первый гребень
проходит расстояние 
, а приёмник перемещается из в 
:
Поскольку
в источник покоится,
расстояние между соседними гребнями волны равно 
, где - собственный период источника. Когда первый гребень
догнал приёмник в точке , второй гребень находился в , так что 
. Через время 
после этого второй
гребень настигает приёмник в точке , так что можно записать:
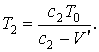
Переведём
промежуток времени в собственное время
приёмника 
. Для этого можно использовать тот же самый коэффициент из (1), который
связывает интервалы времени покоящихся и двигающихся в
часов:
(5)
Теперь определим время 
между
приходом двух последовательных гребней в приёмник с точки зрения изотропной
системы отсчёта в соответствии с
рисунком 4.
Рис. 4. Система отсчёта двигается со скоростью
вдоль оси , источник находится в , приёмник двигается из в 
со скоростью относительно вдоль оси .
За
время 
приёмник перемещается
из в , первый гребень волны от источника пройдёт расстояние 
со скоростью ,
а сам источник за это же время дойдёт до точки 
и там появится второй
гребень. Расстояние между гребнями будет 
:
Пусть
далее за время 
первый гребень
проходит путь 
и настигает приёмник в
точке 
, а второй гребень при этом находится в 
, так что можно записать:
Встреча
второго гребня с приёмником произойдёт через время 
в точке :
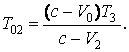
Переведём
интервалы времени и , отсчитываемые в , в собственные интервалы для
испускания волны источником и для приёма гребней приёмником соответственно с
помощью коэффициентов и :
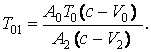
Сравнение
данной величины со значением (5) даёт:
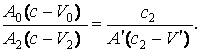(6)
Соотношения (3), (6) являются двумя уравнениями для пяти
неизвестных величин , 
, , , . Прежде чем найти необходимое для дальнейшего решения третье
уравнение, рассмотрим зависимость длины тела вдоль оси от его скорости в
системе отсчёта . Процедура измерения длины покоящегося тела заключается в
следующем: от одного конца тела к другому пускается волна, которая отражается и возвращается
обратно через некоторое время 
. Под длиной тела 
в этом случае
подразумевается величина 
, где 
скорость волны. На
рисунке 5 показано движущееся в тело, на одном его
конце в точке находятся источник и
приёмник волны, а на другом конце в точке установлен отражатель.
При движении тела отражатель в точке убегает от волны, что
увеличивает время встречи волны с отражателем от величины 
до 
:
Рис. 5. Движущееся со скоростью 
тело длиной 
по мере движения
переходит в положение 
.
Мы
предполагаем, что длина движущегося тела
сама по себе остаётся
неизменной при любом движении как у твёрдого тела, но отличается от длины
покоящегося тела вследствие процедуры
измерения длины движущегося тела с помощью волны. Через время 
после отражения в
положении 
волна возвращается
обратно и встречается с приёмником в положении 
:
Суммируя
времена 
и 
, найдём промежуток времени 
, который также как периодический процесс излучения волны
может быть связан с промежутком времени 
в собственной системе
отсчёта движущегося тела с помощью коэффициента 
:
(7)
С точки
зрения движущейся относительно с постоянной скоростью
системы отсчёта на рисунке 5 длина тела
должна равняться её
значению в , то есть величине . В самом деле, при переходе в от покоящегося тела к
движущемуся его длина согласно измерениям изменится и далее останется
неизменной благодаря постоянству скорости, но точно также изменится и масштаб
длины на движущемся теле. Следовательно, длина покоящегося в тела имеет столько же
масштабных единиц длины , сколько содержится в длине покоящегося в этого же тела
масштабных единиц длины . В волна
при движении вдоль оси имеет скорость , как на рисунке 3, а при движении против оси её скорость равна в соответствии с
рисунком 1. Тело длиной 
неподвижно
относительно , и для времени движения волны от до и обратно по часам в имеем:
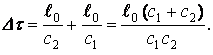(8)
Но что можно сказать о
времени ? Мы знаем, что показания движущихся относительно часов отличаются от
показаний часов, покоящихся в . Поскольку и и
тело синхронно двигаются
относительно , то часы системы отсчёта и световые часы на
отрезке с периодом должны в одинаковой
степени изменить свой ход относительно . Это означает, что длительность относительно часов
в такая же, как и
длительность относительно часов
в . Следовательно, в
данном случае в не только , но и 
. Отсюда с помощью (8) и (7) получаем следующее:
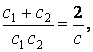(9)
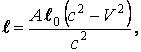(10)
то
есть длина движущегося в тела вдоль направления
движения изменяется вследствие выбранной нами процедуры измерения хода часов и
длин тел непосредственно с помощью волны.
Преобразуем теперь уравнения
(3), (6), (9). Из (9) выражаем , перемножаем (3) и (6), подставляем в результат и находим вначале , а затем и отношение
скоростей 
:
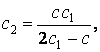
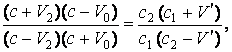
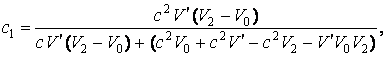
(11)
Скорости волны против оси и вдоль оси в системе отсчёта не должны зависеть от
скорости движущихся в тел. В том частном
случае, когда , тело покоится в , а его скорость относительно равна скорости
движения системы отсчёта относительно . Тогда из (11) следует, что при 
величина 
, а отношение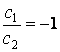 
. Поскольку отношение скоростей волны не может быть
отрицательным, нам следует признать, что
в (11) 
. Данное условие даёт формулу
сложения скоростей в СТО, аналогичную (4):
(12)
Кроме
этого, при в (11) получается 
. Тогда из (9) находим 
, то есть скорости волны против и вдоль оси в одинаковы и равны
скорости волны в изотропной системе отсчёта . Разделив (3) на (6), при
условии получим:
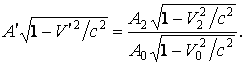(13)
Подстановка
(12) в (13) даёт: что также совпадает с
(4).
Поперечные размеры тел. Пусть в изотропной системе
отсчёта 
находится неподвижное
тело, размер которого в некотором направлении, перпендикулярном оси , равен 
. Поместим в точке 
источник и приёмник, а
в точке - отражатель волны, и пустим волну из в и обратно. Если засечь
время , необходимое для движения волны вперёд и назад, то ширина
покоящегося тела будет равна:
(14)
Переведём
теперь данное тело в движение относительно оси
со скоростью , так что оно будет покоиться в сопутствующей системе отсчёта
на рисунке 6. При
движении тела 
волна через время 
после начала движения
встречается с отражателем в положении 
и далее возвращается в
приёмник в положении 
, затрачивая на это то же самое
количество времени . В качестве эффективной ширины движущегося тела примем
значение 
:
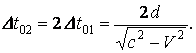
Время
движения волны 
отсчитывается по часам
в и может быть переведено в собственное время тела с помощью
коэффициента :
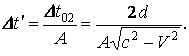
Как было
показано выше, длительности одинаковых процессов в собственных системах отсчёта
должны быть равны друг другу. Следовательно, 
,
и с учётом (14) имеем:
(15)
Рис. 6. Система отсчёта и тело двигаются со скоростью
вдоль оси системы отсчёта , движение волны по ломаной линии 
показано относительно .
Предположим, что в начальный момент, когда система отсчёта вместе с телом начала двигаться
относительно , за счёт движения как-то изменились масштабы длины осей , а также и размеры всех тел, неподвижных в . Мы также считаем, что движение относительно одинаково изменяет как
масштабные линейки в , так и соответствующие размеры любых тел. Другими словами, в
каждой инерциальной системе отсчёта , движущейся относительно , покоящиеся в тела должны иметь те же размеры,
какие они имели при покое в . Исходя из этого, на рисунке 6 в
системе отсчёта для тела с
шириной выполняется
соотношение:
причём в силу симметрии относительно движения вдоль оси волна в при движении из в и обратно имеет одну и
ту же скорость 
. Учитывая (14) и соотношение 
, приходим к равенству
, так что скорость волны в
поперёк оси равна скорости волны в
изотропной системе отсчёта .
Скорость волны в
произвольном направлении в системе отсчёта 
.
Пусть
в находится
неподвижное тело с размером 
вдоль оси и размером
поперёк оси , как показано на рисунке 7. Суммарное время для движения
волны из через точки и и обратно в равно:
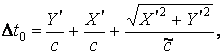(16)
причём
скорость волны вдоль и поперёк оси равна в соответствии с
полученными выше результатами, а при движении по диагонали 
скорость волны равна
некоторой величине 
.
Рис. 7. Волна выходит из , отражается в и в и по диагонали 
возвращается обратно в
.
Рассмотрим
ситуацию рисунка 7 с точки зрения системы отсчёта . На рисунке 8 система отсчёта вместе с телом,
имеющим в размеры 
и 
, двигается со скоростью
вдоль оси . За время 
волна пройдёт путь 
,
а точка переместится в
положение 
:
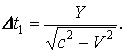
Далее
за время точка из положения 
переходит в положение 
и встречается там с
волной, идущей из
:
Затем
по истечении времени 
волна встречается с
точкой в положении 
:
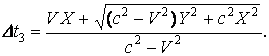
Рис. 8.
За счёт движения системы отсчёта вдоль оси системы отсчёта движение волны
происходит по ломаной линии 
.
В
соответствии с (10) для длины тела вдоль оси имеем: 
, в то время как поперечные размеры в
согласно (15) будут
таковы: 
Подставляя
значения 
и 
, находим период времени в :
Если
перевести наблюдаемый в период 
в собственное время
движущегося тела с помощью коэффициента , то полученный результат можно будет сравнить с (16):
что
даёт равенство 
при любых и , и значит скорость волны одна и та же для всех возможных
направлений движения волны в .
Таким образом, при оценке с
помощью волн параметров тел, движущихся с постоянной скоростью вдоль оси
наблюдения, мы приходим к постоянству скорости волны относительно каждого
такого тела, а также к формулам СТО. В данном случае условие 
в инерциальных
системах отсчёта делает их симметричными по отношению друг к другу и к
изотропной системе отсчёта . Отсюда следует ожидать, что коэффициент должен иметь один
и тот же вид во всех инерциальных
системах отсчёта. Если обозначить: 
, где 
и 
являются функциями
скорости , то из (13) следует:
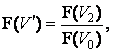(17)
причём
каждый из коэффициентов 
в (13) зависит соответственно только от скоростей 
, а сами скорости связаны формулой (12): 
В
случае, когда 
, а значит 
, из (17) получаем 
. При 
из формулы сложения
скоростей следует 
и согласно (17) 
при любом . Наконец, если 
, то 
, 
, и по (17)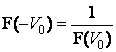 
. Очевидно, что всем этим требованиям удовлетворяет простейшая
функция вида:
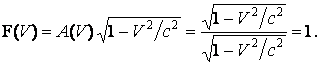
Отсюда
находим зависимость коэффициента 
от скорости движения в
инерциальной системе отсчёта:
(18)
Эффект
замедления времени (7) в движущемся относительно наблюдателя теле в явном виде
с учётом (18) можно записать так:
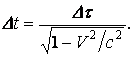(19)
Формулы
(10) и (15) для длины и ширины тела относительно скорости его движения
принимают теперь обычный для СТО вид:
(20)
Как
показано в [2], соотношения (18) вполне достаточно, чтобы вывести
преобразования Лоренца и все остальные следствия СТО.
3. Заключение
Исходя
из вышеизложенного, основные результаты специальной
теории относительности могут быть получены на основе следующих предположений:
1.
Выполняется принцип относительности.
2.
Существует изотропная система отсчёта, в которой скорость волны одинакова по
всем направлениям.
3.
Процедура измерения пространственно-временных параметров тел осуществляется
непосредственно с помощью самой волны.
Тогда
постулат о постоянстве скорости света в инерциальных системах оказывается
вторичным и может быть сам выведен в рамках нашего подхода. Предположение об
изотропной системе отсчёта естественным образом сочетается с покоящимся в этой
системе отсчёта эфиром, который и обеспечивает изотропию свойств волны. Однако
свойства эфира в движущихся с постоянной скоростью системах отсчёта не
проявляются, что является следствием использования нами принципа
относительности, соответствующей процедуры измерений и вытекающей отсюда
относительной эквивалентности инерциальных систем отсчёта.
Необходимо сделать ещё одно
замечание, касающееся измерений в инерциальных системах отсчёта. Часто
случается так, что скорость движения тел не совпадает по направлению с линией
наблюдения за телом. В то же время сделанные выше выводы были справедливы для
движения тел вдоль линии наблюдения. В данном случае нужно учесть, что все
точки любой конкретной системы отсчёта должны быть синхронизированы между
собой. Поэтому, если эффект замедления времени отмечается вдоль линии
наблюдения хотя бы в одной точке системы отсчёта, то точно такой же эффект
должен быть обнаружен и в остальных точках, включая центр системы отсчёта,
независимо от направления скорости тела относительно этого центра. Если эффект
замедления времени в движущемся теле носит абсолютный характер, то эффект
сокращения длины тела по (20) является относительным, так как зависит от
ориентации скорости тела и линии наблюдения.
Список литературы
1. Эйнштейн А Собрание научных трудов. Т.1. (М.:
Наука, 1965)
2. Федосин С Г Физика и философия подобия от преонов до
метагалактик. (Пермь: Стиль-МГ, 1999)
Источник:
http://sergf.ru/pos.htm