Поляризуемость

Материал из свободной русской энциклопедии «Традиция»

Поляризуемость есть свойство возникновения в некотором распределении электрических зарядов (у элементарных частиц, атомов, ионов, молекул) наведённого дипольного электрического или (и) магнитного моментов под действием внешнего электромагнитного поля. Понятие поляризуемости имеет наибольшее значение в физике элементарных частиц, в молекулярной физике и в химии, при изучении диэлектриков и намагничивающихся материалов, при исследовании оптических эффектов в веществе, а также для учёта межчастичных и межмолекулярных взаимодействий.

Содержание

1 Электрическая поляризуемость

1.1 Особенности в разных системах

2 Магнитная поляризуемость
3 Примечания
4 См. также

Электрическая поляризуемость

Электрическая поляризуемость $~\alpha$ определяется как коэффициент пропорциональности между напряжённостью приложенного электрического поля $~\boldsymbol{E}$ и получающимся наведённым электрическим дипольным моментом частицы $~\boldsymbol{D}$ в формуле для системы физических единиц СИ:

$~\boldsymbol{D} = 4\pi \varepsilon_0 \alpha \boldsymbol{E},$

где $~\varepsilon_0$ - электрическая постоянная.

Если моделировать начальную конфигурацию распределения зарядов в виде нейтральной хорошо проводящей тонкостенной пустотелой сферы, либо в виде нейтрального в целом шара, то можно показать, что $~\alpha$ равно кубу радиуса этой сферы (шара). ^[1] Отсюда следует, что размерность $~\alpha$ есть м³, совпадая с размерностью объёма.

Особенности в разных системах

Как правило, линейная зависимость между приложенным электрическим полем и возникающим дипольным моментом справедлива лишь в слабых полях, при усилении поля линейность пропадает. В некоторых веществах направления векторов $~\boldsymbol{E}$ и $~\boldsymbol{D}$ могут не совпадать. В таком случае поляризуемость $~\alpha$ рассматривается уже не как скалярная величина, а как тензор второго ранга, содержащий 9 компонент в виде 3 $\times$ 3 матрицы.

При измерении дипольного момента в системе из многих частиц следует учитывать, что результирующее электрическое поле, действующее на отдельную частицу, является суммой внешнего приложенного поля и усреднённого электрического поля от остальных частиц. Последнее поле включает в себя постоянную компоненту, не зависящую от внешнего поля, и наведённую внешним полем компоненту.

Различают статическую и динамическую поляризуемости. Первая связана с приложением постоянного электрического поля, а вторая – с переменным электрическим полем. В веществе возможны эффект задержки установления дипольного момента по отношению к началу действия электрического поля, сдвиг фазы между дипольным моментом и приложенным переменным электрическим полем, зависимость значения амплитуды поляризуемости от частоты изменения поля вплоть до уменьшения до нуля. Соответственно, наблюдаются такие явления, как дисперсия (зависимость от частоты), а также поглощение энергии электрического поля посредством резонансного взаимодействия запаздывающего наведённого дипольного момента с полем, и посредством сдвига диполей при ориентационной поляризации.

В зависимости от исследуемых объектов измеряют:

поляризуемость у отдельных элементарных частиц. Примером является значение 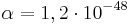$~\alpha=1,2\cdot 10^{-48}$ м³ для протона. ^[2]
электронную поляризуемость за счёт сдвига электронов в оболочках атомов.
ионную поляризуемость при сдвиге в противоположных направлениях разноимённых ионов в ионных кристаллах.
атомную поляризуемость вследствие смещения атомов в молекулах.

На практике измеряют обычно поляризацию среды, понимаемую как дипольный электрический момент единицы объёма среды. Разделив поляризацию среды на концентрацию диполей, находят дипольный момент одной частицы и затем её поляризуемость в приложенном электрическом поле. Между поляризуемостью, абсолютной диэлектрической проницаемостью и диэлектрической восприимчивостью разных сред существуют взаимосвязи, выражаемые, например, в соотношении Клаузиуса–Мосотти. [2]

Магнитная поляризуемость

Магнитная поляризуемость $~\beta$ определяется как коэффициент пропорциональности между индукцией приложенного магнитного поля $~\boldsymbol{B}$ и наведённым дипольным магнитным моментом частицы $~\boldsymbol{ P_{\mu}}$ в формуле для системы физических единиц СИ:

$~\boldsymbol{P_{\mu}} = \frac {4\pi \beta \boldsymbol{B}}{\mu_0},$

где $~\mu_0$ - магнитная постоянная.

Для оценки размерности магнитной поляризуемости удобно рассмотреть дипольный магнитный момент маленькой петли с нулевым электрическим сопротивлением, возникающий при помещении её в магнитное поле за счёт эффекта электромагнитной индукции. Если радиус петли , а наведённый ток электронов , то магнитный момент будет равен $~ P_{\mu}=I \pi r^2$ . В этом случае магнитная поляризуемость будет равна кубу радиуса петли, умноженному на отношение двух энергий – кулоновской энергии электрона в поле движущихся зарядов тока в петле, и удвоенной энергии покоя электрона. Следовательно, в обычных условиях при малых токах величина магнитной поляризуемости будет значительно меньше куба радиуса магнитного диполя, имея при этом размерность м³. Для протона $~\beta=1,9\cdot 10^{-49}$ м³, что согласуется с электрической поляризуемостью протона. ^[1]

Основные особенности магнитной поляризуемости повторяют особенности для электрической поляризуемости, с заменой электрических величин на соответствующие магнитные величины. По своему смыслу к магнитной поляризуемости близка магнитная восприимчивость, связывающая намагниченность (дипольный магнитный момент единицы объёма) среды и напряжённость приложенного магнитного поля.

Примечания

^а ^б Комментарии к книге: Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
Yao W.-M. et al., (Particle Data Group), Physics Letters, Vol. B667, P. 1 (2008) and 2009 partial update for the 2010 edition. [1]

См. также

Поляризация диэлектриков
Магнитная восприимчивость

Источник: http://sergf.ru/po.htm

На список страниц